激活函数：项目匹配秘籍——选择适合你的那一个激活函数

# 1. 深度学习中的激活函数概述

## 1.1 激活函数的概念与作用

在深度学习模型中，激活函数是神经元输出与输入关系的非线性映射，其核心作用是引入非线性因素，使神经网络能够学习和模拟复杂的函数。没有激活函数，无论多少层的神经网络，其输出都等同于一个线性模型，这极大地限制了模型的表达能力。

## 1.2 激活函数的重要性

激活函数的选择直接影响到深度学习模型的训练效率、模型性能以及最终结果的准确性。它们在前向传播中决定着信息的流动方式，在反向传播中则是计算梯度的关键部分。因此，选择合适的激活函数，对于神经网络的优化和泛化能力具有决定性的作用。

## 1.3 常用激活函数类型

目前深度学习中常用的激活函数包括Sigmoid、Tanh、ReLU系列等。这些函数各有特点，在不同类型的网络架构和任务中表现出不同的性能。本章后续将对这些常见激活函数进行详细的理论分析，阐述它们在实际应用中的表现和适用场景。

# 2. 常见激活函数的理论分析

激活函数在深度学习中扮演着至关重要的角色，它决定了神经网络能否有效地学习复杂模式。本章将详细探讨几种常用的激活函数，包括它们的定义、数学基础、优缺点以及相互之间的比较。通过理论分析，我们可以更好地理解这些函数如何影响神经网络的性能和训练过程。

## 2.1 Sigmoid函数及其变体

### 2.1.1 Sigmoid函数的定义和数学表达

Sigmoid函数，也称为逻辑函数，是深度学习中最早使用的激活函数之一。它的数学表达式如下：

\sigma(x) = \frac{1}{1 + e^{-x}}

该函数将任意实数值压缩到(0, 1)的范围内，因此常用于输出层，尤其是当任务是二分类问题时。Sigmoid函数的图形呈现出典型的S形状，这也是它名称的由来。

### 2.1.2 Sigmoid函数的优缺点分析

Sigmoid函数的一个显著优点是它的输出可以被解释为概率，这在处理分类问题时非常有用。然而，它也有几个缺点：

- 梯度消失：当输入值远离零点时，Sigmoid函数的梯度趋近于零，导致在深层网络中学习效率低。
- 输出不是零中心的：这会导致梯度下降过程中遇到不必要的困难。
- 计算开销大：由于涉及到指数计算，Sigmoid函数在计算上比线性函数或其他激活函数复杂。

## 2.2 Tanh函数

### 2.2.1 Tanh函数的数学基础

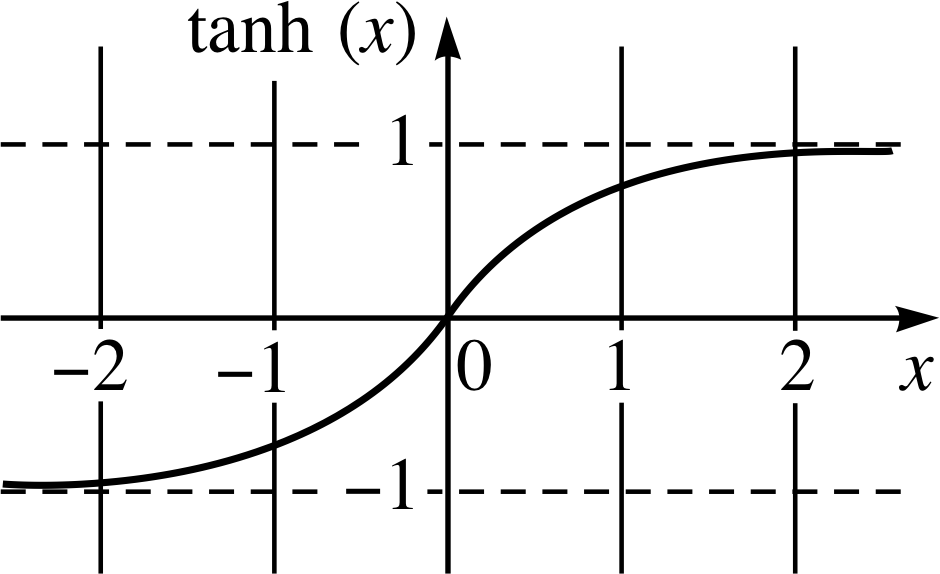
双曲正切函数（Tanh）是Sigmoid函数的变体，其数学表达式为：

\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}

Tanh函数与Sigmoid函数相似，但它将输入压缩到(-1, 1)的范围内，输出为零中心，这有助于缓解梯度消失的问题。

### 2.2.2 Tanh与Sigmoid的比较

Tanh函数和Sigmoid函数在很多方面都很相似，但也有以下区别：

- 输出范围：Tanh的输出范围是(-1, 1)，而Sigmoid是(0, 1)，这意味着Tanh更容易让数据在零点附近，这有助于缓解非零中心输出的问题。
- 梯度：虽然两者都会遇到梯度消失问题，但Tanh的梯度比Sigmoid的梯度要大，这使得Tanh在很多情况下是一个更好的选择。

## 2.3 ReLU函数系列

### 2.3.1 ReLU函数的起源和特点

Rectified Linear Unit（ReLU）函数是在2011年被提出的一种激活函数。它解决了Sigmoid和Tanh的梯度消失问题。ReLU函数的表达式为：

f(x) = max(0, x)

ReLU函数只在正数部分激活，因此它能保持稀疏性，有助于缓解过拟合问题，并且计算效率高。

### 2.3.2 Leaky ReLU和Parametric ReLU

Leaky ReLU和Parametric ReLU是ReLU的扩展，它们试图解决ReLU在负区间梯度为零的问题。

- Leaky ReLU：在负区间允许一个很小的非零斜率，表达式通常为：

f(x) = \begin{cases} 
x & \text{if } x \geq 0 \\
\alpha x & \text{if } x < 0
\end{cases}

- Parametric ReLU（PReLU）：与Leaky ReLU类似，但斜率α是一个可通过学习优化的参数：

f(x) = \begin{cases} 
x & \text{if } x \geq 0 \\
\alpha x & \text{if } x < 0
\end{cases}

Leaky ReLU和PReLU通过允许负值的激活，从而在一定程度上解决了ReLU的“死亡ReLU”问题。

## 2.4 其他激活函数

### 2.4.1 Swish和Softplus的特性

Swish和Softplus是近年来提出的两种新激活函数，它们试图结合ReLU和Sigmoid的优点。

- Swish函数：由Google提出，其表达式为：

f(x) = x \cdot \sigma(x)

Swish函数没有数学上的解析形式，需要通过数值方法计算。

- Softplus函数：可以被视为ReLU的平滑版本，表达式如下：

f(x) = \log(1 + e^x)

Softplus函数在理论上可以保证输出的正性，与ReLU相比，它在负区间有非零导数，但计算成本更高。

### 2.4.2 激活函数的选择标准

选择激活函数时应该考虑以下因素：

- 数据分布：激活函数的选择应该基于输入数据的特性。
- 网络结构：深度和宽度也会影响激活函数的选择。
- 任务类型：不同的任务可能需要不同的激活函数。
- 计算效率：资源有限时，计算成本是一个重要的考虑因素。

通过这些标准，可以更好地在实践中选择合适的激活函数来优化深度学习模型的性能。

# 3. 激活函数在项目中的应用实践

## 3.1 激活函数在分类任务中的应用

### 3.1.1 Sigmoid和Softmax在多分类中的角色

在多分类问题中，模型需要将输入数据分配给两个以上的类别。Sigmoid函数在二分类问题中非常有用，因为它可以将输出压缩到(0,1)区间，表示概率值。然而，对于多分类问题，我们通常会使用Softmax函数，它是Sigmoid函数在多维情况下的扩展。

Softmax函数将一个固定大小的实数向量转换为概率分布。其数学表达式如下：

\[ \text{Softmax}(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} \]

其中，\( \mathbf{z} \) 是输入向量，\( e \) 是自然对数的底数，\( K \) 是类别数。

Softmax函数的主要优势在于它能够为每个类别生成一个概率值，且这些概率值加起来等于1，从而直观地表示每个类别的相对概率。

import numpy as n