【递归技巧探秘】：打造优雅递归函数的艺术

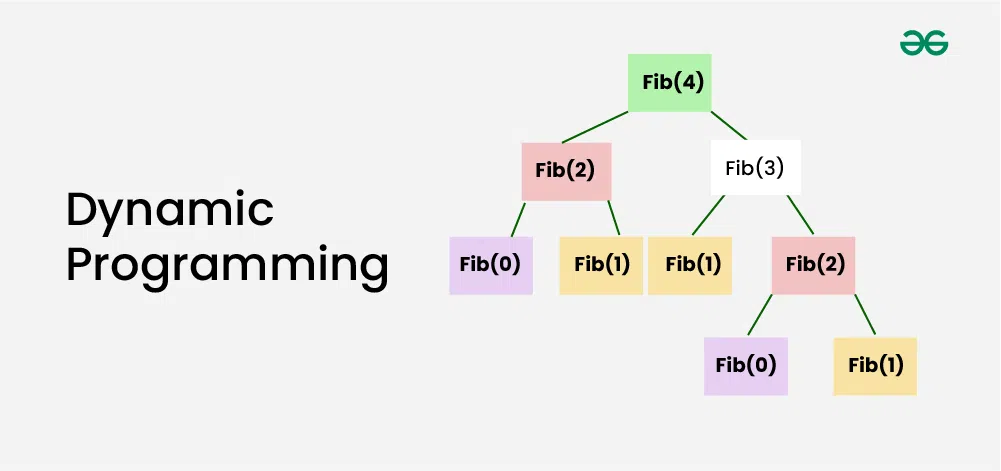
# 1. 递归函数的艺术与魅力

递归函数，作为计算机科学中的一个核心概念，不仅仅是一种编程技巧，它更像是一种艺术，能够以简洁而优雅的方式解决复杂问题。在这一章中，我们将探索递归的神秘面纱，了解它如何让代码更加简洁，以及它是如何在各种场景下展现其艺术与魅力的。

## 1.1 递归的魅力所在

递归的魅力在于它的简洁性和表达力。通过递归，复杂的算法能够被分解为更小的、可重复的子问题。这种方法特别适合解决那些具有天然递归性质的问题，比如树形结构的遍历或分治算法。递归的实现通常只需要很少的代码行数，但却能够展现出强大的计算能力。

def factorial(n):
    if n == 1:
        return 1
    else:
        return n * factorial(n-1)

以上是一个简单的阶乘计算函数，它展示了递归如何一步步逼近最终结果。

## 1.2 递归的思考方式

递归的思考方式要求我们跳出传统的迭代模式，转而采用自顶向下的思维方式。它要求我们识别并定义问题的子问题，这些子问题与原问题具有相同或类似的结构。学会这种思维方式能够帮助我们更好地理解和设计算法，尤其是在处理递归数据结构时。

递归的艺术与魅力在于它的简洁与力量，通过后续章节的深入探索，我们将更全面地理解这一概念的深度与广度，以及它在不同领域中的应用与挑战。

# 2. 递归理论基础

### 2.1 递归的基本概念

#### 2.1.1 递归的定义和原理

递归是一种在函数定义中出现函数自身调用的技术。它是计算机编程中一种强大的方法，可以将复杂问题简化为相似的小问题，直至解决。

递归函数通常包含两个部分：基本情况和递归步骤。基本情况是递归结束的条件，是不需要递归调用的最简单情况。递归步骤则是函数调用自身以解决更小的子问题。

递归的原理可以用数学归纳法理解，即先证明基本情况成立，然后假设对某个规模的问题递归能正确处理，进而证明它能处理更大规模的问题。

下面用伪代码展示一个递归函数定义的通用结构：

function recursiveFunction(parameters) {
    if (basicCondition) {
        // 基本情况处理
        return result;
    } else {
        // 递归步骤，调用自身
        return recursiveFunction(modifiedParameters);
    }
}

#### 2.1.2 递归与迭代的比较

递归和迭代都是编程中常用的重复执行指令的方法，但它们在执行方式和效率上有所差异。迭代通常使用循环结构如for或while，而递归则通过函数调用自身实现。

递归通常更直观，代码更简洁，但可能导致额外的开销，如重复计算和调用栈溢出。迭代则容易理解且效率高，但有时代码较为复杂。

从逻辑上讲，任何递归算法都可以用迭代重写，反之亦然，但在实际应用中，选择哪种方法取决于具体问题的性质和求解效率。

### 2.2 递归函数的工作机制

#### 2.2.1 调用栈和内存管理

当函数调用自身时，系统需要记住函数当前的执行状态，这涉及到调用栈（call stack）的概念。调用栈是一个记录函数调用历史的栈结构，用于跟踪函数执行的位置，保存局部变量和参数。

在递归中，每次递归调用都会在调用栈上增加一层，这可能导致栈溢出。因此在设计递归函数时，必须确保递归有终止条件，避免无限递归。

// 调用栈示例伪代码
stack.push(callFrame); // 将当前调用帧加入栈
stack.pop(); // 从栈中移除当前调用帧，返回到上一层

#### 2.2.2 递归终止条件的设计

设计递归函数时，终止条件是避免无限递归的关键。终止条件是函数不再继续递归调用的情况，通常对应于问题的最简单情况。

正确设计终止条件非常重要，否则可能会导致栈溢出错误。终止条件应简单明确，容易验证，并能确保每次递归调用都使问题规模向终止条件靠拢。

### 2.3 递归算法的分类和应用

#### 2.3.1 线性递归与树形递归

递归算法根据调用关系可以分为线性递归和树形递归。线性递归中，每次函数调用只产生一个递归调用；树形递归则会产生多个递归调用，形成类似树状的调用结构。

线性递归的典型例子是计算阶乘，而树形递归在计算斐波那契数列时显得特别明显，因为每个数列项是前两项之和。

// 阶乘计算示例（线性递归）
function factorial(n) {
    if (n <= 1) return 1;
    else return n * factorial(n - 1);
}

// 斐波那契数列计算示例（树形递归）
function fibonacci(n) {
    if (n <= 1) return n;
    else return fibonacci(n - 1) + fibonacci(n - 2);
}

#### 2.3.2 分治法、回溯法与递归

分治法和回溯法是两种常用的递归算法设计思想。分治法将问题分解为更小的子问题，分别解决后合并结果；回溯法则是一种试探和回溯的算法策略，尝试分步解决一个问题。

分治法的代表算法有快速排序和归并排序，而回溯法的经典例子是八皇后问题。

// 分治法快速排序示例伪代码
function quickSort(array) {
    if (array.length <= 1) return array;
    else {
        pivot = choosePivot(array);
        left = [];
        right = [];
        for (i = 1; i < array.length; i++) {
            if (array[i] < pivot) left.push(array[i]);
            else right.push(array[i]);
        }
        return quickSort(left).concat([pivot], quickSort(right));
    }
}

至此，我们已经探讨了递归理论的基础知识，这为深入理解递归算法的实现和优化打下了坚实的基础。在下一章中，我们将具体实现递归函数，并探索递归在编程中的多种应用。

# 3. 递归编程实践

## 3.1 简单递归函数的实现

递归函数是计算机科学中一种强大的编程范式，它允许函数调用自身来解决问题。在这一部分，我们将深入探讨如何实现简单的递归函数，包括计算阶乘和斐波那契数列。

### 3.1.1 计算阶乘的递归实现

阶乘函数（n!）是递归概念的经典入门案例。阶乘定义为一个正整数n所有小于或等于n的正整数的乘积，通常表示为n!。

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

上述代码是计算阶乘的简单递归实现。这里有几个关键点需要注意：

- 基准情况（Base Case）：`if n == 0: return 1`，这是递归停止的条件。在数学上，0的阶乘定义为1。
- 递归情况（Recursive Case）：`return n * factorial(n-1)`，这是函数调用自身的部分，它将问题分解为更小的子问题。

在实际应用中，递归函数需要明确基准情况，否则会导致无限递归，最终可能会引发栈溢出错误。

### 3.1.2 斐波那契数列的递归解法

斐波那契数列是由0和1开始，后面的每一项数字都是前两项数字的和。斐波那契数列的前几项是：0, 1, 1, 2, 3, 5, 8, 13, ...

def fibonacci(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci(n-1) + fibonacci(n-2)

斐波那契数列的递归实现同样依赖基准情况来停止递归。然而，与阶乘不同的是，斐波那契数列递归解法在n较大时会引发性能问题。这是因为相同子问题的重复计算，时间复杂度会随着n的增加呈指数级增长。

## 3.2 复杂递归问题的解决方案

在复杂问题中，递归提供了一种优雅的解决方案。下面，我们将以汉诺塔问题和二叉树遍历为例，讨论如何解决复杂递归问题。

### 3.2.1 汉诺塔问题的递归算法

汉诺塔问题是一个经典的递归问题，目标是将所有的盘子从一个柱子移动到另一个柱子上，过程中遵守以下规则：

- 每次只能移动一个盘子。
- 任何时候，在三个柱子中，较大的盘子不能叠在较小的盘子上面。

def hanoi(n, source, target, auxiliary):
    if n > 0:
        # 将 n-1 个盘子从源移动到辅助
        hanoi(n-1, source, auxiliary, target)
        # 将剩下的盘子从源移动到目标
        print(f"Move disk {n} from {source} to {target}")
        # 将 n-1 个盘子从辅助移动到目标
        hanoi(n-1, auxiliary, target, source)

在上述代码中，`hanoi`函数通过递归调用自己来处理盘子的移动。这里体现了一个分治策略，即将大问题分解成更小的子问题。递归算法的魅力在于它能够通过简单的步