递归与分形：自然界中的递归现象及其应用

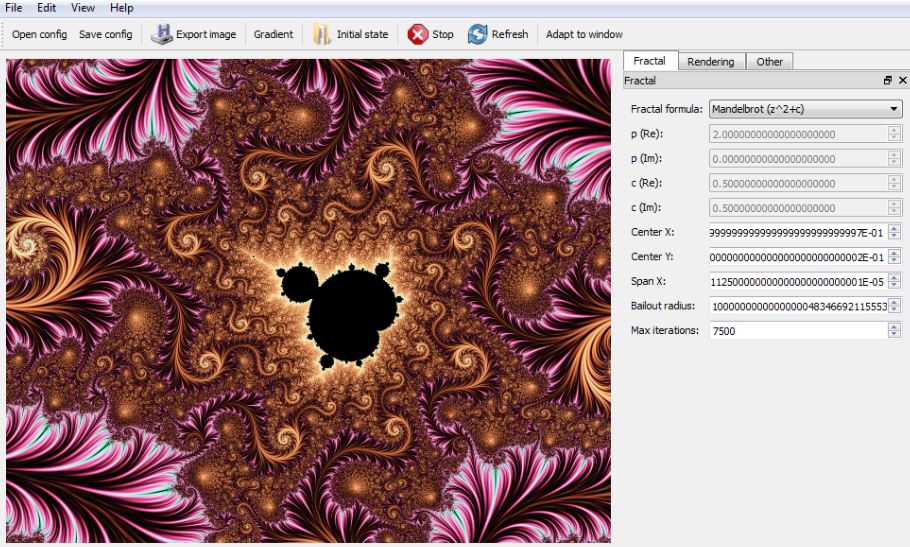
# 1. 递归现象的自然美

在自然界中，递归现象如同一张精细的画卷，无处不在地展示着它的美丽。它是一种自相似的模式，可以在不同的尺度上反复出现，这种现象不仅令人惊叹，而且是大自然的一种普遍语言。在这一章节，我们将探索递归在自然界的奇妙之处，从雪花的对称结晶到河流的分支结构，每个细节都蕴含着无限的复杂性和深邃的美。

## 1.1 自然界中的对称与模式

自然界中无处不在的对称性，从宏观的星系旋涡到微观的原子结构，都遵循着某种规律性的递归模式。例如，雪花的六角形晶体是通过递归法则不断重复形成的，这不仅遵循了物理规律，更展现了自然界的精细工艺。

## 1.2 递归与生命的和谐

递归不仅体现在无生命的自然现象中，生命体的生长过程也展示了这一现象。植物的生长模式，从一颗种子到一棵参天大树，都遵循着递归的生长法则。它不仅是自然选择的结果，更是生物适应环境的一种智慧表现。

通过上述内容，我们将进入一个由递归现象构建的奇妙世界，发现它在自然界中扮演的角色，并逐步揭开它背后的数学和物理原理。在接下来的章节中，我们将深入探讨递归的理论基础以及它在数学、生物学、地质学和艺术中的应用。

# 2. 递归理论基础与数学原理

## 2.1 递归的定义和类型

递归是计算机科学中的一个核心概念，其定义指的是一个函数直接或间接地调用自身。递归的这种自我引用特性，让它成为表达复杂问题的一种强大工具。然而，递归并非计算机科学所独有，数学上也有丰富的递归理论和应用。

### 2.1.1 线性递归和非线性递归

在递归中，根据递归函数调用自身时参数变化的不同，可以分为线性递归和非线性递归两种类型。

线性递归是一种参数线性变化的递归，例如阶乘函数的实现。每个递归调用仅产生一个后续调用，形式如下：

F(n) = n * F(n - 1) if n > 1
F(1) = 1

非线性递归是指递归函数在每次调用时产生多个后续调用。一个典型的例子是计算斐波那契数列，它在第`n`个位置上的数是前两个数之和。

代码示例：

def factorial(n):
    if n == 1:  # 终止条件
        return 1
    else:
        return n * factorial(n - 1)  # 线性递归

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)  # 非线性递归

在递归设计时，我们需要注意保持适当的终止条件，否则可能导致无限递归，从而引发栈溢出错误。

### 2.1.2 递归与迭代的比较

递归与迭代都是重复执行操作的方法，但二者在实现上有所不同。递归是通过函数自身调用实现重复，而迭代是通过循环语句来实现。在实际应用中，选择递归还是迭代，取决于问题本身的性质以及对性能的要求。

递归通常在代码结构上更加简洁明了，更适合表示自相似结构的问题，如树的遍历、汉诺塔问题等。然而，递归的缺点是可能会造成较大的内存消耗和性能损失，因为它需要为每次递归调用维护一个调用栈。

迭代则不需要额外的调用栈，因此在内存使用上相对更为高效，但其代码结构往往没有递归简洁。

### 2.1.3 性能优化策略

在实际开发中，递归函数往往伴随着大量的性能开销。为了提高性能，我们可以采取以下几种策略：

- 尾递归优化：尾递归是指递归调用是函数体中的最后一个动作，对于支持尾递归优化的编译器，可以将尾递归转换为迭代，从而节省调用栈空间。
- 记忆化：将已计算的递归结果存储起来，避免重复计算。这种技术称为记忆化（memoization），对于递归计算耗时的问题，能够显著提高效率。

示例代码：

# 使用记忆化优化斐波那契数列计算
fib_cache = {0: 0, 1: 1}

def fibonacci_memo(n):
    if n not in fib_cache:
        fib_cache[n] = fibonacci_memo(n - 1) + fibonacci_memo(n - 2)
    return fib_cache[n]

## 2.2 递归在数学中的应用

递归在数学中有广泛的应用，尤其在数列和几何学中，递归提供了一种描述自相似结构和复杂现象的数学工具。

### 2.2.1 数学序列与递归关系

递归关系是定义数列的一种方法，其中每一项都是前一项或前几项的函数。最著名的递归数列包括斐波那契数列、阶乘数列等。

递归数列通常可以通过递推公式进行描述，例如：

F(n) = F(n-1) + F(n-2) 其中 F(0) = 0, F(1) = 1

递归数列的计算和证明可以利用数学归纳法，这是一种利用递归思想来解决问题的方法。

### 2.2.2 递归在几何学中的体现

递归方法在几何学中的应用产生了分形几何学，分形几何学研究的是自相似结构在几何形态中的表现。

分形几何具有无限细分的特点，每一个局部都可以看作整体的缩小版，这种特性使得分形在描述自然现象时显示出强大的能力。

## 2.3 分形几何学的基础

### 2.3.1 分形的定义及其特征

分形是一种复杂且精细的几何形状，它具有一些特定的数学性质：自相似性、无限细分性和复杂的边界。分形结构可以是任意复杂的，且其复杂性在所有尺度上都存在。

### 2.3.2 分形理论的数学模型

分形理论涉及数学中的多个分支，包括拓扑学、测度论和动力系统理论等。著名的分形模型包括科赫雪花、曼德勃罗集合和谢尔宾斯基垫片等。

分形理论不仅在数学研究中有着重要地位，它在物理、生物、材料科学以及信息科学等领域也有广泛的应用。

在了解了递归理论的基础和数学原理后，我们对递归的定义、类型和在数学中的应用有了一个全面的认识。在此基础上，我们可以进一步探索递归与分形在自然界、艺术和科技中的应用，揭示其在现实世界中的广泛影响。

# 3. 自然界中的递归现象

自然界是递归和分形现象最直观的展示场所。从植物的生长模式到动物的体型特征，从地表的岩石结构到大气的气候模式，递归和分形的原理贯穿于自然界的各个角落。本章将深入探讨自然界中递归现象的具体体现，并分析其背后的科学原理。

## 3.1 生物学中的递归结构

在生物学中，递归现象普遍存在，它在植物和动物的生长与形态中表现出一种精妙的自我相似性。这种现象不仅揭示了生命的复杂性，也为科学研究提供了丰富的研究素材。

### 3.1.1 植物的递归生长模式

植物的生长往往遵循着递归的模式。例如，一棵树的分枝结构，从主干到小枝再到更小的枝叶，几乎呈现出一种有序的重复结构。这种模式在自然界中的普遍性使得植物学家对它进行了深入研究。

graph TD
    A[主干] -->|分支| B[主枝]
    B -->|分支| C[小枝]
    C -->|分支|