数组操作详解：遍历、查找、排序，掌握数组操作的必备技能

# 1. 数组的基本概念和操作

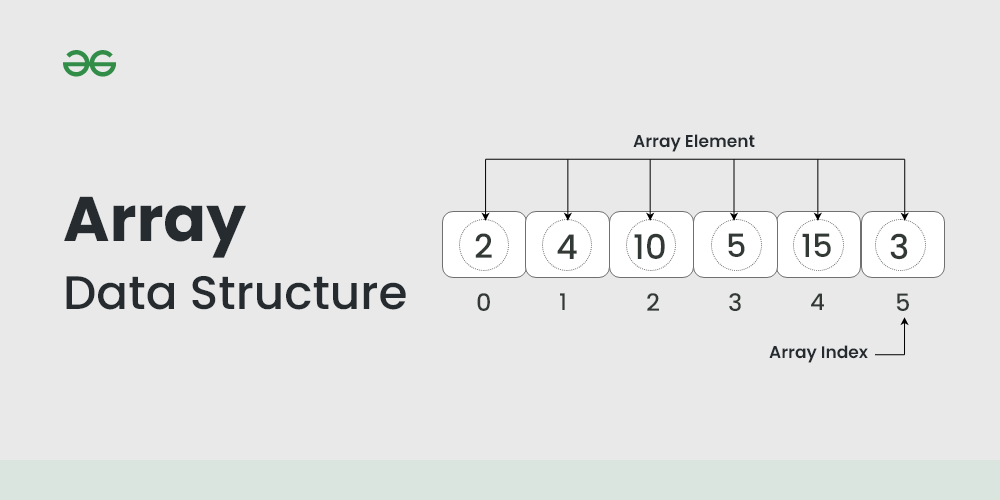
数组是一种数据结构，它存储一组具有相同数据类型的元素。每个元素都有一个索引，用于唯一标识它在数组中的位置。数组的长度是它包含的元素的数量。

数组的常见操作包括：

- **访问元素：**可以使用索引访问数组中的元素。例如，`array[i]` 表示数组中索引为 `i` 的元素。
- **插入元素：**可以在数组的末尾或指定索引处插入元素。
- **删除元素：**可以从数组中删除元素，并根据需要调整其他元素的索引。
- **遍历数组：**可以使用循环遍历数组中的所有元素。

# 2. 数组的遍历技巧

### 2.1 顺序遍历数组

顺序遍历数组是最简单、最常用的遍历方式，它从数组的第一个元素开始，依次访问每个元素，直到遍历到最后一个元素。

def sequential_traversal(arr):
    """顺序遍历数组

    Args:
        arr (list): 待遍历的数组

    Returns:
        None
    """
    for element in arr:
        print(element)

**逻辑分析：**

该代码使用 `for` 循环依次遍历数组中的每个元素，并打印每个元素。

**参数说明：**

* `arr`: 待遍历的数组，类型为列表。

### 2.2 逆序遍历数组

逆序遍历数组与顺序遍历相反，它从数组的最后一个元素开始，依次访问每个元素，直到遍历到第一个元素。

def reverse_traversal(arr):
    """逆序遍历数组

    Args:
        arr (list): 待遍历的数组

    Returns:
        None
    """
    for element in reversed(arr):
        print(element)

**逻辑分析：**

该代码使用 `reversed()` 函数将数组反转，然后使用 `for` 循环依次遍历反转后的数组中的每个元素，并打印每个元素。

**参数说明：**

* `arr`: 待遍历的数组，类型为列表。

### 2.3 跳跃遍历数组

跳跃遍历数组允许以指定的步长遍历数组，它从数组的第一个元素开始，以指定的步长访问每个元素，直到遍历到最后一个元素。

def jump_traversal(arr, step):
    """跳跃遍历数组

    Args:
        arr (list): 待遍历的数组
        step (int): 跳跃步长

    Returns:
        None
    """
    for i in range(0, len(arr), step):
        print(arr[i])

**逻辑分析：**

该代码使用 `range()` 函数生成一个步长为 `step` 的序列，然后使用 `for` 循环依次遍历该序列，并打印每个序列元素对应的数组元素。

**参数说明：**

* `arr`: 待遍历的数组，类型为列表。
* `step`: 跳跃步长，类型为整数。

### 2.4 嵌套遍历多维数组

多维数组是指具有多个维度的数组，例如二维数组、三维数组等。嵌套遍历多维数组需要使用嵌套循环，依次遍历每个维度的元素。

def nested_traversal(arr):
    """嵌套遍历多维数组

    Args:
        arr (list): 待遍历的多维数组

    Returns:
        None
    """
    for row in arr:
        for element in row:
            print(element)

**逻辑分析：**

该代码使用两个嵌套的 `for` 循环依次遍历多维数组中的每个元素，外层循环遍历每一行，内层循环遍历每一列。

**参数说明：**

* `arr`: 待遍历的多维数组，类型为列表。

# 3. 数组的查找算法

### 3.1 线性查找

线性查找是一种最简单的查找算法，其基本思想是顺序地遍历数组中的每个元素，并与给定的目标值进行比较。如果找到匹配的目标值，则返回其索引；否则，返回-1。

#### 3.1.1 顺序查找

顺序查找从数组的第一个元素开始，依次与目标值进行比较，直到找到匹配的元素或遍历完整个数组。其时间复杂度为 O(n)，其中 n 为数组的长度。

def sequential_search(arr, target):
    """
    顺序查找算法

    :param arr: 数组
    :param target: 目标值
    :return: 找到目标值的索引，否则返回 -1
    """
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

**逻辑分析：**

* 循环遍历数组中的每个元素。
* 比较每个元素与目标值。
* 如果找到匹配的元素，返回其索引。
* 如果遍历完整个数组仍未找到，返回 -1。

#### 3.1.2 二分查找

二分查找是一种更有效的查找算法，适用于已经排序的数组。其基本思想是将数组划分为两半，并根据目标值与中间元素进行比较。如果目标值小于中间元素，则在前半部分继续查找；如果目标值大于中间元素，则在后半部分继续查找。如此递归地缩小查找范围，直到找到目标值或确定目标值不在数组中。

def binary_search(arr, target):
    """
    二分查找算法

    :param arr: 排序好的数组
    :param target: 目标值
    :return: 找到目标值的索引，否则返回 -1
    """
    left, right = 0, len(arr) - 1

    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1

    return -1

**逻辑分析：**

* 初始化左右指针指向数组的开头和结尾。
* 循环缩小查找范围，直到找到目标值或确定目标值不在数组中。
* 计算中间索引并与目标值进行比较。
* 根据比较结果调整左右指针。
* 时间复杂度为 O(log n)，其中 n 为数组的长度。

### 3.2 哈希查找

哈希查找是一种基于哈希函数的查找算法。其基本思想是将每个元素映射到一个哈希值，然后使用哈希值快速定位元素。哈希函数是一个将输入值转换为哈希值（通常是整数）的函数。

#### 3.2.1 哈希函数的设计

哈希函数的设计至关重要，因为它影响查找的效率和哈希冲突的可能性。一个好的哈希函数应该具有以下特性：

* **均匀分布：**将输入值均匀地映射到哈希值空间。
* **快速计算：**可以在短时间内计算哈希值。
* **确定性：**对于相同的输入值，始终返回相同的哈希值。

常用的哈希函数包括：

* **模运算：**将输入值对一个常数取模，得到哈希值。
* **位运算：**对输入值的二进制位进行位操作，得到哈希值。
* **乘法哈希：**将输入值与一个常数相乘，取结果的低位作为哈希值。

#### 3.2.2 哈希冲突的解决

哈希冲突是指不同的输入值映射到相同的哈希值。为了解决哈希冲突，可以使用以下方法：

* **链地址法：**将具有相同哈希值的元素存储在链表中。
* **开放寻址法：**在哈希表中找到一个空槽来存储具有相同哈希值的元素。
* **再哈希：**使用另一个哈希函数重新计算具有相同哈希值的元素的哈希值。

# 4. 数组的排序算法

在数据处理中，排序是至关重要的操作，它可以将数据按特定顺序排列，方便后续的处理和分析。数组作为一种重要的数据结构，提供了高效的排序算法，本章节将深入探讨数组的排序算法，包括冒泡排序、选择排序和插入排序。

### 4.1 冒泡排序

冒泡排序是一种简单直观的排序算法，它通过反复比较相邻元素，将较大的元素“冒泡”到数组末尾。

#### 4.1.1 基本冒泡排序

def bubble_sort(arr):
    for i in range(len(arr) - 1):
        for j in range(len(arr) - 1 - i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

**代码逻辑分析：**

* 外层循环 `for i in range(len(arr) - 1)` 遍历数组，控制冒泡的次数。
* 内层循环 `for j in range(len(arr) - 1 - i)` 在未排序的部分中进行比较。
* 如果 `arr[j]` 大于 `arr[j + 1]`，则交换两个元素。

#### 4.1.2 优化冒泡排序

基本冒泡排序存在时间复杂度高的缺点，可以通过以下优化措施提高效率：

* **提前退出：**如果内层循环没有进行任何交换，说明数组已经有序，可以提前退出。

def optimized_bubble_sort(arr):
    for i in range(len(arr) - 1):
        swapped = False  # 记录是否进行交换
        for j in range(len(arr) - 1 - i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                swapped = True
        if not swapped:  # 如果没有交换，说明已经有序
            break

### 4.2 选择排序

选择排序是一种基于选择思想的排序算法，它通过反复选择数组中最小的元素，将其与当前位置的元素交换。

#### 4.2.1 基本选择排序

def selection_sort(arr):
    for i in range(len(arr) - 1):
        min_index = i  # 记录最小元素的索引
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[min_index]:
                min_index = j
        arr[i], arr[min_index] = arr[min_index], arr[i]

**代码逻辑分析：**

* 外层循环 `for i in range(len(arr) - 1)` 遍历数组，控制排序的次数。
* 内层循环 `for j in range(i + 1, len(arr))` 在未排序的部分中查找最小元素。
* 如果 `arr[j]` 小于 `arr[min_index]`，则更新最小元素的索引 `min_index`。
* 最后，将最小元素与当前位置的元素交换。

#### 4.2.2 堆排序

堆排序是一种基于堆数据结构的排序算法，它通过构建一个最大堆，然后依次弹出堆顶元素，即可得到一个有序数组。

def heap_sort(arr):
    # 构建最大堆
    for i in range(len(arr) // 2 - 1, -1, -1):
        heapify(arr, i, len(arr))

    # 依次弹出堆顶元素
    for i in range(len(arr) - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        heapify(arr, 0, i)

def heapify(arr, i, n):
    largest = i  # 记录最大元素的索引
    left = 2 * i + 1  # 左子节点索引
    right = 2 * i + 2  # 右子节点索引

    if left < n and arr[left] > arr[largest]:
        largest = left

    if right < n and arr[right] > arr[largest]:
        largest = right

    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, largest, n)

**代码逻辑分析：**

* `heapify` 函数构建一个以 `i` 为根节点的最大堆。
* `heap_sort` 函数依次弹出堆顶元素，并重建堆。
* 通过这种方式，数组中的元素逐渐按降序排列，最后得到一个有序数组。

### 4.3 插入排序

插入排序是一种基于插入思想的排序算法，它通过将元素逐个插入到已排序的部分，从而得到一个有序数组。

#### 4.3.1 基本插入排序

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key

**代码逻辑分析：**

* 外层循环 `for i in range(1, len(arr))` 遍历数组，控制插入的次数。
* 内层循环 `while j >= 0 and key < arr[j]` 找到插入位置。
* 将已排序部分的元素向后移动，为 `key` 腾出空间。
* 最后，将 `key` 插入到合适的位置。

#### 4.3.2 希尔排序

希尔排序是一种基于插入排序的改进算法，它通过分段插入的方式，提高了排序效率。

def shell_sort(arr):
    gap = len(arr) // 2
    while gap > 0:
        for i in range(gap, len(arr)):
            key = arr[i]
            j = i - gap
            while j >= 0 and key < arr[j]:
                arr[j + gap] = arr[j]
                j -= gap
            arr[j + gap] = key
        gap //= 2

**代码逻辑分析：**

* `gap` 变量控制分段插入的间隔。
* 外层循环 `for i in range(gap, len(arr))` 遍历数组，控制插入的次数。
* 内层循环 `while j >= 0 and key < arr[j]` 找到插入位置。
* 将已排序部分的元素向后移动，为 `key` 腾出空间。
* 最后，将 `key` 插入到合适的位置。
* `gap` 逐渐减小，直到为 1，此时算法退化为基本插入排序。

# 5. 数组的应用实践

### 5.1 数组在数据统计中的应用

数组在数据统计中有着广泛的应用，可以用来统计各种类型的数据，例如：

# 统计不同年龄段的人数
age_groups = [0, 10, 20, 30, 40, 50, 60, 70, 80, 90]
age_counts = [0] * len(age_groups)

for age in ages:
    for i in range(len(age_groups)):
        if age >= age_groups[i] and age < age_groups[i+1]:
            age_counts[i] += 1

### 5.2 数组在字符串处理中的应用

数组在字符串处理中也扮演着重要的角色，可以用来存储和操作字符串：

# 统计字符串中每个字符出现的次数
characters = list("Hello world")
character_counts = [0] * 26

for character in characters:
    character_index = ord(character) - ord('a')
    character_counts[character_index] += 1

### 5.3 数组在图像处理中的应用

数组在图像处理中有着至关重要的作用，可以用来表示和处理图像数据：

# 创建一个二维数组来表示图像
image = [[0, 0, 0],
         [0, 255, 0],
         [0, 0, 0]]

# 将图像灰度化
for row in range(len(image)):
    for col in range(len(image[row])):
        image[row][col] = (image[row][col][0] + image[row][col][1] + image[row][col][2]) // 3