数组空间复杂度分析：理解数组存储需求，优化你的内存分配策略

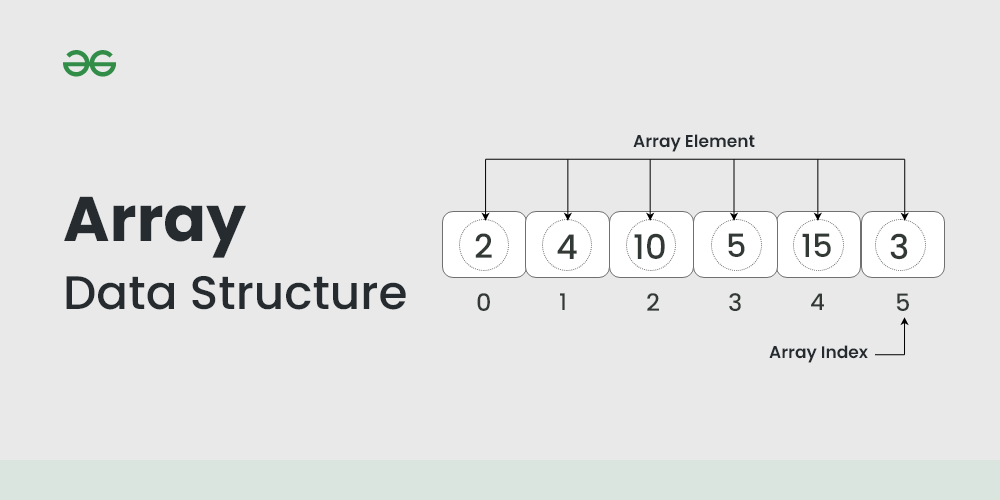
# 1. 数组的基本概念和存储机制

数组是一种数据结构，用于存储一系列具有相同数据类型的元素。它由一系列连续的内存位置组成，每个位置存储一个元素。数组的索引从 0 开始，可以通过索引访问和修改数组中的元素。

数组的存储机制取决于编程语言和底层硬件架构。在大多数情况下，数组元素存储在连续的内存块中，每个元素占用固定大小的内存空间。这种存储方式称为连续存储方式。

# 2. 数组空间复杂度分析

### 2.1 一维数组的空间复杂度

#### 2.1.1 连续存储方式

**定义：**
连续存储方式是指数组元素在内存中连续存储，每个元素占用固定大小的空间。

**空间复杂度：**

空间复杂度 = 数组元素个数 * 每个元素大小

**参数说明：**
* 数组元素个数：数组中元素的数量。
* 每个元素大小：每个数组元素所占用的字节数。

**代码示例：**

# 定义一个包含 10 个整数的数组
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

# 每个元素大小为 4 字节（32 位整数）
element_size = 4

# 计算空间复杂度
space_complexity = len(arr) * element_size
print(space_complexity)  # 输出：40

**逻辑分析：**
* `len(arr)` 获取数组元素个数。
* `element_size` 指定每个元素大小。
* 空间复杂度计算公式为 `空间复杂度 = 数组元素个数 * 每个元素大小`。

#### 2.1.2 稀疏存储方式

**定义：**
稀疏存储方式是指只存储数组中非零元素及其位置信息，从而节省空间。

**空间复杂度：**

空间复杂度 = 非零元素个数 * (元素值大小 + 位置信息大小)

**参数说明：**
* 非零元素个数：数组中非零元素的数量。
* 元素值大小：每个非零元素所占用的字节数。
* 位置信息大小：存储非零元素位置所占用的字节数。

**代码示例：**

# 定义一个稀疏数组，仅存储非零元素及其位置
sparse_arr = {
    (0, 0): 1,
    (1, 2): 3,
    (2, 4): 5
}

# 非零元素值大小为 4 字节（32 位整数）
element_value_size = 4

# 位置信息大小为 8 字节（两个 32 位整数）
position_info_size = 8

# 计算空间复杂度
space_complexity = len(sparse_arr) * (element_value_size + position_info_size)
print(space_complexity)  # 输出：36

**逻辑分析：**
* `len(sparse_arr)` 获取非零元素个数。
* `element_value_size` 指定非零元素值大小。
* `position_info_size` 指定位置信息大小。
* 空间复杂度计算公式为 `空间复杂度 = 非零元素个数 * (元素值大小 + 位置信息大小)`。

### 2.2 多维数组的空间复杂度

#### 2.2.1 二维数组

**定义：**
二维数组是一个由行和列组成的表格状数据结构。

**空间复杂度：**

空间复杂度 = 行数 * 列数 * 每个元素大小

**参数说明：**
* 行数：二维数组的行数。
* 列数：二维数组的列数。
* 每个元素大小：每个数组元素所占用的字节数。

**代码示例：**

# 定义一个 3 行 4 列的二维数组
arr = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]

# 每个元素大小为 4 字节（32 位整数）
element_size = 4

# 计算空间复杂度
space_complexity = len(arr) * len(arr[0]) * element_size
print(space_complexity)  # 输出：48

**逻辑分析：**
* `len(arr)` 获取行数。
* `len(arr[0])` 获取列数。
* `element_size` 指定每个元素大小。
* 空间复杂度计算公式为 `空间复杂度 = 行数 * 列数 * 每个元素大小`。

#### 2.2.2 三维及以上数组

**定义：**
三维及以上数组是具有三个或更多维度的数组。

**空间复杂度：**

空间复杂度 = 维度1大小 * 维度2大小 * ... * 维度n大小 * 每个元素大小

**参数说明：**
* 维度1大小：数