数组在算法中的应用：查找、排序、动态规划，解锁算法的强大力量

# 1. 数组的基本概念和操作**

数组是一种数据结构，它存储相同类型元素的集合，每个元素都有一个唯一的索引。数组可以通过索引访问，并且可以对数组进行各种操作，如插入、删除和排序。

数组的声明和初始化可以使用以下语法：

int[] arr = new int[5]; // 声明一个长度为5的整型数组

数组元素可以通过索引访问，索引从0开始。例如，要访问第一个元素，可以使用以下语法：

int firstElement = arr[0];

# 2. 数组在查找算法中的应用

数组在查找算法中扮演着至关重要的角色，提供了一种高效的方式来搜索和定位特定元素。本章将深入探讨两种基本的查找算法：线性查找和二分查找，并分析它们的原理、时间复杂度、优化策略和应用场景。

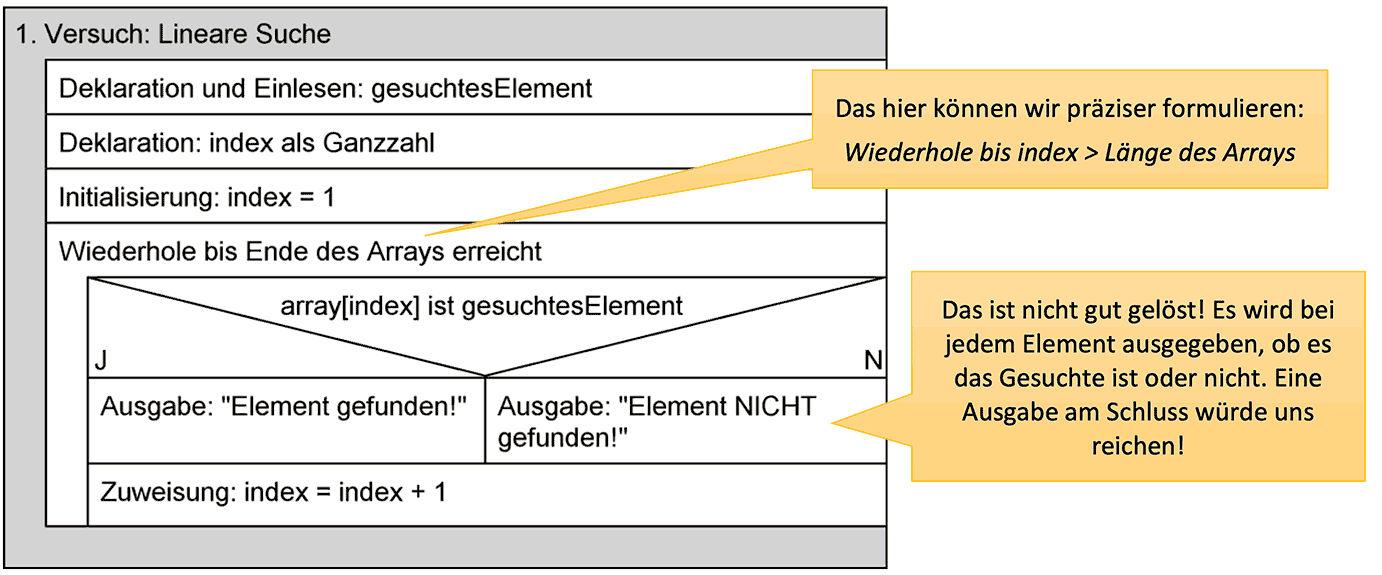
### 2.1 线性查找

#### 2.1.1 算法原理和时间复杂度

线性查找，也称为顺序查找，是一种最简单的查找算法。它从数组的第一个元素开始，依次检查每个元素，直到找到目标元素或遍历完整个数组。

def linear_search(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

线性查找的时间复杂度为 O(n)，其中 n 是数组的长度。这是因为在最坏的情况下，算法需要遍历整个数组才能找到目标元素。

#### 2.1.2 优化策略和应用场景

虽然线性查找的时间复杂度较高，但在某些情况下它仍然是一种有用的算法：

- **数组较小：**当数组较小（例如，小于 100 个元素）时，线性查找的开销可以忽略不计。
- **目标元素分布均匀：**如果目标元素在数组中分布均匀，线性查找可以快速找到它，因为平均情况下只需要遍历数组的一半。
- **查找第一个匹配项：**线性查找可以快速找到数组中第一个匹配目标元素的项。

### 2.2 二分查找

#### 2.2.1 算法原理和时间复杂度

二分查找是一种高效的查找算法，它利用数组的有序特性来缩小搜索范围。算法通过将数组划分为两半，并根据目标元素与中间元素的关系来确定目标元素位于哪一半，以此不断缩小搜索范围。

def binary_search(arr, target):
    low = 0
    high = len(arr) - 1

    while low <= high:
        mid = (low + high) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            low = mid + 1
        else:
            high = mid - 1

    return -1

二分查找的时间复杂度为 O(log n)，其中 n 是数组的长度。这是因为算法每次将搜索范围缩小一半，因此最多需要 log n 次迭代即可找到目标元素。

#### 2.2.2 适用条件和实现方法

二分查找适用于以下条件：

- **数组已排序：**二分查找要求数组必须按升序或降序排序。
- **目标元素唯一：**如果数组中有多个与目标元素相等的元素，二分查找只能找到第一个匹配项。

二分查找可以采用递归或迭代的方式实现。递归实现如下：

def binary_search_recursive(arr, target, low, high):
    if low > high:
        return -1

    mid = (low + high) // 2
    if arr[mid] == target:
        return mid
    elif arr[mid] < target:
        return binary_search_recursive(arr, target, mid + 1, high)
    else:
        return binary_search_recursive(arr, target, low, mid - 1)

# 3. 数组在排序算法中的应用

### 3.1 冒泡排序

#### 3.1.1 算法原理和时间复杂度

冒泡排序是一种简单直观的排序算法，其基本思想是：逐个比较相邻元素，如果前一个元素大于后一个元素，则交换它们的位置。重复这一过程，直到所有元素按升序排列。

def bubble_sort(arr):
    """冒泡排序算法"""
    n = len(arr)
    for i in range(n):
        for j in range(n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

**时间复杂度：**

冒泡排序的时间复杂度为 O(n^2)，其中 n 为数组的长度。这是因为算法需要遍历数组 n 次，每次遍历都需要比较 n-1 对元素。

#### 3.1.2 优化策略和应用场景

**优化策略：**

* **标记已排序元素：**在每次比较后，如果元素已经按顺序排列，则可以标记它们为已排序，这样可以减少后续比较的次数。
* **优化内循环：**在内循环中，可以只比较未标记为已排序的元素，进一步减少比较次数。

**应用场景：**

冒泡排序适用于小规模数组的排序，或者数据已经基本有序的情况下。由于其简单易懂，在教学和演示中经常被用作排序算法的入门示例。

### 3.2 选择排序

#### 3.2.1 算法原理和时间复杂度

选择排序是一种基于选择思想的排序算法。其基本思想是：每次从剩余未排序的元素中选择最小的元素，将其与当前最小元素交换位置。重复这一过程，直到所有元素按升序排列。

def selection_sort(arr):
    """选择排序算法"""
    n = len(arr)
    for i in range(n):
        min_idx = i
        for j in range(i + 1, n):