分布式系统中的数据压缩算法：提升数据传输效率，优化集群性能

# 1. 分布式系统中的数据压缩概述**

数据压缩是减少数据大小的过程，在分布式系统中，数据压缩具有重要意义。通过压缩数据，可以优化数据传输，节省存储空间，并提高集群性能。

数据压缩算法可分为无损压缩和有损压缩。无损压缩算法不丢失任何数据，而有损压缩算法则会牺牲一些数据精度以实现更高的压缩率。在分布式系统中，根据不同的应用场景和数据类型，需要选择合适的压缩算法。

# 2. 数据压缩算法的理论基础

### 2.1 无损压缩算法

无损压缩算法可以将数据压缩到尽可能小的尺寸，同时不丢失任何信息。这意味着解压缩后的数据与原始数据完全相同。无损压缩算法通常用于需要精确性的数据，例如文本文件、图像和音频文件。

#### 2.1.1 霍夫曼编码

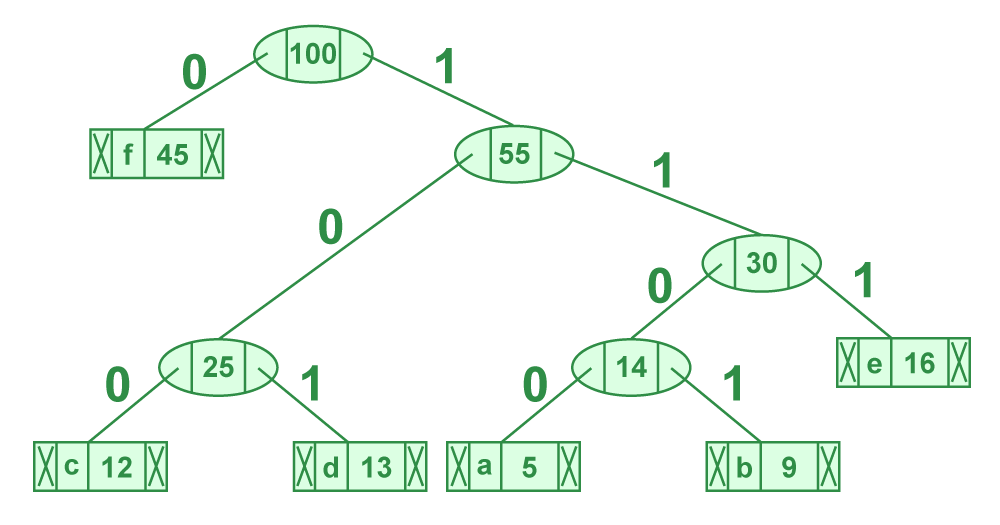
霍夫曼编码是一种无损压缩算法，它通过为每个符号分配一个可变长度的代码来工作。代码的长度与符号出现的频率成反比，因此出现的频率较高的符号使用较短的代码。霍夫曼编码的优点是它可以实现非常高的压缩率，同时保持无损压缩。

def huffman_encode(data):
    """
    霍夫曼编码算法

    参数：
        data: 要编码的数据

    返回：
        编码后的数据
    """

    # 计算每个符号的频率
    freq = {}
    for symbol in data:
        if symbol not in freq:
            freq[symbol] = 0
        freq[symbol] += 1

    # 创建霍夫曼树
    tree = create_huffman_tree(freq)

    # 为每个符号分配霍夫曼代码
    codes = {}
    assign_codes(tree, "", codes)

    # 编码数据
    encoded_data = ""
    for symbol in data:
        encoded_data += codes[symbol]

    return encoded_data

def create_huffman_tree(freq):
    """
    创建霍夫曼树

    参数：
        freq: 符号频率字典

    返回：
        霍夫曼树
    """

    # 创建叶子节点
    nodes = []
    for symbol, frequency in freq.items():
        nodes.append(Node(symbol, frequency))

    # 构建霍夫曼树
    while len(nodes) > 1:
        # 找到频率最低的两个节点
        n1 = min(nodes, key=lambda x: x.frequency)
        nodes.remove(n1)
        n2 = min(nodes, key=lambda x: x.frequency)
        nodes.remove(n2)

        # 创建父节点
        parent = Node(None, n1.frequency + n2.frequency)
        parent.left = n1
        parent.right = n2

        # 将父节点添加到节点列表中
        nodes.append(parent)

    return nodes[0]

def assign_codes(node, code, codes):
    """
    为每个符号分配霍夫曼代码

    参数：
        node: 当前节点
        code: 当前代码
        codes: 符号代码字典
    """

    if node.symbol is not None:
        codes[node.symbol] = code
    else:
        assign_codes(node.left, code + "0", codes)
        assign_codes(node.right, code + "1", codes)

#### 2.1.2 Lempel-Ziv-Welch (LZW) 算法

LZW算法是一种无损压缩算法，它通过将重复的子字符串替换为较短的代码来工作。LZW算法的优点是它可以实现非常高的压缩率，并且它适用于各种类型的数据。

def lzw_encode(data):
    """
    LZW编码算法

    参数：
        data: 要编码的数据

    返回：
        编码后的数据
    """

    # 创建字典
    dictionary = {}
    for i in range(256):
        dictionary[chr(i)] = i

    # 初始化编码结果
    encoded_data = []

    # 扫描数据
    w = ""
    for c in data:
        wc = w + c
        if wc in dictionary:
            w = wc
        else:
            encoded_data.append(dictionary[w])
            dictionary[wc] = len(dictionary)
            w = c

    # 添加最后一个编码
    encoded_data.append(dictionary[w])

    return encoded_data

def lzw_decode(encoded_data):
    """
    LZW解码算法

    参数：
        encoded_data: 要解码的数据

    返回：
        解码后的数据
    """

    # 创建字典
    dictionary = {}
    for i in range(256):
        dictionary[i] = chr(i)

    # 初始化解码结果