数据压缩算法的优化：提升压缩效率，降低资源消耗

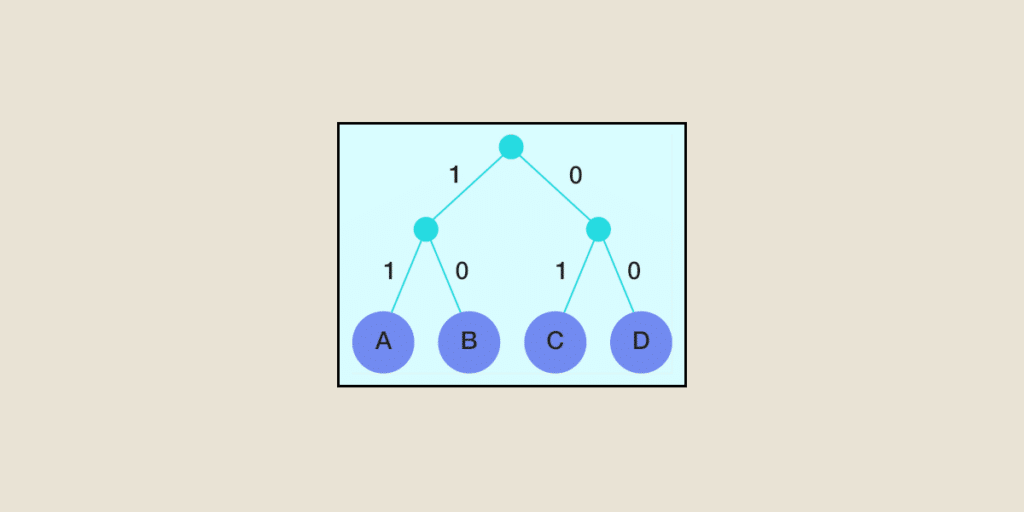
# 1. 数据压缩算法概述

数据压缩算法是一种技术，用于减少数据的大小，同时保持其完整性或以可接受的方式降低失真度。它在各种领域有着广泛的应用，包括文件压缩、图像压缩和视频压缩。

数据压缩算法通常分为两类：无损压缩和有损压缩。无损压缩算法可以完美地还原原始数据，而有损压缩算法则会引入一些失真，以实现更高的压缩率。在选择压缩算法时，需要考虑压缩率和失真度之间的权衡。

# 2 数据压缩算法的理论基础

### 2.1 数据压缩的原理和分类

数据压缩是一种将数据表示为更紧凑形式的技术，从而减少其存储或传输所需的空间。其基本原理是利用数据的冗余性，即数据中存在着重复或可预测的模式。通过识别和消除这些冗余，可以显著减少数据的大小。

数据压缩算法可分为两大类：

- **无损压缩：**在压缩和解压缩过程中不损失任何数据，恢复的原始数据与原始数据完全相同。
- **有损压缩：**允许一定程度的数据丢失，以实现更高的压缩率。在某些情况下，丢失的数据对应用程序来说是不可感知的。

### 2.2 无损压缩与有损压缩

**无损压缩**算法通常使用编码技术，例如霍夫曼编码或算术编码，将数据表示为更紧凑的二进制表示。这些算法通过分配较短的代码给出现频率较高的符号，从而减少了数据的长度。

**有损压缩**算法利用数据中的冗余性，通过丢弃或近似某些数据来实现更高的压缩率。例如，JPEG图像压缩算法使用离散余弦变换 (DCT) 将图像分解为频率分量，然后丢弃高频分量，因为人眼对这些分量不太敏感。

### 2.3 压缩率与失真度之间的权衡

压缩率是指压缩后的数据大小与原始数据大小之比。更高的压缩率意味着更小的文件大小，但可能以牺牲数据质量为代价。

失真度是指压缩后数据与原始数据之间的差异。对于无损压缩，失真度为 0，而对于有损压缩，失真度会随着压缩率的增加而增加。

在选择压缩算法时，需要考虑压缩率和失真度之间的权衡。对于需要保持数据完整性的应用程序，应使用无损压缩算法。对于允许一定程度数据丢失的应用程序，有损压缩算法可以提供更高的压缩率。

**代码块：**

def compress(data, algorithm):
    """
    根据指定的算法压缩数据。

    参数：
        data: 要压缩的数据
        algorithm: 压缩算法，例如 "huffman" 或 "jpeg"
    """
    if algorithm == "huffman":
        return huffman_encode(data)
    elif algorithm == "jpeg":
        return jpeg_encode(data)
    else:
        raise ValueError("不支持的压缩算法：" + algorithm)

**逻辑分析：**

该代码定义了一个 `compress` 函数，用于根据指定的算法压缩数据。函数接受两个参数：要压缩的数据和压缩算法。函数根据算法类型调用相应的编码函数，例如 `huffman_encode` 或 `jpeg_encode`。如果指定的算法不受支持，函数将引发一个 `ValueError` 异常。

**参数说明：**

- `data`：要压缩的数据。
- `algorithm`：压缩算法，例如 "huffman" 或 "jpeg"。

# 3.1 常用的数据压缩算法

#### 3.1.1 Huffman编码

Huffman编码是一种无损压缩算法，它通过为每个符号分配可变长度的代码来实现压缩。符号出现的频率越高，分配的代码就越短。Huffman编码算法的步骤如下：

1. 计算每个符号出现的频率。
2. 创建一个优先级队列，其中符号按频率从小到大排序。
3. 重复以下步骤，直到队列中只有一个元素：
- 从队列中取出频率最低的两个符号。
- 创建一个新的符号，其频率等于两个符号频率之和。
- 将新符号插入队列中，并为其分配一个代码，该代码是两个符号代码的连接。
4. 为每个符号分配一个代码，该代码是从根节点到该符号节点的路径上的代码的连接。

**代码块：**

def huffman_encoding(data):
    """
    Huffman编码算法

    参数：
        data: 输入数据

    返回：
        编码后的数据
    """

    # 计算符号频率
    freq = {}
    for symbol in data:
        if symbol not in freq:
            freq[symbol] = 0
        freq[symbol] += 1

    # 创建优先级队列
    pq = PriorityQueue()
    for symbol, freq in freq.items():
        pq.put((freq, symbol))

    # 构建哈夫曼树
    while pq.size() > 1:
        freq1, symbol1 = pq.get()
        freq2, symbol2 = pq.get()
        new_freq = freq1 + freq2
        new_s