数据压缩算法的性能分析：揭秘压缩效率和速度的奥秘

# 1. 数据压缩算法概述

数据压缩算法是一种用于减少数据大小的技术，同时保持或恢复原始数据的完整性。它在各种应用中至关重要，包括文件存储、网络传输和多媒体处理。

数据压缩算法通常分为两类：无损压缩和有损压缩。无损压缩算法可以完美地重建原始数据，而有损压缩算法则允许一定程度的数据丢失，以实现更高的压缩比。

在选择数据压缩算法时，需要考虑以下因素：压缩效率、压缩速度、算法复杂度和实现成本。

# 2. 数据压缩算法的理论基础

数据压缩算法的理论基础主要分为无损压缩和有损压缩两大类。

### 2.1 无损压缩算法

无损压缩算法能够在不丢失任何原始数据的情况下对数据进行压缩。常用的无损压缩算法包括哈夫曼编码和算术编码。

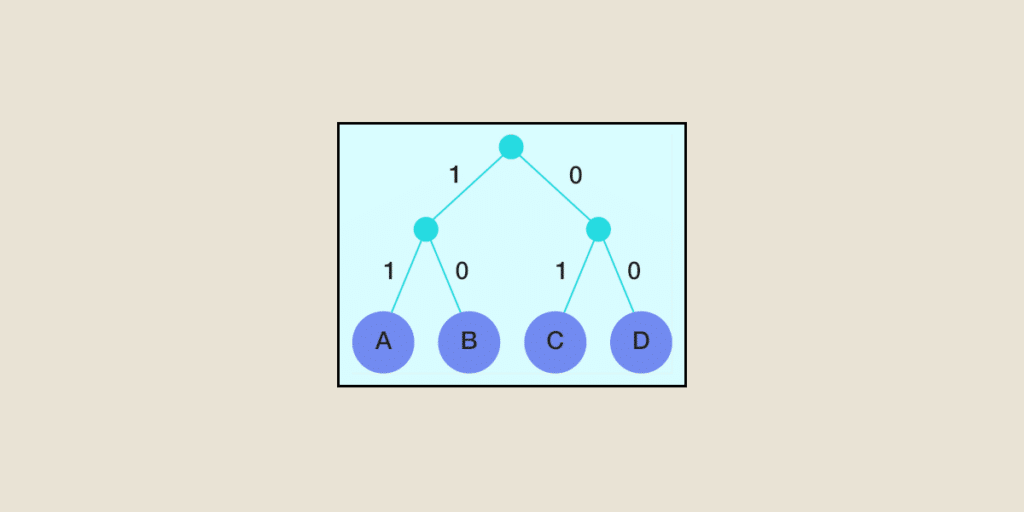
#### 2.1.1 哈夫曼编码

哈夫曼编码是一种基于统计学原理的无损压缩算法。其核心思想是：出现频率高的符号分配较短的编码，出现频率低的符号分配较长的编码。

**哈夫曼编码算法流程：**

1. 计算每个符号出现的频率。
2. 创建一个优先级队列，其中符号按频率递增排序。
3. 从队列中取出频率最低的两个符号。
4. 创建一个新的符号，其频率为这两个符号频率之和。
5. 将新符号插入队列中。
6. 重复步骤 3-5，直到队列中只剩下一个符号。
7. 为每个符号分配编码，编码长度为从根节点到该符号节点的路径长度。

**代码块：**

import heapq

def huffman_encoding(symbols, frequencies):
    """
    哈夫曼编码算法

    参数：
        symbols：符号列表
        frequencies：符号频率列表

    返回：
        符号编码字典
    """

    # 创建符号-频率字典
    symbol_freq_dict = dict(zip(symbols, frequencies))

    # 创建优先级队列
    queue = []
    for symbol, freq in symbol_freq_dict.items():
        heapq.heappush(queue, (freq, symbol))

    # 构建哈夫曼树
    while len(queue) > 1:
        freq1, symbol1 = heapq.heappop(queue)
        freq2, symbol2 = heapq.heappop(queue)

        new_freq = freq1 + freq2
        new_symbol = symbol1 + symbol2

        heapq.heappush(queue, (new_freq, new_symbol))

    # 为符号分配编码
    encoding_dict = {}
    code = ""
    while queue:
        freq, symbol = heapq.heappop(queue)
        encoding_dict[symbol] = code
        code += "0" if symbol == symbol1 else "1"
        code = code[:-1]

    return encoding_dict

**逻辑分析：**

* `huffman_encoding` 函数接受符号列表和频率列表作为参数，返回符号编码字典。
* 函数首先创建一个符号-频率字典，然后创建一个优先级队列，其中符号按频率递增排序。
* 接下来，函数构建哈夫曼树，直到队列中只剩下一个符号。
* 最后，函数为符号分配编码，编码长度为从根节点到该符号节点的路径长度。

#### 2.1.2 算术编码

算术编码也是一种无损压缩算法，它将输入数据表示为一个分数，然后使用算术运算对分数进行编码。

**算术编码算法流程：**

1. 将输入数据转换为符号序列。
2. 计算每个符号的概率。
3. 构建一个累积概率分布表。
4. 将输入数据转换为一个分数，分数范围为 [0, 1]。
5. 将分数分解为整数部分和小数部分。
6. 使用整数部分作为编码的索引，使用小数部分作为编码的权重。
7. 重复步骤 5-6，直到分数为 0。

**代码块：**

import math

def arithmetic_encoding(symbols, probabilities):
    """
    算术编码算法

    参数：
        symbols：符号列表
        probabilities：符号概率列表

    返回：
        编码后的比特流
    """

    # 计算累积概率分布表
    cumulative_probabilities = [0]
    for probability in probabilities:
        cumulative_probabilities.append(cumulative_probabilities[-1] + probability)

    # 转换为分数
    fraction = 0
    for symbol, probability in zip(symbols, probabilities):
        fraction += probability * (1 / cumul