【多元统计分析】：R语言高级数据分析必学方法

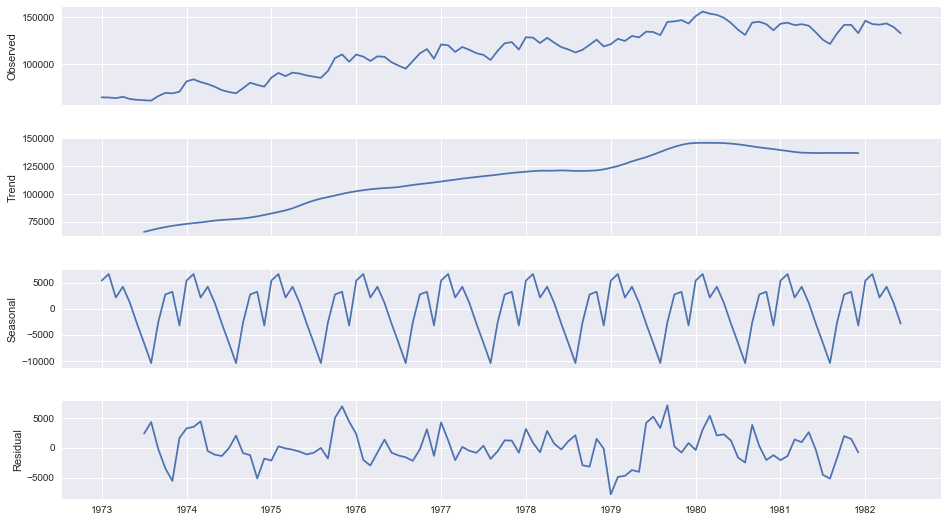
# 1. 多元统计分析概述

## 多元统计分析的定义
多元统计分析是一种应用数学方法，用于处理两个或两个以上变量的统计问题。它可以帮助研究者探索数据结构、发现变量之间的关系，以及对数据进行分类和预测。

## 分析方法的多样性
多元统计分析领域包括了一系列技术，如主成分分析（PCA）、聚类分析、判别分析、因子分析、回归分析和时间序列分析等。这些技术各有其应用场景，但共同的目的都是为了从复杂的数据集中提取有价值的信息。

## 应用场景
在不同的研究和行业领域，多元统计分析都有广泛的应用。例如，在生物信息学中，它可以帮助解释基因表达数据；在商业分析中，它可以用于市场细分和客户行为分析；在社会科学领域，它用于探索影响人口统计学的因素。

多元统计分析作为一种强大的数据分析工具，能够为我们提供深入的洞察力，帮助我们更好地理解复杂的数据集。在接下来的章节中，我们将深入探讨如何利用R语言来实现这些统计分析。

# 2. R语言基础与数据处理

## 2.1 R语言简介
### 2.1.1 R语言的特点与发展历程
R语言是一种用于统计计算和图形表示的编程语言和软件环境。其名称来源于字母“R”，是Robert Gentleman和Ross Ihaka两位创建者名字的首字母。R语言的开发始于1992年，并且从1997年起在GNU通用公共许可证下作为自由软件发布。R语言的特性和发展历程可归纳如下：

- **强大的统计分析能力**：R语言拥有众多的统计分析包，广泛应用于各种数据分析领域，如金融、生物信息、医药统计等。
- **开放性与社区支持**：R语言的开源特性使其拥有庞大的开发者和用户社区，为R语言贡献了大量扩展包。
- **图形表现力强**：R语言的图形系统极其强大，提供了高质量的图形输出，方便数据可视化。
- **跨平台兼容性**：R语言可在各种操作系统上运行，包括Windows、MacOS和Linux。
- **编程语言特性**：R语言支持完整的编程特性，包括函数编写、控制语句、循环、对象系统等。
- **集成其他语言**：R语言可以和其他编程语言，如C、C++、Java等进行集成，扩展其性能和功能。
### 2.1.2 R语言的安装与配置

安装R语言通常比较简单，可按照以下步骤进行：

1. 访问R语言官方网站（***）下载对应的安装程序。
2. 根据操作系统选择安装包进行下载。
3. 运行安装包，接受许可协议，并根据向导进行安装。
4. 安装完成后，在命令行输入`R`命令，如果成功启动R控制台，则表示安装成功。

配置R语言环境包括安装R包和设置工作路径等操作。具体步骤如下：

1. 打开R控制台，输入`install.packages("package_name")`来安装所需的R包。
2. 使用`setwd("path")`设置R的工作路径。
3. 配置CRAN镜像站点，通过`chooseCRANmirror()`选择最近的镜像站点以提高下载速度。

配置环境变量确保R可以在命令行中使用。在Windows系统中，通常需要将R的安装路径添加到环境变量`PATH`中。

## 2.2 R语言数据类型与结构

### 2.2.1 向量、矩阵和数组

向量是R语言中最基础的数据结构，可以包含多个相同类型的元素。以下是创建向量和操作向量的代码示例：

# 创建一个数值向量
numeric_vector <- c(1, 2, 3, 4)

# 创建一个字符向量
character_vector <- c("apple", "banana", "cherry")

# 访问向量中的第三个元素
third_element <- numeric_vector[3]

矩阵是二维的数值结构，具有固定数量的行和列。而数组可以看作是多维的矩阵。以下是如何创建矩阵和数组的示例：

# 创建一个3x3的矩阵
matrix <- matrix(c(1:9), nrow=3, ncol=3)

# 创建一个3x3x3的三维数组
array <- array(1:27, dim=c(3,3,3))

### 2.2.2 数据框与列表

数据框（Data Frame）是一种以行和列组织的数据结构，列可以包含不同的数据类型。列表（List）则可以包含不同类型和结构的数据元素。以下是数据框和列表的创建示例：

# 创建一个数据框
data_frame <- data.frame(
  name=c("John", "Anna", "Peter"),
  age=c(28, 34, 29),
  gender=c("M", "F", "M")
)

# 创建一个列表
list_example <- list(
  vector = c(1, 2, 3),
  matrix = matrix(1:6, nrow=2),
  dataframe = data_frame
)

## 2.3 R语言数据输入输出

### 2.3.1 从文件读取数据

R语言提供了多种函数用于从不同格式的文件中读取数据，常见的有`read.csv()`, `read.table()`, `read.xlsx()`等。以下是读取CSV文件的示例：

# 读取CSV文件
data <- read.csv("path_to_file.csv")

### 2.3.2 数据的导出与保存

数据处理完成后，可能需要将其导出或保存到文件中，R语言中常用的函数包括`write.csv()`, `write.table()`, `write.xlsx()`等。以下是如何将数据框保存为CSV文件的示例：

# 将数据框导出为CSV文件
write.csv(data, file="path_to_output_file.csv", row.names=FALSE)

以上章节内容覆盖了R语言的基础知识，从软件安装配置，数据结构介绍，到数据的读取与输出，旨在为读者建立起一个全面的R语言入门基础。

# 3. 描述性统计分析与图形展示

## 3.1 描述性统计分析

描述性统计是统计学中的一个基础分支，它涉及对数据集中趋势和离散程度的度量。集中趋势可以反映数据的一般水平或典型值，而离散程度则衡量数据的分散情况，反映了数据点与中心点的偏离程度。

### 3.1.1 集中趋势的度量

在统计分析中，集中趋势的度量通常包括三种：平均数、中位数和众数。

- **平均数（Mean）** 是所有数值加总后除以数值的数量。它是最常用的集中趋势度量方式，但在有异常值时可能会受到较大影响。
- **中位数（Median）** 是将数据集排序后位于中间位置的值。在分布不对称或者包含异常值的数据集中，中位数通常比平均数更加稳定。
- **众数（Mode）** 是数据集中出现次数最多的数值。它在分类数据中应用广泛，也适用于数值数据。

### 3.1.2 离散程度的度量

描述性统计分析的另一项重要任务是度量数据集的离散程度，常用的度量方法包括极差、方差和标准差等。

- **极差（Range）** 是数据集中的最大值和最小值之间的差，它简单但受极端值影响较大。
- **方差（Variance）** 是各数据与平均数差值的平方的平均值。方差越大，数据的离散程度越高。
- **标准差（Standard Deviation）** 是方差的平方根，它与原数据单位相同，便于解释。

## 3.2 R语言中的图形系统

R语言有着强大的图形绘制能力，是数据可视化的理想选择。R中的图形系统分为基础图形系统和高级图形系统，高级图形系统如ggplot2提供了更为复杂和美观的图形定制选项。

### 3.2.1 基本图形的创建

基础图形系统是R语言自带的图形包，可以直接使用`plot()`函数进行快速绘图。

# 示例代码：绘制数据x和y的散点图
x <- rnorm(100)
y <- x + rnorm(100, sd = 0.5)
plot(x, y)

上述代码首先创建了两个正态分布的随机变量x和y，然后使用`plot()`函数生成了它们的散点图。R语言的基础图形系统简单易用，适合快速生成一些标准图形。

### 3.2.2 高级图形定制

ggplot2是R中一个流行的图形包，它基于“图形语法”的概念，通过添加图层来定制图形。

# 示例代码：使用ggplot2绘制数据x和y的散点图，并添加拟合线
library(ggplot2)
df <- data.frame(x, y)
ggplot(df, aes(x = x, y = y)) +
  geom_point() +  # 添加散点图层
  geom_smooth(method = "lm")  # 添加线性回归拟合线层

在上述代码中，首先加载ggplot2包，然后创建一个数据框df，其中包含x和y的数据。`ggplot()`函数用于初始化图形，`aes()`函数设置绘图的美学映射，`geom_point()`添加散点层，`geom_smooth()`添加拟合线层。通过ggplot2，我们可以定制非常丰富的图形类型和细节。

在描述性统计分析之后，图形展示可以直观地传达数据集的特征，帮助我们更直观地理解和解释数据集。通过R语言，我们可以轻松地在基础和高级层面上定制和创建图形，无论是用于简单的探索性数据分析，还是用于准备发表的学术图表。

# 4. 多变量统计分析方法