Numpy.linalg在优化问题中的应用：线性和非线性规划问题的求解

# 1. Numpy.linalg库简介

## 1.1 Numpy库概述
Numpy是一个强大的Python库，专门用于进行大规模数值计算，尤其是在科学计算领域。它提供了高性能的多维数组对象以及用于处理这些数组的工具。

## 1.2 Numpy.linalg模块介绍
Numpy.linalg模块是Numpy库中专门用于线性代数计算的模块，包含了大量的线性代数运算函数，如矩阵乘法、求解线性方程组、计算矩阵的特征值等。

### 线性代数运算示例
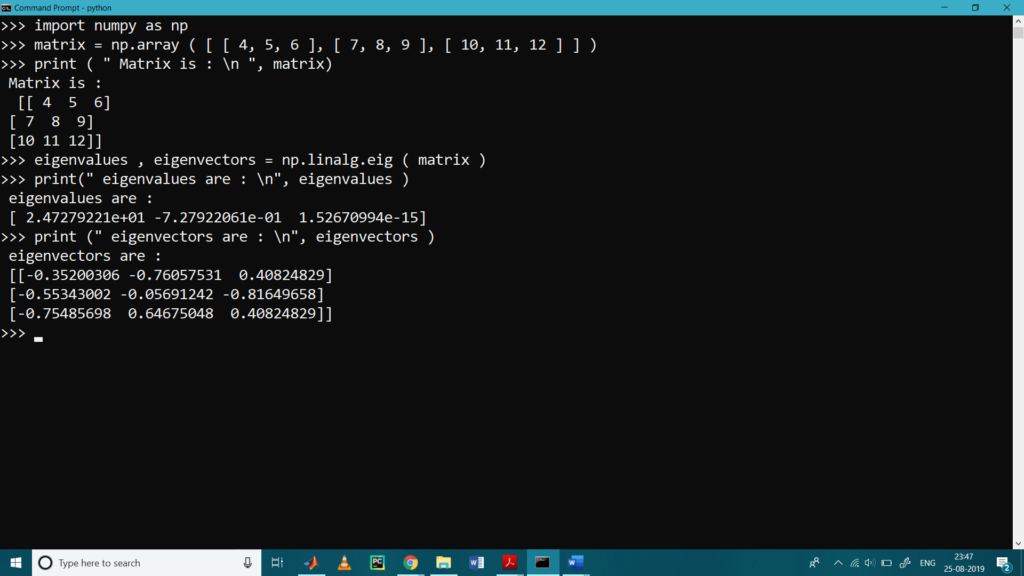
以下是一个简单的线性代数运算示例，展示如何使用Numpy.linalg模块计算矩阵的特征值和特征向量：

import numpy as np

# 创建一个矩阵
A = np.array([[1, 2], [3, 4]])

# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(A)

print("特征值:", eigenvalues)
print("特征向量:", eigenvectors)

在这个例子中，我们首先导入了Numpy库，并创建了一个2x2的矩阵A。然后使用`np.linalg.eig`函数计算了矩阵A的特征值和特征向量，并打印结果。

## 1.3 Numpy.linalg的应用场景
Numpy.linalg模块广泛应用于数据分析、机器学习、图像处理等领域，是进行线性代数计算不可或缺的工具。

通过本章的介绍，您将对Numpy.linalg模块有一个初步的了解，并掌握一些基本的操作。接下来的章节将深入探讨如何使用Numpy.linalg解决线性规划和非线性规划问题。

# 2. 线性规划问题的Numpy解法

在本章节中，我们将深入探讨如何使用Numpy.linalg库来解决线性规划问题。线性规划是运筹学中的一个重要分支，它在经济学、工程学、管理科学等领域有着广泛的应用。通过本章节的介绍，我们将了解线性规划的基础理论，并演示如何利用Numpy库中的线性代数工具来求解线性规划问题。

## 2.1 线性规划基础理论

### 2.1.1 线性规划的定义和数学模型

线性规划是研究在一组线性约束条件下，如何优化（最大化或最小化）某个线性目标函数的问题。它通常可以表示为以下数学模型：

maximize    c^T x
subject to  Ax <= b
            x >= 0

其中，`c` 是目标函数系数向量，`x` 是决策变量向量，`A` 是约束矩阵，`b` 是约束条件右侧的常数向量。我们的目标是找到一组 `x`，使得目标函数的值最大（或最小）。

### 2.1.2 线性规划的标准形式

线性规划的标准形式是指所有决策变量都是非负的，并且约束条件都是不等式。然而，在实际应用中，我们可能会遇到一些特殊情况，如等式约束或变量无非负限制的情况。这些问题可以通过引入松弛变量、剩余变量或人工变量转化为标准形式。

## 2.2 Numpy.linalg解决线性规划问题

### 2.2.1 利用矩阵运算求解线性规划

Numpy.linalg库提供了多种矩阵运算的功能，可以用来求解线性规划问题。最简单的方法是利用线性方程组的求解器，将线性规划问题转化为方程组求解。

#### 示例代码：

import numpy as np

# 目标函数系数
c = np.array([3, 2])

# 约束矩阵
A = np.array([[1, 2], [3, 1], [1, 1]])

# 约束条件右侧的常数向量
b = np.array([8, 18, 12])

# 利用线性方程组求解器求解
x = np.linalg.solve(A, b)

# 输出结果
print("决策变量x:", x)

#### 参数说明：

- `c`: 目标函数系数向量，表示为一个一维数组。
- `A`: 约束矩阵，表示为一个二维数组。
- `b`: 约束条件右侧的常数向量，表示为一个一维数组。

#### 执行逻辑说明：

上述代码中，我们首先定义了目标函数系数 `c` 和约束条件 `A`、`b`。然后，我们使用 `np.linalg.solve` 函数求解线性方程组 `Ax = b`，得到决策变量 `x` 的值。

#### 逻辑分析：

需要注意的是，这种方法只适用于不存在不等式约束的情况。对于包含不等式约束的线性规划问题，我们需要采用其他方法，如单纯形法或内点法等。

### 2.2.2 约束条件的处理和优化算法

在实际应用中，线性规划问题通常包含不等式约束。Numpy本身不提供直接求解包含不等式约束的线性规划问题的功能，但我们可以通过一些技巧来处理这些约束。

#### *.*.*.* 引入松弛变量

为了解决不等式约束，我们可以引入松弛变量将其转化为等式约束。例如，对于约束 `Ax <= b`，我们可以添加松弛变量 `s`，使得 `Ax + s = b`，其中 `s >= 0`。

#### *.*.*.* 单纯形法

单纯形法是一种常用的求解线性规划问题的算法，它通过在可行域的顶点之间移动来寻找最优解。Numpy.linalg库不包含单纯形法的实现，但我们可以使用`scipy.optimize.linprog`函数作为替代。

#### 示例代码：

from scipy.optimize import linprog

# 目标函数系数（负号表示最小化）
c = -np.array([3, 2])

# 约束矩阵
A = np.array([[1, 2], [3, 1], [1, 1]])

# 约束条件右侧的常数向量
b = np.array([8, 18, 12])

# 求解线性规划问题
res = linprog(c, A_ub=A, b_ub=b, bounds=(0, None), method='highs')

# 输出结果
print("最优解:", res.x)

#### 参数说明：

- `c`: 目标函数系数向量，由于`linprog`默认求最小值，因此这里使用负号表示最大化。
- `A_ub`: 不等式约束矩阵。
- `b_ub`: 不等式约束右侧的常数向量。
- `bounds`: 变量的界限，表示为`(最小值, 最大值)`的元组，这里我们限制第一个变量最小值为0。

#### 执行逻辑说明：

上述代码中，我们使用`scipy.optimize.linprog`函数来求解线性规划问题。我们首先定义了目标函数系数 `c` 和不等式约束 `A_ub`、`b_ub`，然后设置了变量的界限。最后，我们调用`linprog`函数求解，并输出最优解 `x`。

#### 逻辑分析：

`linprog`函数提供了多种求解线性规划问题的方法，包括单纯形法和内点法。在本例中，我们使用了`highs`方法，它是一种高性能的单纯形法实现。

## 2.3 实践案例分析

### 2.3.1 经济学中的资源优化案例

在经济学中，线性规划常用于资源的优化分配。例如，一个公司需要决定如何分配其资源以最大化利润。

#### 案例描述：

假设公司有两种产品A和B，生产产品A需要资源1和资源2，生产产品B只需要资源2。公司希望在资源限制下最大化利润。

#### 模型建立：

我们可以将问题表述为以下线性规划模型：

maximize    P_A * x_A + P_B * x_B
subject to  R1 * x_A <= R1_total
            R2 * x_A + R2 * x_B <= R2_total
            x_A, x_B >= 0

其中，`P_A` 和 `P_B` 分别是产品A和B的利润，`x_A` 和 `x_B` 是生产产品A和B的数量，`R1` 和 `R2` 是生产每种产品所需的资源量，`R1_total` 和 `R2_total` 是公司拥有的资源总量。

#### 求解过程：

我们可以通过定义目标函数和约束条件，然后使用`scipy.optimize.linprog`函数来求解这个线性规划问题。

### 2.3.2 工程问题中的应用实例

在工程领域，线性规划也可以用来优化设计和决策。例如，设计一个桥梁时，我们需要决定如何使用有限的材料来最小化成本或最大化结构的稳定性。

#### 案例描述：

假设我们需要设计一个桥梁，使用两种类型的材料M1