【Quartus 13.0新手速成】：从零开始的全加器设计与仿真秘籍


参考资源链接：[Quartus II 实验：1位全加器的原理图设计与仿真](https://wenku.csdn.net/doc/4gb6f4yfgn?spm=1055.2635.3001.10343)
# 1. Quartus 13.0全加器设计入门

全加器是数字电路设计中最基本的构件之一，它能够实现三个一位二进制数相加的功能，并输出一个和位以及一个进位位。在Quartus 13.0中设计全加器不仅可以帮助初学者理解数字逻辑电路，还可以作为进一步学习更复杂电路设计的基石。本章将引导读者通过Quartus 13.0这个强大的集成开发环境，完成一个全加器的设计过程。我们将从理解全加器的数字逻辑基础开始，逐步深入到使用Quartus软件进行全加器的绘制、编码和测试。通过本章的学习，读者应能熟练掌握使用Quartus 13.0设计简单数字电路的流程，并为接下来更深入的学习打下坚实的基础。

graph LR
A[开始全加器设计入门] --> B[了解数字逻辑基础]
B --> C[掌握Quartus 13.0使用]
C --> D[进行全加器设计]
D --> E[测试与调试全加器]
E --> F[完成全加器设计入门]

在接下来的章节中，我们将详细探讨全加器的数字逻辑基础，以及如何在Quartus 13.0中实现一个功能齐全的全加器设计，并最终应用到实际项目中去。

# 2. 全加器的数字逻辑基础

数字逻辑是构建现代电子系统的基石，它允许我们通过基本的逻辑门来创建复杂的电路。全加器作为一个基础的数字电路组件，在数字逻辑设计中扮演着重要的角色。在深入Quartus 13.0全加器设计实践之前，本章将详细介绍数字逻辑和布尔代数基础，全加器的理论构建以及其电路图的实现方法。

### 2.1 数字逻辑与布尔代数

#### 2.1.1 布尔代数的基本运算

布尔代数是一种用于处理逻辑运算的数学体系，它使用一系列的运算符来表示逻辑操作。布尔代数的基本运算包括逻辑与（AND）、逻辑或（OR）和逻辑非（NOT）。在数字逻辑设计中，这些基本运算被用来构建更复杂的逻辑电路。

- **逻辑与（AND）运算**：只有当所有输入都为真（1）时，输出才为真（1）。用符号表示为 `A AND B = C`。
- **逻辑或（OR）运算**：只要有任何一个输入为真（1），输出就为真（1）。用符号表示为 `A OR B = C`。
- **逻辑非（NOT）运算**：输入信号的逻辑反转。用符号表示为 `NOT A = C`。

#### 2.1.2 逻辑门及其应用

逻辑门是布尔代数运算的物理实现。在电子电路中，逻辑门用晶体管、二极管等构建。最常见的逻辑门有：

- **AND门**：其输出仅在所有输入为1时才为1。
- **OR门**：其输出在任一输入为1时即为1。
- **NOT门**：也称为反相器，它的输出总是输入的反面。

逻辑门可以串联或并联，形成更复杂的电路。例如，一个简单的组合逻辑电路可以由两个AND门和一个OR门组成，执行如下操作 `(A AND B) OR (A AND C)`。

### 2.2 全加器的理论构建

#### 2.2.1 全加器的功能描述

全加器是一种算术电路，能够实现三个位的加法，包括两个加数位和一个进位输入。全加器的输出包括一个和位（Sum）和一个进位输出（Carry Out）。全加器可以扩展为多位加法器，是构建复杂算术运算电路的基础。

#### 2.2.2 全加器的真值表和逻辑表达式

全加器的真值表描述了其所有可能输入（A、B、进位输入Ci）与其对应输出（和位S、进位输出Co）之间的关系。真值表如下所示：

| A | B | Ci | S (和位) | Co (进位输出) |
|---|---|----|----------|---------------|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |

基于真值表，我们可以得到全加器的和位和进位输出的逻辑表达式：

- S = A ⊕ B ⊕ Ci
- Co = (A AND B) OR (B AND Ci) OR (A AND Ci)

其中，⊕ 表示逻辑异或（XOR）运算。

### 2.3 全加器的电路图实现

#### 2.3.1 手动绘制全加器电路

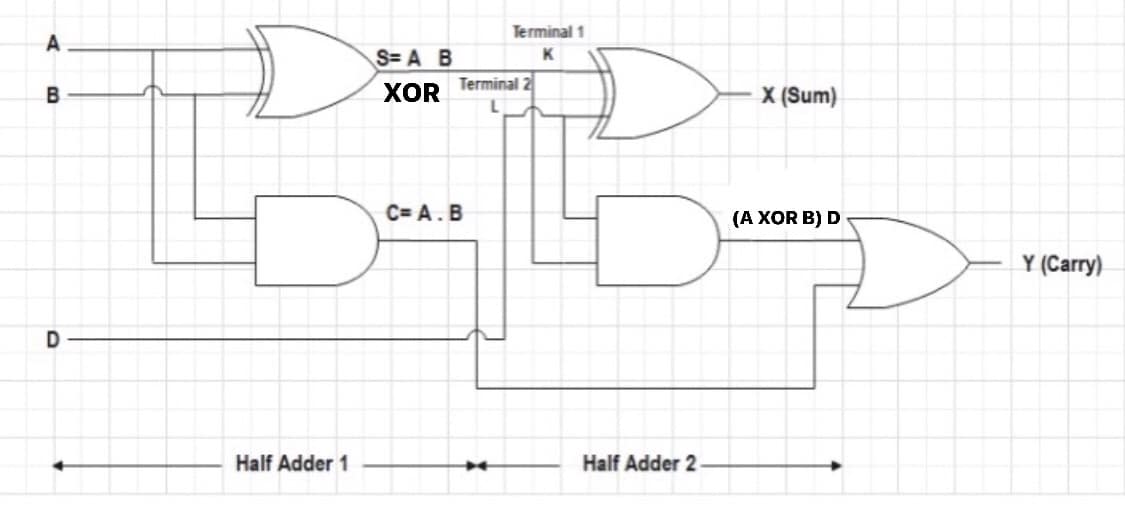
全加器的电路图可以手动绘制在纸上，也可以使用电路设计软件如Quartus来实现。手动绘制电路图时，需要根据逻辑表达式来放置逻辑门并连接它们。例如，使用两个XOR门实现和位，三个AND门和一个OR门实现进位输出。

#### 2.3.2 逻辑门简化技巧

在设计全加器电路时，可以使用一些简化技巧来减少所需的逻辑门数量。例如，全加器的进位输出Co可以通过Karnaugh图或Quine-McCluskey方法进行简化。简化后的逻辑表达式可以减少电路中的组合逻辑层次，从而提高电路的性能和减少所需的硬件资源。

graph TD;
    A((A)) -->|AND| G1((G1));
    B((B)) -->|AND| G1;
    B -->|AND| G2((G2));
    Ci((Ci)) -->|AND| G2;
    Ci -->|AND| G3((G3));
    A -->|AND| G3;
    G1 -->|OR| Co((Co));
    G2 -->|OR| Co;
    G3 -->|XOR| S((S));

在上述流程图中，A、B和Ci代表输入信号，S是和位输出，Co是进位输出。G1、G2和G3代表由输入信号组合生成的中间逻辑信号。从图中可以看出，通过逻辑门的优化排列，可以在不增加额外硬件的情况下实现全加器的所有功能。

在实际应用中，设计者需要通过反复测试和验证来确保电路设计的正确性和高效性。使用如Quartus这样的软件工具可以帮助设计者迅速地进行电路仿真和验证，以确保设计满足预期功能和性能要求。

# 3. Quartus 13.0全加器设计实践

## 3.1 Quartus 13.0环境设置

### 3.1.1 Quartus软件的安装与配置

在开始设计全加器之前，正确地安装和配置Quartus软件是至关重要的。Quartus Prime是由Altera公司（现已被Intel收购）开发的一款强大的FPGA开发环境，提供了从设计输入、编译、优化、仿真到硬件配置等一系列完整的解决方案。安装Quartus软件时，需要注意以下步骤和事项：

- **系统要求：** 首先确认计算机满足Quartus Prime的最低系统要求，包括操作系统版本、处理器速度、内存大小和硬盘空间。
- **软件下载：** 从Intel官方网站下载Quartus Prime最新版的安装文件。确保选择与您的操作系统相匹配的版本。
- **安装向导：** 运行安装程序，并遵循安装向导的指引完成安装。在安装过程中，可能会提示选择安装组件，建议保留所有默认设置以获取完整功能。
- **许可证注册：** 安装完成后，输入许可证文件，或者如果是学生版可以使用免费的许可。
- **配置环境变量：** 在Windows系统中，根据安装目录，配置环境变量，确保可以在命令行中直接调用Quartus工具。

完成上述步骤后，Quartus软件环境就设置好了。下一步是创建一个新的项目，并开始我们的全加器设计。

### 3.1.2 创建项目和文件结构

创建项目是设计流程的第一步，它将定义项目的结构和包含的文件类型。在Quartus中创建项目，需要按照以下步骤进行：

- **启动Quartus软件：** 打开Quartus软件，会看到一个启动界面，选择“Create a New Project”以新建项目。
- **项目名称和位置：** 输入项目名称，并选择项目存放的位置。项目名称应具有描述性，以反映项目内容。
- **设备选择：** 选择与您的目标FPGA或CPLD芯片相匹配的设备。为全加器设计，选择一款合适的Cyclone系列FPGA。
- **添加文件：** 接下来，添加项目所需的文件类型。全加器设计至少需要VHDL文件。
- **项目目录结构：** 在本地计算机上创建一个结构化的文件夹来存放项目文件。例如，可以创建一个名为"FullAdder"的文件夹，然后在其中再建立子文件夹如"Sources", "Simulations"等来分类存放不同类型的文件。

一旦项目创建完毕，就可以开始编写VHDL代码来实现全加器设计了。确保编写清晰、组织良好的代码，这有助于提高开发效率和后期维护。

## 3.2 全加器的VHDL编码实现

### 3.2.1 VHDL基础知识回顾

在深入编写全加器代码之前，回顾一下VHDL的基础知识是很有必要的。VHDL（VHSIC Hardware Description Language）是一种硬件描述语言，用于模拟数字系统。它提供了一种描述硬件功能和结构的方法，支持从高层次的行为级到物理设计的各个阶段。以下是VHDL编码中需要了解的基本概念：

- **实体（Entity）：** 定义了接口，包括输入输出端口。
- **架构（Architecture）：** 对实体进行功能描述，它是实体具体实现的地方。
- **信号（Signal）：** 用于在实体和架构内连接不同部分的线。
- **进程（Process）：** 用来描述硬件的时序行为，是顺序执行的一组语句。
- **组件（Component）和实例化（Instantiation）：** 用于模块化设计，组件代表可重用的模块，实例化则是在架构中引用这个组件。

掌握这些基本概念后，我们就能够编写出规范的VHDL代码来实现全加器。

### 3.2.2 编写全加器的VHDL代码

下面是一个简单的全加器的VHDL代码实现，它使用了两个输入位（A和B）以及一个进位输入（Cin），并产生一个和（Sum）和一个进位输出（Cout）：

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.STD_LOGIC_ARITH.ALL;
use IEEE.STD_LOGIC_UNSIGNED.ALL;

-- 定义实体
entity FullAdder is
    Port ( A : in STD_LOGIC;
           B : in STD_LOGIC;
           Cin : in STD_LOGIC;
           Sum : out STD_LOGIC;
           Cout : out STD_LOGIC);
end FullAdder;

-- 实现架构
architecture Behavioral of FullAdder is
begin
    -- 行为描述
    Sum <= A xor B xor Cin;
    Cout <= (A and B) or (B and Cin) or (A and Cin);
end Behavioral;

在上述代码中，我们定义了一个名为`FullAdder`的实体，该实体有两个输入端口`A`和`B`，一个进位输入端口`Cin`，两个输出端口`Sum`和`Cout`。在架构`Behavioral`中，我们使用`xor`和`and`操作符对输入信号进行组合，以计算`Sum`和`Cout`的值。

接下来是全加器设计中非常重要的一个步骤：仿真测试。通过仿真可以验证我们的VHDL代码是否按照预期工作，而无需在实际硬件上进行测试。

## 3.3 全加器的仿真测试

### 3.3.1 创建仿真文件和测试环境

仿真过程涉及到创建测试台（Testbench）文件，测试台用于模拟全加器模块的输入信号，并观察输出信号的变化，以便验证设计的正确性。在Quartus中创建一个测试台文件的步骤如下：

- **启动文本编辑器：** 在Quartus中，选择“File”菜单下的“New”来创建一个新的文本文件。
- **编写测试台代码：** 在新文件中，编写用于测试全加器模块的VHDL代码。测试台是一个无端口的架构，并实例化了被测试的全加器模块。

以下是一个简单的全加器测试台示例：

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.STD_LOGIC_ARITH.ALL;
use IEEE.STD_LOGIC_UNSIGNED.ALL;

entity Testbench is
-- 测试台无端口
end Testbench;

architecture Behavioral of Testbench is
    -- 实例化全加器模块
    signal A, B, Cin: STD_LOGIC := '0';
    signal Sum, Cout: STD_LOGIC;
begin
    -- 测试台逻辑
    uut: entity work.FullAdder
        port map (
            A => A,
            B => B,
            Cin => Cin,
            Sum => Sum,
            Cout => Cout
        );

    -- 测试过程
    process
    begin
        -- 测试向量
        A <= '0'; B <= '0'; Cin <= '0';
        wait for 10 ns;
        A <= '0'; B <= '0'; Cin <= '1';
        wait for 10 ns;
        A <= '0'; B <= '1'; Cin <= '0';
        wait for 10 ns;
        A <= '0'; B <= '1'; Cin <= '1';
        wait for 10 ns;
        A <= '1'; B <= '0'; Cin <= '0';
        wait for 10 ns;
        A <= '1'; B <= '0'; Cin <= '1';
        wait for 10 ns;
        A <= '1'; B <= '1'; Cin <= '0';
        wait for 10 ns;
        A <= '1'; B <= '1'; Cin <= '1';
        wait for 10 ns;
        wait; -- 无限等待，终止仿真
    end process;
end Behavioral;

在上述测试台代码中，我们定义了三个测试向量，它们分别对应于全加器的三个输入信号的所有可能组合。通过逐个改变这些输入信号的值，我们可以观察到输出信号是否正确。测试过程中，每组输入保持稳定一段时间（例如10纳秒），以便仿真工具能够记录和分析结果。

### 3.3.2 分析仿真结果和调试

在编写完测试台代码后，启动仿真并观察结果。在Quartus中，可以通过“Tools”菜单下的“Run Simulation Tool”选项来运行仿真。仿真工具将展示波形图，其中包括输入信号和输出信号的变化。

在分析仿真结果时，需要验证以下几点：

- **功能正确性：** 所有输入组合下的输出是否与预期的全加器真值表一致。
- **时序正确性：** 输出信号的变化是否与输入信号变化同步。
- **异常情况处理：** 例如输入信号的跳变可能会产生抖动或错误的输出。

如果发现仿真结果不符合预期，我们需要检查和调整VHDL代码，并重新进行仿真。代码调试是一个反复的过程，可能包括更改信号赋值、添加延时以及优化逻辑表达式等。

正确实现全加器后，我们可以继续探索更高级的设计技巧，如参数化设计和层次化设计，这些将使得全加器设计更加灵活和可重用。

本章节介绍的全加器设计实践，是基于Quartus 13.0环境和VHDL语言的基础入门。这些知识和技能对任何希望进入FPGA设计领域的人都是不可或缺的。随着经验的累积，开发者可以通过不断的实践来深化理解，最终设计出更为复杂和高效的数字电路。

# 4. 全加器设计的高级技巧

## 4.1 参数化全加器设计

### 4.1.1 参数化设计的概念与优势

参数化设计是一种在硬件描述语言（HDL）中定义模块参数的技术，允许设计者在不改变代码结构的情况下，通过参数值的不同配置来实现设计的可复用性和可扩展性。在Quartus 13.0环境下进行全加器设计时，参数化有以下几个显著优势：

- **可复用性**：参数化设计允许同一份代码在不同的全加器位宽下复用，无需为每种位宽都编写新的代码。
- **可维护性**：当需要修改设计时，只在一个地方修改参数即可，而不需要在多份代码中进行改动，极大地提高了维护效率。
- **灵活性**：通过改变参数值，设计者可以轻松适应不同的设计需求，如调整全加器的位宽以适应不同性能和复杂度的要求。

### 4.1.2 实现参数化全加器

以VHDL为例，全加器可以被设计为一个参数化的模块。下面是一个简单的参数化全加器实现的例子：

library IEEE;
use IEEE.STD_LOGIC_1164.ALL;

entity ParametricAdder is
    generic (
        N : natural := 8 -- 参数N定义了全加器的位宽
    );
    port (
        A, B : in std_logic_vector(N-1 downto 0); -- 两个N位输入向量
        Cin  : in std_logic; -- 进位输入
        Sum  : out std_logic_vector(N-1 downto 0); -- 求和结果
        Cout : out std_logic -- 进位输出
    );
end ParametricAdder;

architecture Behavioral of ParametricAdder is
begin
    -- 全加器的实现细节
    -- 使用迭代语句或生成语句（Generate Statement）来根据参数N实例化多个全加器模块
end Behavioral;

在上面的代码中，`generic`声明部分允许用户指定全加器的位宽`N`。参数`N`在实例化该实体时可以被指定，从而创建一个N位的全加器。这种设计方式保证了代码的通用性和灵活性。

## 4.2 全加器的层次化设计

### 4.2.1 模块化设计的重要性

模块化设计是将复杂系统分解为更小、更易于管理的模块的过程。在全加器设计中，层次化设计意味着将全加器划分为更小的单元，如半加器、全加器或其它逻辑模块。模块化设计有以下重要性：

- **简化设计流程**：模块化可以将大问题分解成小问题，简化了设计流程。
- **提高可读性**：清晰定义的模块边界有助于提高代码的可读性，新开发者更容易理解和参与项目。
- **便于调试与测试**：单个模块的错误更容易被定位和修复，测试也可以在模块级别上进行，降低了复杂性。

### 4.2.2 构建层次化的全加器设计

层次化设计通常通过封装和组合多个子模块来实现。在VHDL中，全加器的一个简单层次化实现可能包含以下模块：

1. **半加器（Half Adder）**：实现单个比特的加法。
2. **进位生成器（Carry Generator）**：计算进位。
3. **进位传播器（Carry Propagator）**：将进位从低位传递到高位。

代码示例和模块划分将根据具体实现和需求而定，但每一层模块都有明确的功能和接口。设计者可以通过模块化的思维将这些部件组合起来，最终构成一个完整的全加器。

## 4.3 优化全加器设计的性能

### 4.3.1 识别和改进设计瓶颈

全加器设计的性能瓶颈可能包括延迟、资源消耗和功耗。识别这些瓶颈是优化的第一步。在全加器设计中，延迟主要取决于逻辑门的级联深度和逻辑路径。资源消耗通常与使用的逻辑门和寄存器数量有关。功耗则与信号切换的频率和幅度相关。

### 4.3.2 性能优化策略和案例分析

性能优化策略可以包括但不限于：

- **减少逻辑级数**：通过逻辑优化技术，比如Karnaugh图，简化逻辑表达式，减少逻辑门的数量和级数。
- **使用查找表（LUT）**：对于复杂逻辑，使用查找表可以减少逻辑门数量。
- **流水线化**：在全加器设计中引入流水线结构，可以提高数据吞吐率，降低关键路径的延迟。
- **门控时钟技术**：对于时钟信号的管理，门控时钟可以减少不必要的功耗。

案例分析可能涉及特定设计改进前后的对比，以及所采用技术对性能的具体影响。通过案例，设计者可以了解各种优化技术的实际效果，从而更有效地应用于自己的设计中。

在本章节中，我们深入探讨了全加器设计的高级技巧，包括参数化设计、层次化设计以及性能优化策略。这些技巧不仅对设计一个简单的全加器有帮助，还可以扩展到更复杂的数字电路设计中去。下一章节中，我们将看到全加器在更复杂的电路中的应用，并对Quartus 13.0软件的未来展望有所讨论。

# 5. 全加器设计的项目应用与展望

在第四章中，我们深入探讨了全加器设计的高级技巧，包括参数化设计、层次化设计以及优化策略。在这一章中，我们将目光转向全加器设计的实际应用以及对Quartus 13.0和未来FPGA技术的展望。

## 5.1 全加器在复杂电路中的应用

全加器作为一种基础的数字电路构建块，在复杂电路设计中扮演着至关重要的角色。其主要应用场景包括算术逻辑单元（ALU）和处理器设计。

### 5.1.1 全加器在算术逻辑单元中的角色

算术逻辑单元是现代处理器的核心组成部分，负责执行所有的算术和逻辑操作。全加器在ALU中用于实现基本的算术运算，比如加法和进位。它是构建复杂算术运算的基本单元，如乘法和除法。

### 5.1.2 简单处理器中的全加器应用实例

一个简单的处理器设计可能包括多个全加器电路模块，以实现多级的加法操作。在处理器设计中，全加器通常需要与其他逻辑门电路结合，来实现如算术左移和逻辑右移等更复杂的操作。

// Verilog实现的4位全加器
module FourBitAdder(
    input [3:0] A,
    input [3:0] B,
    input Cin,
    output [3:0] Sum,
    output Cout
);
    wire C1, C2, C3;

    FullAdder FA0(
        .A(A[0]),
        .B(B[0]),
        .Cin(Cin),
        .Sum(Sum[0]),
        .Cout(C1)
    );

    FullAdder FA1(
        .A(A[1]),
        .B(B[1]),
        .Cin(C1),
        .Sum(Sum[1]),
        .Cout(C2)
    );

    FullAdder FA2(
        .A(A[2]),
        .B(B[2]),
        .Cin(C2),
        .Sum(Sum[2]),
        .Cout(C3)
    );

    FullAdder FA3(
        .A(A[3]),
        .B(B[3]),
        .Cin(C3),
        .Sum(Sum[3]),
        .Cout(Cout)
    );
endmodule

上述代码展示了一个4位全加器的Verilog实现，它由四个全加器模块构成，每个全加器处理一位，并通过进位链连结。

## 5.2 Quartus 13.0的未来展望

Quartus软件作为Intel FPGA设计的关键工具，随着技术的发展而不断更新，为FPGA设计者提供了越来越多的功能。

### 5.2.1 FPGA技术的发展趋势

随着FPGA技术的不断进步，未来FPGA将拥有更高的性能、更大的逻辑容量和更低的功耗。特别是在人工智能和机器学习领域，FPGA作为加速器的需求将不断增加。

### 5.2.2 Quartus软件新特性的期待

用户期待Quartus软件能够提供更加直观的设计流程、更强的优化算法以及更好的集成开发环境。此外，对于与云服务的整合、多FPGA协同设计支持等也是未来发展的潜在方向。

通过本章的介绍，我们可以看到全加器在电路设计中的关键作用，以及Quartus软件在未来技术中的重要地位。IT行业从业者不仅需要掌握全加器的设计和应用，还应该了解FPGA技术的最新发展动态，以便更好地适应未来的技术变革。