对数在统计学中的应用：正态分布和卡方分布，数据分析必备技能

# 1. 对数在统计学中的应用简介

对数在统计学中有着广泛的应用，它可以帮助我们处理各种类型的非正态数据。对数变换可以将非正态分布的数据转换为更接近正态分布的数据，从而简化统计分析和建模。

对数变换的优点包括：

- **稳定方差：**对数变换可以稳定数据的方差，使之更接近正态分布。
- **正态化分布：**对数变换可以将非正态分布的数据转换为更接近正态分布，从而简化统计推断。
- **减少异方差：**对数变换可以减少不同组别之间方差的差异，提高统计分析的准确性。

# 2. 正态分布的理论基础

正态分布，又称高斯分布，是统计学中最重要的连续概率分布之一，广泛应用于自然科学、社会科学和工程技术等领域。本章节将介绍正态分布的定义、性质、概率密度函数和累积分布函数。

### 2.1 正态分布的定义和性质

正态分布是一个连续概率分布，其概率密度函数由以下公式表示：

f(x) = (1 / (σ√(2π))) * exp(-(x - μ)² / (2σ²))

其中：

- μ 是正态分布的均值，表示分布的中心位置。
- σ 是正态分布的标准差，表示分布的离散程度。

正态分布具有以下性质：

- 对称性：正态分布曲线关于均值对称。
- 钟形：正态分布曲线呈钟形，两端逐渐衰减。
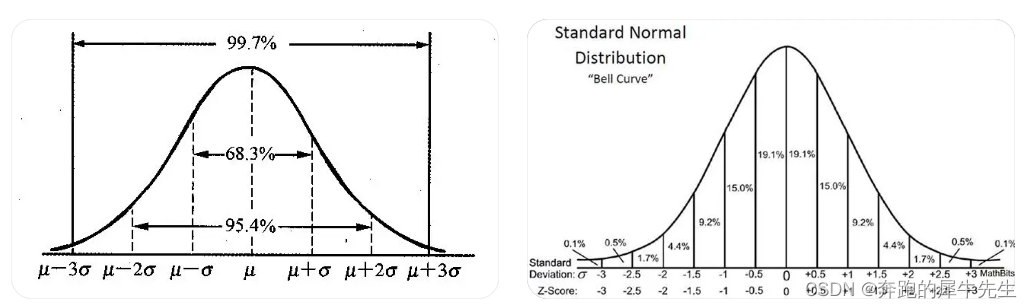
- 68-95-99.7 法则：在均值两侧的一个标准差范围内包含约 68% 的数据，两个标准差范围内包含约 95% 的数据，三个标准差范围内包含约 99.7% 的数据。

### 2.2 正态分布的概率密度函数

正态分布的概率密度函数描述了在给定值 x 处观察到该值的概率。其公式如下：

f(x) = (1 / (σ√(2π))) * exp(-(x - μ)² / (2σ²))

其中：

- x 是随机变量的值。
- μ 是正态分布的均值。
- σ 是正态分布的标准差。

### 2.3 正态分布的累积分布函数

正态分布的累积分布函数 (CDF) 表示在给定值 x 处观察到小于或等于该值的概率。其公式如下：

F(x) = ∫_{-\∞}^{x} (1 / (σ√(2π))) * exp(-(t - μ)² / (2σ²)) dt

其中：

- x 是随机变量的值。
- μ 是正态分布的均值。
- σ 是正态分布的标准差。

累积分布函数可以用于计算给定值 x 以下的概率。

# 3.1 正态分布的抽样和参数估计

**3.1.1 抽样分布**

从正态分布总体中抽取样本，样本均值的分布也是正态分布，称为正态分布的抽样分布。抽样分布的均值等于总体均值，标准差为总体标准差除以样本容量的平方根。

**公式：**

X̄ ~ N(μ, σ/√n)

其中：

* X̄ 为样本均值
* μ 为总体均值
* σ 为总体标准差
* n 为