层次聚类算法在生物信息学中的应用：基因组分析与药物发现的利器

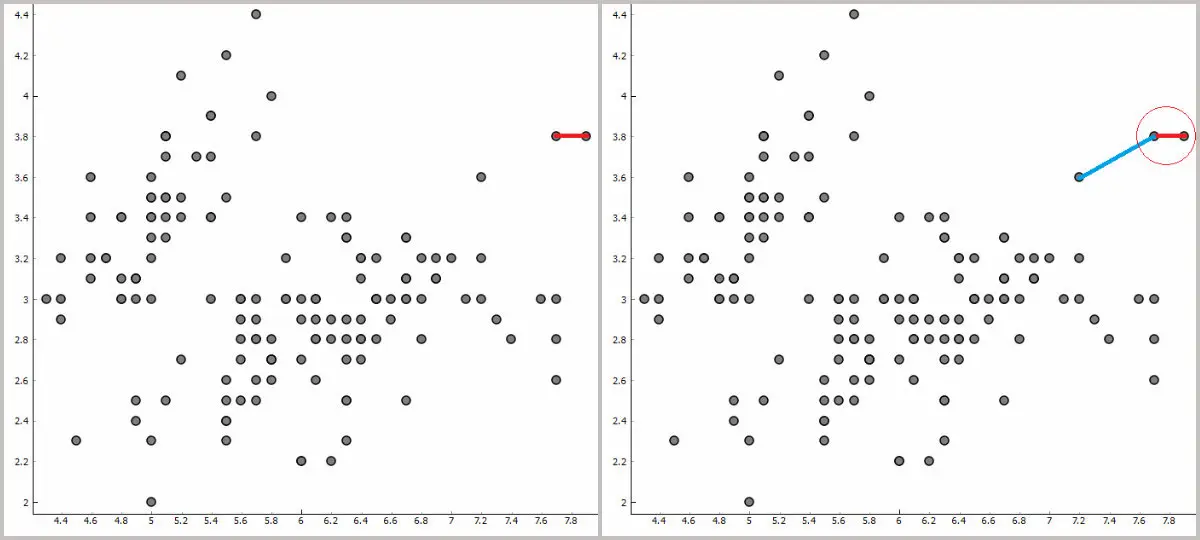
# 1. 层次聚类算法简介**

层次聚类算法是一种无监督机器学习算法，用于识别数据中的自然分组。它将数据点逐步合并到嵌套的层次结构中，称为树状图或层次树。层次聚类算法的特点是：

- **层次性：**算法以自下而上的方式进行，从单个数据点开始，逐步合并形成更大的簇。
- **可视化：**树状图提供了一个直观的表示，显示了簇之间的关系和层次结构。
- **灵活性：**算法可以根据不同的相似性度量和链接准则进行定制，以适应不同的数据集。

# 2. 层次聚类算法在基因组分析中的应用

层次聚类算法在基因组分析中发挥着至关重要的作用，它可以识别基因表达模式、组装基因组序列以及识别生物标记物和疾病亚型。

### 2.1 基因表达谱聚类

基因表达谱聚类是将具有相似表达模式的基因分组的过程。它有助于识别基因组中的功能模块，例如信号通路、代谢途径和转录调控网络。

**操作步骤：**

1. 收集基因表达数据（例如，RNA-Seq或微阵列数据）。
2. 对数据进行预处理（例如，归一化和对数变换）。
3. 使用层次聚类算法（例如，平均连锁或沃德法）对基因进行聚类。
4. 可视化聚类结果（例如，热图或树状图）。

**代码示例：**

import numpy as np
import scipy.cluster.hierarchy as sch

# 加载基因表达数据
data = np.loadtxt('gene_expression_data.csv', delimiter=',')

# 预处理数据
data = np.log2(data + 1)

# 执行层次聚类
linkage_matrix = sch.linkage(data, method='average')

# 可视化聚类结果
sch.dendrogram(linkage_matrix, labels=['Gene 1', 'Gene 2', ...])

**逻辑分析：**

* `linkage()` 函数使用平均连锁法计算连锁矩阵。
* `dendrogram()` 函数生成树状图，显示基因之间的聚类关系。

### 2.2 基因组序列聚类

基因组序列聚类用于组装基因组序列、识别重复序列和比较不同物种的基因组。

**操作步骤：**

1. 收集基因组序列数据（例如，来自测序平台的 FASTQ 文件）。
2. 对序列进行预处理（例如，修剪和拼接）。
3. 使用层次聚类算法（例如，单连锁或邻接法）对序列进行聚类。
4. 可视化聚类结果（例如，凝结树）。

**代码示例：**

import Bio.SeqIO
import Bio.Cluster

# 加载基因组序列
sequences = [record.seq for record in Bio.SeqIO.parse('genome_sequences.fasta', 'fasta')]

# 预处理序列
sequences = [seq.upper().replace('N', '') for seq in sequences]

# 执行层次聚类
cluster = Bio.Cluster.hierarchy(sequences, method='single')

# 可视化聚类结果
Bio.Cluster.draw_dendrogram(cluster, labels=['Sequence 1', 'Sequence 2', ...])

**逻辑分析：**

* `hierarchy()` 函数使用单连锁法计算层次聚类。
* `draw_dendrogram()` 函数生成凝结树，显示序列之间的聚类关系。

### 2.3 识别生物标记物和疾病亚型

层次聚类算法可以识别基因表达谱或基因组序列中的模式，从而识别生物标记物和疾病亚型。

**操作步骤：**

1. 收集患者样本的基因组数据。
2. 对数据进行预处理和聚类（如上所述）。
3. 识别聚类组之间的差异表达基因或序列变异。
4. 验证差异表达基因或序列变异与疾病表型的关联。

**表格：层次聚类算法在基因组分析中的应用**

| 应用 | 目的 | 数据类型 | 算法 | 输出 |
|---|---|---|---|---|
| 基因表达谱聚类 | 识别基因功能模块 | RNA-Seq 或微阵列数据 | 平均连锁、沃德法 | 热图、树状图 |
| 基因组序列聚类 | 组装基因组序列、识别重复序列 |