MATLAB遗传算法vs元启发式算法：优势对比与应用策略

# 1. 遗传算法与元启发式算法概述

遗传算法与元启发式算法是解决复杂优化问题的有力工具，它们在IT领域及相关的工程问题中扮演着重要角色。本章将对这两种算法的概念、特点以及它们在行业中的应用进行概述。

## 1.1 算法的定义和用途

遗传算法（Genetic Algorithm, GA）是一种模拟自然选择和遗传学机制的搜索算法，它属于元启发式算法的一种。由于其独特的全局搜索能力和相对简单的实现方式，遗传算法广泛应用于函数优化、机器学习、控制工程和调度等领域。

## 1.2 算法的发展背景

遗传算法的发展受到生物学中自然选择理论的启发。1975年，美国计算机科学家John Holland教授提出了遗传算法的基础理论，此后，这一算法不断被改进并应用到更多的领域。元启发式算法，如遗传算法，是为了解决NP-hard问题而诞生的一类算法。NP-hard问题的特点是，随着问题规模的增大，寻找最优解所需的时间会指数级增长。

## 1.3 算法的行业影响

在IT行业内，遗传算法与元启发式算法提供了新的解决方案来优化性能，提高效率。例如，通过遗传算法优化代码，能够显著减少程序的运行时间。在工程领域，它们被用于设计更有效的交通调度系统、电网管理，甚至在游戏设计中用于创造出更具挑战性的AI对手。

总的来说，遗传算法和元启发式算法是值得深入研究和实践的领域，其在提升算法效率和解决复杂问题中发挥着不可忽视的作用。在接下来的章节中，我们将详细探讨遗传算法的基础理论、实现步骤以及它们在工程和科学研究中的具体应用。

# 2. ```
# 第二章：遗传算法基础理论与实践

## 2.1 遗传算法核心概念

### 2.1.1 遗传算法的工作原理

遗传算法（Genetic Algorithm, GA）是一种模拟自然选择和遗传机制的搜索优化算法，由John Holland及其同事们在1975年提出。其工作原理主要模仿了生物进化过程中的“适者生存，优胜劣汰”的规律。遗传算法将问题的潜在解编码为一系列的串结构，这些串结构常被视作“染色体”，而串中的每个元素则对应“基因”。

算法初始化时，随机生成一组“种群”（也就是一组潜在的解决方案）。通过选择（Selection）、交叉（Crossover）和变异（Mutation）这三种主要操作，种群中表现较好的个体被保留下来，并产生新的后代。这个过程会重复迭代，直至达到预设的终止条件，最终解（最优解或近似最优解）被找到。

遗传算法的优势在于能够在较大的搜索空间中有效进行全局搜索，并且在复杂问题中，具有较好的鲁棒性和通用性。

### 2.1.2 遗传算法的关键组成部分

遗传算法的关键组成部分包括：

- **种群（Population）**：一组候选解的集合。
- **个体（Individual）**：种群中的每一个候选解，通常用字符串表示。
- **适应度函数（Fitness Function）**：衡量个体适应环境能力的函数，解的优劣由它决定。
- **选择（Selection）**：决定哪些个体能够遗传到下一代的过程。
- **交叉（Crossover）**：将两个个体的部分基因结合产生新个体的过程。
- **变异（Mutation）**：随机改变个体中某些基因的值以引入新的遗传信息。
- **终止条件（Termination Condition）**：决定算法何时停止的条件，如达到最大迭代次数或满足适应度阈值。

## 2.2 遗传算法的实现步骤

### 2.2.1 初始化种群

初始化种群是遗传算法的第一步，通常情况下，种群是随机生成的。种群中个体的数量被称为种群大小（Population Size），是遗传算法的一个关键参数，需要根据问题的复杂性和计算资源合理选择。

初始化种群的伪代码如下：

Population = []
For i = 1 to PopulationSize do
    Individual = GenerateRandomIndividual()
    Population.add(Individual)
EndFor

这里的`GenerateRandomIndividual()`函数负责根据问题的编码方式生成随机个体。

### 2.2.2 选择、交叉和变异操作

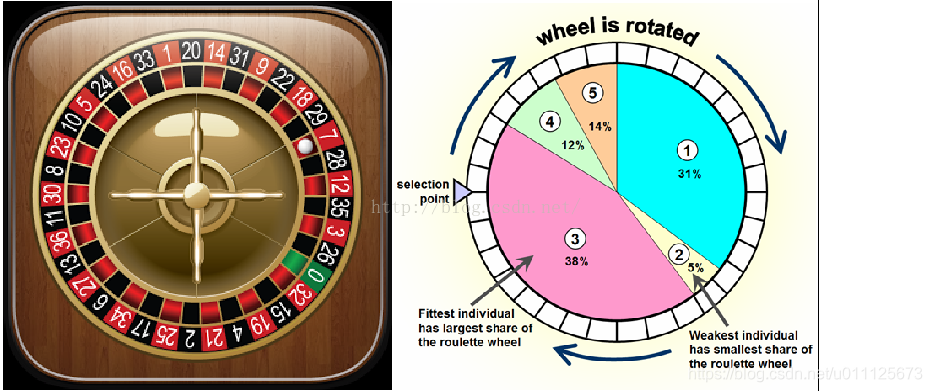
在遗传算法中，选择操作的目的是从当前种群中选择优秀的个体遗传到下一代。常见的选择方法包括轮盘赌选择（Roulette Wheel Selection）和锦标赛选择（Tournament Selection）。

交叉操作是遗传算法中模拟生物染色体交叉的主要环节，它随机配对种群中的个体，然后交换它们的部分基因片段。

变异操作随机改变个体中的某些基因，以维持种群的多样性并避免算法过早收敛到局部最优解。

### 2.2.3 算法终止条件与结果评估

遗传算法的终止条件可以是达到一定的迭代次数、找到足够好的解或是适应度提升幅度低于某个阈值。在每一代结束时，算法都会评估种群中每个个体的适应度，并根据适应度值进行选择、交叉和变异操作。

伪代码表示如下：

While not TerminationCondition() do
    SelectedIndividuals = Selection(Population)
    Offspring = Crossover(SelectedIndividuals)
    Offspring = Mutation(Offspring)
    Population = Combine(Population, Offspring)
    EvaluateFitness(Population)
EndWhile

在上面的伪代码中，`TerminationCondition()`函数根据设定的终止条件判断算法是否继续迭代。`Selection()`、`Crossover()`、`Mutation()`函数分别执行选择、交叉和变异操作。`EvaluateFitness()`函数负责计算种群中每个个体的适应度。

## 2.3 遗传算法的编码和解码策略

### 2.3.1 二进制编码

二进制编码是最常用的遗传算法编码方式之一。在这种方式下，问题的解被编码为一串0和1组成的二进制字符串。二进制编码简单直观，适用于许多优化问题，但也有一些局限性，比如在表示实数时可能会有精度问题。

### 2.3.2 浮点数编码

浮点数编码使用实数来表示染色体上的基因。这种编码方式可以提供更高的精度，并且在一些问题中能直接对应到问题的参数，使用起来更为直观和方便。

### 2.3.3 编码与解码的实践案例分析

在实践中，编码和解码策略需要根据具体问题进行选择。比如，对于一个旅行商问题（TSP），二进制编码可能需要额外的解码步骤将基因映射到城市访问序列，而实数编码则可以直观地表示城市间的距离。

| 编码类型 | 优点 | 缺点 | 适用问题 |
|----------|------|------|----------|
| 二进制编码 | 直观、简单、易于实现 | 精度有限，解码过程可能复杂 | 需要离散编码的问题 |
| 浮点数编码 | 高精度、表示直观 | 实现相对复杂 | 需要连续参数的问题 |

以浮点数编码为例，一个简单的遗传算法代码实现如下：

import numpy as np

# 假设问题的解由三个实数参数组成
def generate_individual():
    return np.random.rand(3)

# 适应度函数，根据问题定义
def fitness(individual):
    # 示例适应度计算
    return -sum(individual ** 2)

# 交叉操作
def crossover(parent1, parent2):
    alpha = np.random.rand()
    return alpha * parent1 + (1 - alpha) * parent2

# 变异操作
def mutate(individual, mutation_rate):
    if np.random.rand() < mutation_rate:
        idx = np.random.randint(0, len(individual))
        individual[idx] += np.random.randn()
    return individual

# 遗传算法主程序
def genetic_