MATLAB遗传算法解决调度问题：实战策略与案例探讨

# 1. 遗传算法与调度问题概述

## 1.1 遗传算法简介
遗传算法（Genetic Algorithms, GA）是一种模拟自然选择和遗传学机制的搜索优化算法。自提出以来，它在各种复杂系统的优化问题中被广泛应用，成为解决调度问题等NP难问题的有效工具。

## 1.2 调度问题的挑战
调度问题本质上是资源分配问题，涉及将有限资源在特定时间分配给多个任务。随着问题规模的增大，可能的解空间呈指数级增长，使得传统优化方法无法高效找到最优解。

## 1.3 遗传算法与调度问题的结合
通过遗传算法的优化能力，可以系统地遍历可能的调度方案，高效寻找到近似最优解。这种算法的迭代过程与调度问题的解空间探索非常契合，尤其在处理多目标和动态变化的调度问题时展现出独特优势。

graph LR
A[调度问题] -->|需要优化| B[遗传算法]
B -->|提供解决方案| A

遗传算法与调度问题的结合不仅限于理论，也扩展到实际应用场景，如生产制造、物流管理、医院排班等领域。在接下来的章节中，我们将深入探讨遗传算法的理论基础、在MATLAB平台上的应用，以及在不同调度问题中的实战策略和案例分析。

# 2. 遗传算法基本理论

### 2.1 遗传算法的基本原理

遗传算法（Genetic Algorithm, GA）是一种受自然选择和遗传学原理启发的搜索和优化算法，它模拟生物进化的过程来解决优化问题。我们首先需要了解其起源与发展，以及核心概念，从而为深入学习遗传算法打下基础。

#### 2.1.1 遗传算法起源与发展
遗传算法最初由美国计算机科学家约翰·霍兰德（John Holland）在20世纪70年代提出。他的研究初衷是寻求一种可以自动适应和改进的算法，模仿自然界生物的遗传和进化过程。霍兰德及其学生们开发了GA的基本理论，定义了遗传算法中的基本概念，如染色体、基因和适应度函数，并设计了选择、交叉和变异等遗传操作。

随着研究的深入，遗传算法在各个领域得到广泛应用，尤其是工程优化、人工智能和机器学习领域。80年代至90年代，随着计算机科学的飞速发展，遗传算法的计算能力得以提升，处理更复杂问题成为可能。到了21世纪，遗传算法已经发展成为解决复杂优化问题的一个重要工具。

#### 2.1.2 遗传算法的核心概念
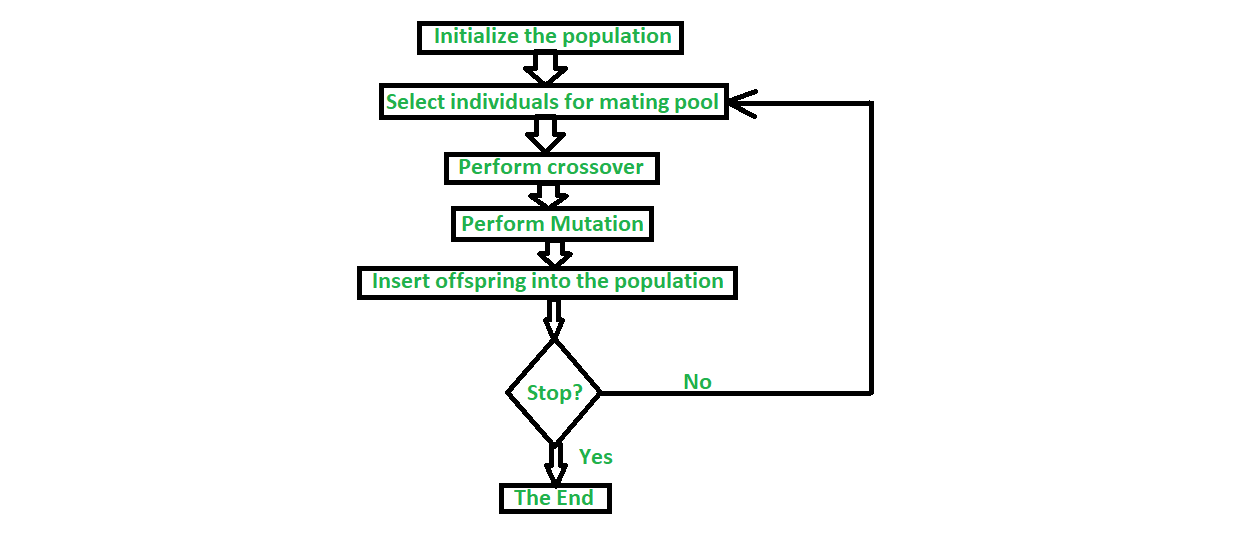
遗传算法的核心是模拟生物进化中的自然选择、交叉（杂交）和变异过程，通过迭代选择优秀的个体进行繁衍后代。在这个过程中，算法不断地寻找问题的最优解。核心概念包括：

- **染色体（Chromosome）**：代表问题的一个解决方案。
- **基因（Gene）**：染色体中的一个元素，它影响染色体表现出来的特征。
- **种群（Population）**：一组候选解的集合。
- **选择（Selection）**：根据个体的适应度，选择较好的个体进行繁衍后代。
- **交叉（Crossover）**：通过交换父母染色体的部分基因生成子代。
- **变异（Mutation）**：随机改变染色体上的某些基因，以增加种群的多样性。
- **适应度函数（Fitness Function）**：衡量某个解好坏的标准。

### 2.2 遗传算法的数学模型

要深入理解遗传算法，必须了解它的数学模型。这部分内容包括种群、个体和基因的概念，适应度函数的设计，以及遗传操作中的选择、交叉和变异。

#### 2.2.1 种群、个体和基因的概念

遗传算法操作的对象是种群中的个体，每个个体由一系列基因组成，基因在遗传算法中就是数据编码的基本单位。以二进制编码为例，基因可以是一串0和1的序列。

种群是遗传算法搜索空间的表示，每个个体都是空间中的一个点，代表了一个潜在的解决方案。算法开始时随机生成一个种群，随后通过选择、交叉和变异等操作，对种群进行迭代进化。

#### 2.2.2 适应度函数的设计

适应度函数是评价个体适应环境能力的标准，它根据问题的要求来衡量个体的表现好坏。在优化问题中，适应度函数通常与目标函数相同或相关。设计一个好的适应度函数至关重要，因为它是影响算法性能的关键因素之一。

适应度函数的设计应当符合以下原则：

- **简洁性**：易于计算，以保证算法的高效性。
- **准确性**：能够准确反映个体的优劣。
- **鲁棒性**：对于算法的稳定运行提供保障，避免由于适应度误差导致的不必要选择。

#### 2.2.3 遗传操作：选择、交叉和变异

遗传算法通过选择（Selection）、交叉（Crossover）和变异（Mutation）三种基本操作来实现对个体的遗传和进化。

- **选择**：通过适应度函数评价种群中的个体，并根据评价结果选择出优秀的个体作为后代的父母。选择的方式有很多种，比如轮盘赌选择、锦标赛选择等。
- **交叉**：交叉操作是遗传算法中产生新个体的主要方式，通常通过交叉点分割父母的基因片段，并以某种方式组合它们，生成子代。如单点交叉、多点交叉等。
- **变异**：为了增加种群的遗传多样性，防止算法早熟收敛，变异操作通过随机改变个体的某些基因来引入新的遗传信息。

### 2.3 遗传算法的实现技术

实现遗传算法除了理解其基本原理和数学模型外，还需要掌握具体的技术实现细节，主要包括参数设置以及算法的收敛性和多样性保持策略。

#### 2.3.1 参数设置：种群大小、交叉率和变异率

在遗传算法中，参数设置对于算法的性能有很大影响，主要包括种群大小、交叉率和变异率等：

- **种群大小（Population Size）**：种群中个体的数量。较大的种群可以提高找到全局最优解的概率，但会增加计算成本。
- **交叉率（Crossover Rate）**：执行交叉操作的概率。较高的交叉率可以增加种群的多样性，但过高的交叉率可能会破坏优秀个体的结构。
- **变异率（Mutation Rate）**：执行变异操作的概率。适当的变异率可以帮助算法跳出局部最优解，但过高的变异率可能会导致搜索过程变得随机。

#### 2.3.2 算法的收敛性和多样性保持策略

**收敛性**是指遗传算法能够有效地收敛到问题的最优解。而**多样性**保证了种群中个体的差异，防止算法早熟收敛于局部最优解。

为了提高算法的收敛性，常用策略包括：

- **精英保留策略**：保留一部分适应度最高的个体，不参与交叉和变异操作，直接进入下一代种群。
- **自适应交叉率和变异率**：根据种群的