MATLAB遗传算法函数优化：高效实现的四大方法

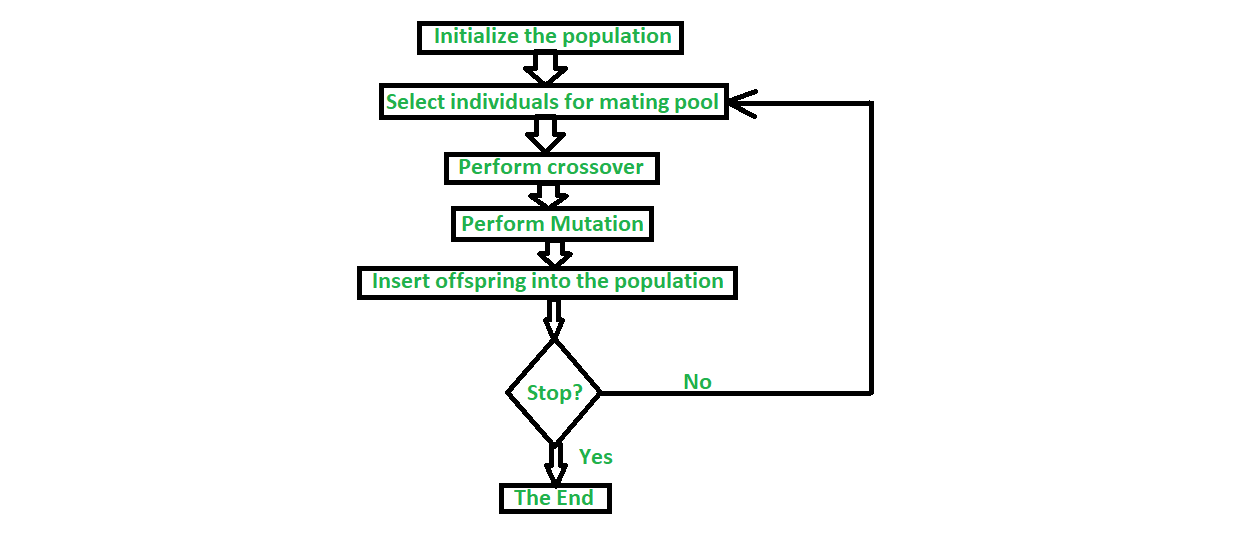
# 1. 遗传算法的基础理论

遗传算法是一种模拟自然选择和遗传学的优化算法，它们在解决优化和搜索问题中表现出色，因为它们能在广泛的搜索空间中有效地定位到高质量的解决方案。该算法的精髓在于使用概率的进化过程，来引导搜索朝着潜在的最优区域前进。遗传算法基于“适者生存”的原则，其中每个解决方案都被视为一个个体，通过选择、交叉和变异等操作，个体适应度会被评估，并且经过多代的迭代后，群体逐渐进化成越来越优的状态。

## 2.1 遗传算法的基本组成
遗传算法由以下基本组成部分构成：

### 2.1.1 初始化种群
遗传算法的初始化过程涉及到生成初始种群，即一系列随机创建的候选解决方案。种群中每一个个体被称为染色体，通常用二进制串、实数或其它编码方式来表示。初始化种群的质量对算法性能至关重要。

### 2.1.2 选择机制
选择机制是一种基于个体适应度进行“繁殖”的过程。高适应度的个体有更高的几率被选中并传递其基因给下一代。常用的选择算法包括轮盘赌选择、锦标赛选择等。

### 2.1.3 交叉与变异策略
交叉（杂交）是遗传算法中模拟生物遗传的重要步骤，通过选择两个父代个体并交换它们的部分基因来产生新的后代。变异策略则是引入随机性，以避免算法早熟收敛于局部最优解，通常是随机地改变个体中的某些基因。

遗传算法的理论基础为我们提供了强大的工具，以探索复杂的优化问题。在下一章中，我们将深入探讨MATLAB中遗传算法的具体实现框架，并提供代码示例和参数配置建议。

# 2. MATLAB遗传算法的实现框架

遗传算法作为模拟自然选择和遗传学机制的搜索算法，是优化问题中的一大利器。在MATLAB这一强大的数学计算平台上，实现遗传算法不仅有现成的工具箱支持，而且用户也可以自定义许多细节，以适应各种优化问题的需求。本章节将详细介绍MATLAB中遗传算法的实现框架，从基本组成到函数应用，再到适应度函数的设计，逐步深入，旨在帮助IT领域的高级从业者更好地理解和应用这一算法。

### 2.1 遗传算法的基本组成

#### 2.1.1 初始化种群

遗传算法的第一步是初始化一个种群，即一组潜在的解决方案。在MATLAB中，种群可以通过随机生成来初始化。这些解通常被编码为一串数字，代表可能的解空间中的点。

% MATLAB代码示例：初始化种群
popSize = 100; % 种群大小
chromLength = 30; % 染色体长度
pop = randi([0, 1], popSize, chromLength); % 生成一个popSize×chromLength的矩阵

在上面的MATLAB代码中，`randi` 函数生成了一个矩阵`pop`，其中每一行代表一个个体，每个个体由`chromLength`个基因组成。基因的取值范围是0到1，这适用于二进制编码的情况。

#### 2.1.2 选择机制

选择机制的目的是为了决定哪些个体将被保留到下一代。MATLAB中可以使用轮盘赌选择、锦标赛选择等方法。轮盘赌选择根据个体适应度的大小决定其被选择的概率。

% MATLAB代码示例：轮盘赌选择
fitness = sum(pop, 2); % 计算种群中每个个体的适应度
selected = rouletteWheelSelection(fitness); % 选择操作

在实际实现中，`rouletteWheelSelection` 是一个自定义函数，根据个体的适应度来赋予不同的选择概率，并模拟抽签选出下一代个体。

#### 2.1.3 交叉与变异策略

交叉（Crossover）和变异（Mutation）是遗传算法中生成新个体的两种主要方法。交叉是指两个个体根据某种方式交换基因片段，而变异则是随机改变个体中的某些基因。

% MATLAB代码示例：交叉与变异
children = crossover(pop); % 交叉操作
mutatedChildren = mutate(children); % 变异操作

在上述代码段中，`crossover` 和 `mutate` 函数分别模拟交叉和变异过程，对当前种群中的个体进行操作，从而产生下一代种群。

### 2.2 MATLAB中的遗传算法函数

#### 2.2.1 函数概述

MATLAB遗传算法工具箱提供了一些预定义的函数，这些函数用于优化问题的求解。最重要的函数之一是`ga`函数，它可以用来解决无约束或有约束的非线性优化问题。

% MATLAB代码示例：使用ga函数求解优化问题
[x, fval] = ga(fun, nvars, A, b, Aeq, beq, lb, ub, nonlcon, options);

其中参数意义如下：
- `fun`：目标函数。
- `nvars`：目标函数变量的数量。
- `A`、`b`、`Aeq`、`beq`：线性约束。
- `lb`、`ub`：变量的上下界。
- `nonlcon`：非线性约束。
- `options`：设置算法参数的结构体。
- `x`：返回的最优解。
- `fval`：返回的最优解的目标函数值。

#### 2.2.2 参数解析与配置

在MATLAB中，可以通过`optimoptions`函数来配置`ga`函数的各种参数。例如，可以设置种群大小、交叉概率、变异概率等。

% MATLAB代码示例：配置ga函数参数
options = optimoptions('ga', 'PopulationSize', 150, 'CrossoverFraction', 0.8, 'MutationRate', 0.01, 'Display', 'iter');

通过上述代码配置的参数，将影响遗传算法的搜索能力和收敛速度。细致地调整这些参数是优化遗传算法性能的关键。

### 2.3 遗传算法的适应度函数设计

#### 2.3.1 适应度函数的作用

适应度函数是评估个体好坏的标准，它决定了个体被选中繁衍后代的可能性。在MATLAB中，适应度函数应该定义为一个接受染色体作为输入，并返回一个适应度值作为输出的函数。

% MATLAB代码示例：定义适应度函数
function f = fitnessFunction(chromosome)
    % 解码染色体得到问题参数
    decodedParams = decodeChromosome(chromosome);
    % 计算目标函数值
    f = objectiveFunction(decodedParams);
end

适应度函数的设计需要与实际问题紧密相关，通常会利用问题领域的先验知识来优化。

#### 2.3.2 设计高效适应度函数的要点

设计适应度函数时需要注意以下几点：
- 函数应该能够准确反映个体的优劣。
- 应该尽可能简单，以减少计算时间。
- 在可能的情况下，避免出现0适应度值，这可能导致算法无法继续进化。

% MATLAB代码示例：避免0适应度的适应度函数
function f = safeFitnessFunction(chromosome)
    % 对目标函数值进行平滑处理
    rawFitness = fitnessFunction(chromosome);
    f = max(rawFitness, eps); % eps是MATLAB中的一个极小值
end

通过上述方法，可以确保所有的个体都有一定的生存机会，使得遗传算法能够更稳健地进行探索。

在本节中，通过介绍MATLAB遗传算法的框架，为读者提供了从种群初始化、选择、交叉、变异操作到遗传算法函数使用，以及适应度函数设计的完整流程。这些内容为使用MATLAB解决优化问题提供了理论基础和实际操作的方法，为后续章节中对遗传算法更深层次的探讨和应用打下了坚实的基础。

# 3. MATLAB遗传算法的高级技巧

## 3.1 优化问题的编码策略

### 3.1.1 二进制编码与实数编码
在遗传算法中，编码策略是将问题的解以某种方式表示为染色体结构，从而使得遗传操作（选择、交叉和变异）可以在这类结构上执行。编码策略的选择对算法性能有着决定性的影响。常用的编码策略包括二进制编码和实数编码。

二进制编码是最经典的编码方式，它将每个决策变量转换成一串二进制位，通过0和1的组合表示各种可能的决策变量值。例如，在0和1之间的实数变量，可以转换为二进制序列，然后通