MATLAB遗传算法调试技巧：快速定位和解决问题的五大秘诀

# 1. 遗传算法简介及其在MATLAB中的应用

在探索复杂的优化问题时，传统的确定性算法可能显得力不从心，特别是在面对非线性、不连续或者具有多个局部最优解的问题时。遗传算法，作为一种基于自然选择和遗传学原理的搜索算法，为解决这些问题提供了一种全新的视角。本章节将简要介绍遗传算法的基本概念，并探讨其在MATLAB这一强大的科学计算平台中的应用。

遗传算法的核心思想是模拟自然界的进化过程。它从一组随机生成的解（种群）开始，通过选择（Selection）、交叉（Crossover）和变异（Mutation）这三种机制迭代地进行优化，最终趋向于找到问题的最优解或近似最优解。

在MATLAB中，遗传算法得到了广泛的应用，这归功于MATLAB强大的矩阵操作能力和内置的遗传算法工具箱（如Global Optimization Toolbox）。通过这些工具箱，研究人员和工程师可以轻松实现遗传算法，并将其应用于各种优化问题，从工程设计到数据分析，再到机器学习模型参数的优化。在接下来的章节中，我们将深入探讨遗传算法的理论基础，MATLAB中的具体实现，以及如何在实际应用中调试和优化遗传算法。

# 2. MATLAB遗传算法的理论基础

### 2.1 遗传算法的基本概念

#### 2.1.1 遗传算法的起源和原理

遗传算法（Genetic Algorithms，GA）是一种模拟自然选择和遗传学机制的搜索启发式算法。它起源于20世纪70年代，由John Holland及其学生和同事们发展而来。GA受到生物进化论的启发，通过模拟自然选择的过程，算法迭代地选择优秀个体并产生新的群体，旨在找到问题的最优解或满意解。

在遗传算法中，潜在的解决方案被视为个体，它们组成一个群体，并在这个群体中通过选择、交叉（即杂交）和变异等操作进行演变。每一个个体都有一个由问题域决定的适应度值，这个值代表了该个体解决问题的能力。遗传算法通过模拟自然界的“适者生存”法则，保留适应度高的个体，淘汰适应度低的个体，以此推动群体向更好的方向发展。

遗传算法的关键点在于：
- **选择**：根据个体的适应度选择优良的个体参与繁殖。
- **交叉**：模仿生物遗传中的染色体交叉，交换父代个体的部分基因，产生新的子代。
- **变异**：随机改变个体基因中的某些部分，以增加种群的多样性，避免算法过早收敛于局部最优解。

遗传算法的原理是建立在这样的信念之上：自然界的生物进化过程能够解决复杂问题，因此通过模拟这一过程，我们可以在计算机上解决工程和科学问题。

#### 2.1.2 遗传算法的主要操作：选择、交叉和变异

在遗传算法中，选择、交叉和变异是三个基本且关键的操作，它们决定了算法的搜索能力和最终解的质量。

- **选择操作**：目的是从当前种群中选择出适应度高的个体，作为繁殖后代的父本。有多种选择策略，如轮盘赌选择、锦标赛选择等。轮盘赌选择模拟了“物竞天择”的过程，每个个体被选中的概率与其适应度成正比。而锦标赛选择则是随机选取几个个体，然后从中选择出最佳者参与繁殖。

- **交叉操作**：又称为杂交，是指将两个（或多个）个体的某些部分进行交换，从而生成新的个体。它模拟生物染色体交叉的自然现象，是遗传算法产生新解的主要途径。常用的交叉方法包括单点交叉、双点交叉、均匀交叉等。

- **变异操作**：变异过程是对个体的某些基因进行随机改变，以增加种群的多样性，防止算法陷入局部最优解。变异可以是单点变异、多点变异、插入变异等。变异概率通常较低，以确保遗传算法的稳定性和进化方向。

### 2.2 遗传算法的数学模型

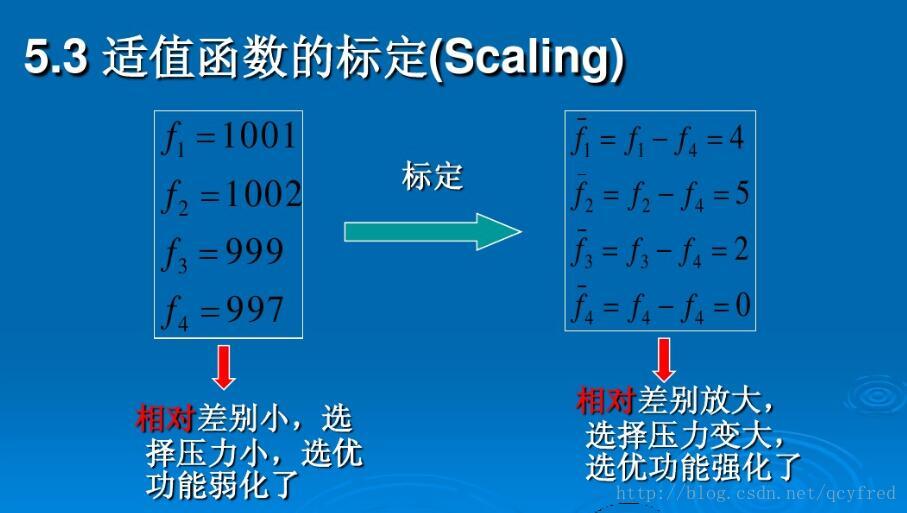
#### 2.2.1 适应度函数的设计

适应度函数是遗传算法中的核心概念之一，它用于评价个体对环境的适应能力，即解决方案的优劣。设计一个有效的适应度函数对于遗传算法的成功至关重要。适应度函数需要准确反映个体的质量，并能够指导搜索过程朝着最优解方向发展。

适应度函数通常依赖于所要解决的具体问题，其设计应遵循以下原则：
- **单调性**：适应度函数应与其代表的性能指标呈正比，即性能指标越高，适应度应越高。
- **简单性**：适应度函数的计算过程应尽量简单，避免复杂度高导致的运行时间过长。
- **鲁棒性**：适应度函数应能处理异常值，对各种情况下的个体适应度值有合理的反应。

举个例子，如果我们要在遗传算法中解决一个最小化问题，我们可能会选择性能指标的倒数作为适应度值，即适应度函数 `f(x) = 1 / (1 + J(x))`，其中 `J(x)` 是问题的性能指标函数，它反映了个体 `x` 的优劣。

#### 2.2.2 群体和基因型的表现形式

在遗传算法中，每一个个体通常用一串称为基因型的编码来表示。基因型可以是二进制串、实数串、符号串或其他任何一种能够合理表达问题域信息的编码形式。群体则由多个个体组成，形成一个搜索空间。

- **二进制编码**：这是遗传算法中最常用的一种编码方式。二进制编码将问题解映射为一串二进制数字，每个基因位（bit）可以为0或1。例如，在解决0-1背包问题时，一个基因位可以表示某个物品是否被选中。

- **实数编码**：对于一些参数优化问题，使用实数编码更为直观和方便。例如，基因型可以直接是一个实数向量，每个基因位对应一个优化参数的值。

- **符号编码**：当问题的解可以用一组符号表达时，符号编码是一种有效的方法。例如，在旅行商问题（TSP）中，基因型可以是城市序列。

编码方式的选择取决于具体问题的性质和搜索空间的特性。在设计遗传算法时，需要根据问题的特点选择合适的编码方式，以及相应的交叉和变异操作。

### 2.3 遗传算法的参数设置

#### 2.3.1 种群大小和交叉率的调节

种群大小和交叉率是影响遗传算法性能的两个关键参数。它们的设置对于算法搜索效率和解的质量起着至关重要的作用。

- **种群大小**：种群大小决定了每一代中个体的数量。种群太小，可能导致搜索空间覆盖不足，降低解的质量；而种群太大，则会增加计算资源的消耗，延长运行时间。通常需要通过实验调整种群大小，以达到最佳的搜索效果。

- **交叉率**：交叉率决定了一对个体进行交叉操作的概率。交叉率高意味着更多个体参与交叉，算法更有机会搜索到新的解空间，但也可能破坏优秀个体的结构。较低的交叉率可以保持优秀个体的基因结构，但可能会减缓算法的搜索进程。通常情况下，交叉率设定在0.6到0.9之间。

#### 2.3.2 变异率和选择机制的影响

变异率和选择机制同样是影响遗传算法性能的重要参数。

- **变异率**：变异率决定了种群中个体基因发生变异的概率。适当的变异率可以引入新的遗传多样性，避免算法早熟收敛。变异率太低，算法可能陷入局部最优；变异率太高，则可能导致算法行为过于随机。常见的变异率设置在0.001到0.01之间。

- **选择机制**：选择机制影响着遗传算法的选择压力。选择压力即算法保留优秀个体进入下一代的概率。过高的选择压力可能造成早熟收敛，而过低的选择压力则可能导致收敛速度过慢。常见的选择机制包括轮盘赌选择、锦标赛选择、精英策略等。

通过合理配置这些参数，遗传算法能够在保持搜索效率的同时，寻找到问题的优质解或者全局最优解。参数的调整往往需要结合问题的具体特性和多次试验来进行优化。

### 2.4 本章小结

本章深入探讨了遗传算法的理论基础，从遗传算法的基本概念出发，介绍了其起源和原理，以及关键操作：选择、交叉和变异。随后，我们对遗传算法的数学模型进行了详细分析，包括适应度函数的设计和群体及基因型的表现形式。

通过对种群大小、交叉率、变异率以及选择机制这些关键参数的讨论，我们认识到了它们对于遗传算法性能的影响。这些理论知识为我们深入理解和有效应用遗传算法提供了坚实的理论基础。

在第三章，我们将进一步探讨如何在MATLAB环境中调试和优化遗传算法，以确保算法在实际应用中能够达到最佳效果。

# 3. MATLAB遗传算法的调试技巧

在成功部署遗传算法前，充分的调试过程是不可或缺的。本章将详细介绍MATLAB环境下遗传算法调试的技巧和方法，帮助读者更快地定位问题、优化算法性能。

## 3.1 调试前的准备工作

### 3.1.1 确定调试目标和计划

调试的第一步是明确目标，制定合理的调试计划。目标通常包括发现和修复程序中的错误、确保算法按照预期工作、优化算法的性能指标等。计划则需要包括以下内容：

- **定义预期结果：** 每个测试用例的目标结果。
- **设计测试用例：** 包括各种边界情况、异常输入和可能的错误场景。
- **调试环境的构建：** 准备MATLAB环境和相关工具包。
- **数据准备：** 包括训练数据、测试数据的准备以及数据的预处理。

### 3.1.2 构建调试环境和测试用例

在MATLAB中构建调试环境需要考虑以下方面：

- **MATLAB版本：** 确保使用的MATLAB版本与算法开发环境一致。
- **工具箱安装：** 确认遗传算法工具箱是否安装。
- **辅助工具的准备：** 准