手写数字识别：探索不同的神经网络架构

# 1. 手写数字识别问题概述

## 1.1 手写数字识别的应用背景
手写数字识别是计算机视觉领域的一项基础而重要的任务，其应用广泛，从邮政编码识别到自动填写银行支票上的数字，再到现在流行的数字键盘应用。这一问题的解决不仅推动了计算机视觉技术的进步，也深入到了我们的日常生活。

## 1.2 手写数字识别的技术挑战
尽管手写数字识别看似简单，但其背后隐藏了诸多技术挑战。由于每个人的书写风格差异巨大，加上数字之间形状相似（如1和7，2和5），使得实现高准确率的手写数字识别充满挑战。这就需要运用到先进的机器学习和深度学习算法。

## 1.3 神经网络在手写数字识别中的作用
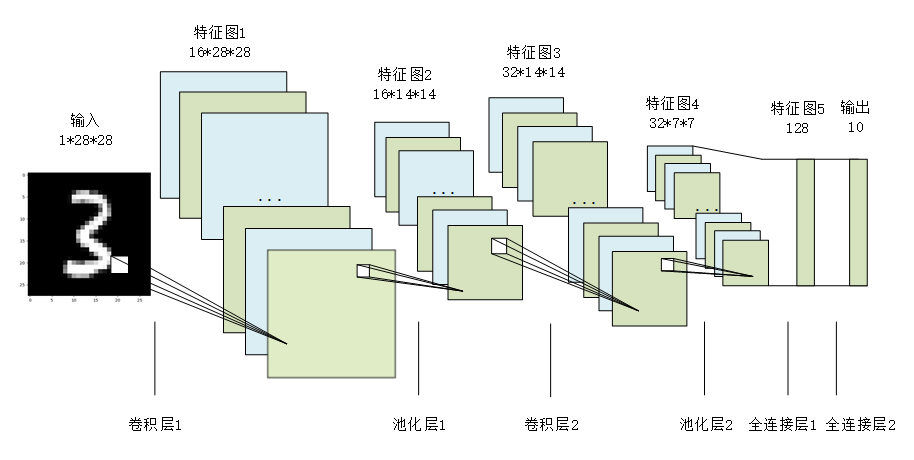
神经网络，尤其是深度学习的卷积神经网络（CNN），因其在图像处理方面的优异性能，已经成为解决手写数字识别问题的首选方法。CNN能自动从数据中学习到复杂的特征，无需人工设计，极大提高了识别准确率和效率。

# 2. 基础神经网络架构分析

### 2.1 神经网络基础理论

#### 2.1.1 神经网络的定义和组成

神经网络是一种受人脑启发的计算模型，它由大量的神经元或节点组成，这些神经元通过加权的连接相互连接。每个神经元通常会接收来自其他神经元的输入，进行加权求和后，通过一个非线性激活函数产生输出。神经网络的层级结构可以分为输入层、隐藏层（可能有多个）和输出层。

graph LR
A[输入层] -->|数据输入| B[隐藏层1]
B --> C[隐藏层2]
C -->|...| D[隐藏层n]
D --> E[输出层]

每个隐藏层可以包含多个神经元，而输出层的神经元数量取决于任务的输出类型，例如在手写数字识别中，输出层将有10个神经元，每个代表一个数字的类别（0-9）。

#### 2.1.2 前向传播和反向传播算法

前向传播是指输入数据在网络中逐层传递，最终在输出层产生结果的过程。具体来说，输入数据在每一层中会通过神经元的加权求和和激活函数，向后传递到下一层。

# 假设有一个单隐藏层的简单神经网络，其向前传播的代码可能如下所示：
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def forward_pass(X, weights_input_hidden, weights_hidden_output):
    hidden_layer_input = np.dot(X, weights_input_hidden)
    hidden_layer_output = sigmoid(hidden_layer_input)
    final_output = np.dot(hidden_layer_output, weights_hidden_output)
    prediction = sigmoid(final_output)
    return prediction

反向传播算法是一种用于训练神经网络的技术。它通过计算损失函数关于网络参数（权重和偏置）的梯度来工作。这些梯度由链式法则获得，并用于更新网络参数，以减少输出和实际标签之间的差异。

# 反向传播算法的梯度计算部分可能如下所示：
def sigmoid_derivative(x):
    return x * (1 - x)

def back_propagation(X, y, output, hidden_layer_output, weights_hidden_output, weights_input_hidden):
    error = y - output
    d_predicted_output = error * sigmoid_derivative(output)
    error_hidden_layer = d_predicted_output.dot(weights_hidden_output.T)
    d_hidden_layer = error_hidden_layer * sigmoid_derivative(hidden_layer_output)
    # 这里假设使用均方误差损失函数
    d_weights_hidden_output = hidden_layer_output.T.dot(d_predicted_output)
    d_weights_input_hidden = X.T.dot(d_hidden_layer)
    return d_weights_hidden_output, d_weights_input_hidden

### 2.2 卷积神经网络（CNN）基础

#### 2.2.1 卷积层的作用和结构

卷积层是卷积神经网络（CNN）的核心组成部分，主要负责图像特征的提取。在卷积层中，使用一组学习得到的过滤器（或称为卷积核）在输入图像上滑动，进行元素级别的乘法和求和操作，从而生成一系列的特征图（feature maps）。

# 一个简单的卷积操作的代码示例：
def convolve2d(image, kernel):
    # 以边缘填充图像
    pad_width = kernel.shape[0] // 2
    padded_image = np.pad(image, [(pad_width, pad_width), (pad_width, pad_width)], mode='constant', constant_values=0)
    # 进行卷积操作
    output = np.zeros_like(image)
    for i in range(image.shape[0]):
        for j in range(image.shape[1]):
            output[i, j] = np.sum(kernel * padded_image[i:i+kernel.shape[0], j:j+kernel.shape[1]])
    return output

#### 2.2.2 池化层及其重要性

池化层（Pooling Layer）通常紧随卷积层之后，用于降低特征图的空间维度，从而减少计算量和防止过拟合。池化操作一般有两种类型：最大池化（Max Pooling）和平均池化（Average Pooling）。

# 最大池化的示例代码：
def max_pooling(feature_map, pool_size=2):
    padded_feature_map = np.pad(feature_map, [(0, 0), (1, 1), (1, 1)], mode='constant', constant_values=0)
    feature_map_shape = feature_map.shape
    pooled_feature_map = np.zeros((feature_map_shape[0], feature_map_shape[1] // pool_size, feature_map_shape[2] // pool_size))

    for i in range(0, feature_map_shape[1], pool_size):
        for j in range(0, feature_map_shape[2], pool_size):
            pool_region = padded_feature_map[:, i:i+pool_size, j:j+pool_size]
            pooled_feature_map[:, i//pool_size, j//pool_size] = np.max(pool_region, axis=(1, 2))
    return pooled_feature_map

### 2.3 常见的全连接网络结构

#### 2.3.1 全连接层的工作原理

全连接层（Fully Connected Layer，FC Layer）在神经网络中位于最后，用来整合前面卷积层和池化层提取的特征，并进行最终的分类或者回归预测。在全连接层中，每个输入节点都与下一个层中的每个节点相连，所有连接都有相应的权重。

# 全连接层的代码示例：
def fully_connected(input, weights, bias):
    return np.dot(input, weights) + bias

#### 2.3.2 全连接层在手写数字识别中的应用

在手写数字识别的任务中，经过前面的卷积层和池化层提取到足够抽象的特征后，全连接层可以用来学习这些特征与数字类别之间的复杂非线性关系。一般会在网络的末端使用一个或多个全连接层来实现最终的分类。

# 实际应用中的全连接层可能如下所示：
input_size = 7*7*64  # 假设最后一层卷积层输出大小为 64 个 7x7 的特征图
hidden_size = 1024  # 隐藏层节点数

weights = np.random.randn(input_size, hidden_size)  # 随机初始化权重
bias = np.zeros((1, hidden_size))  # 初始化偏置

# 假设 feature_map 是经过卷积和池化层处理后的特征图
hidden_layer_output = fully_connected(feature_map.reshape((-1, input_size)), weights, bias)

全连接层在将输入的特征图展平后进行线性变换，然后通常会应用一个激活函数，比如ReLU，以增加网络的非线性能力和提高模型的泛化能力。

# 3. 深度学习框架与工具

## 3.1 选择合适的深度学习框架

### 3.1.1 TensorFlow基础

TensorFlow是由Google开发的开源机器学习库，它提供了一套全面的API，用以构建和训练机器学习模型。它广泛应用于图像识别、自然语言处理、时间序列预测等领域。TensorFlow的核心是计算图，它是一种用于定义和执行数学运算的框架。

#### 计算图的构建

在TensorFlow中，计算图是通过定义一系列的操作（Operations）和张量（Tensors）来构建的。操作表示计算过程，张量代表数据。一个操作可以接受零个或多个张量作为输入，然后输出一个或多个张量。

import tensorflow as tf

# 创建常量张量
a = tf.constant(2.0)
b = tf.constant(3.0)

# 定义操作，将两个张量相加
result = tf.add(a, b)

# 创建会话并运行计算图
with tf.Session() as sess:
    print(sess.run(result))  # 输出: 5.0

#### 张量的命名作用域

张量命名作用域（tf.name_scope）是一个强大的工具，可以帮助开发者组织和可视化复杂的计算图。它为作用域内的操作和张量提供了一个前缀，使得在TensorBoard这样的可视化工具中可以更清晰地区分它们。

import tensorflow as tf

# 使用命名作用域组织计算图
with tf.name_scope('addition') as scope:
    a = tf.constant(2.0, name='a')
    b = tf.constant(3.0, name='b')
    result = tf.add(a, b, name='addition_result')

print("操作 'addition_result' 在图中的完整名称是: ", result.name)

### 3.1.2 PyTorch的动态计算图

PyTorch是一种用于计算机视觉和自然语言处理任务的流行深度学习框架。与TensorFlow不同，PyTorch使用动态计算图，即图是在运行时构建的，这使得它在研究和调试时更加灵活。

#### 动态计算图的优势

动态计算图（也称为定义即运行模式）的一个主要优势是能够更好地利用Python的控制流。用户可以在运行时根据条件改变网络结构，这对于循环神经网络和复杂的神经网络结构特别有用。

import torch

# PyTorch使用动态计算图
a = torch.tensor(2.0, requires_grad=True)
b = torch.tensor(3.0, requires_grad=True)

# 定义一个操作
result = a + b

# 反向传播
result.backward()

print("a 的梯度是: ", a.grad)

#### 张量和操作的自动求导

PyTorch通过autograd包自动求解梯度，这对于深度学习模型的训练至关重要。当创建一个张量时，通过设置`requires_grad=True`，PyTorch会记录所有随后对该张量的操作，并在调用`.backward()`时计算梯度。

import torch

# 创建一个张量
x = torch.ones(2, 2, requir