LAPACK矩阵乘法算法优化：从基础到高效计算

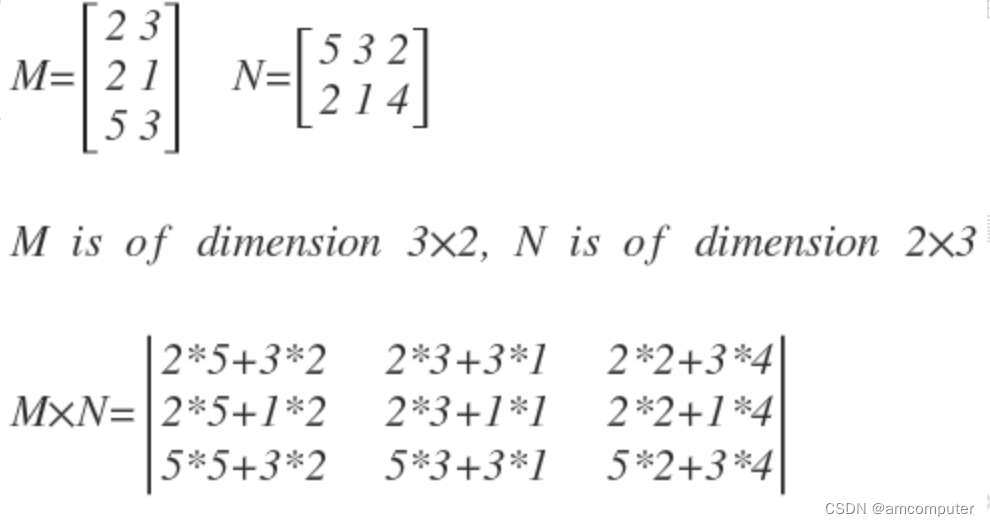
# 1. LAPACK矩阵乘法的基本原理

LAPACK（线性代数包）是一个用于数值线性代数的高性能计算库。它提供了广泛的例程，用于执行各种矩阵运算，包括矩阵乘法。

矩阵乘法是线性代数中的基本操作，用于计算两个矩阵的乘积。在LAPACK中，矩阵乘法由 `DGEMM` 例程执行，该例程采用以下形式：

void dgemm(char transa, char transb, int m, int n, int k, double alpha, const double *A, int lda, const double *B, int ldb, double beta, double *C, int ldc);

其中：

* `transa` 和 `transb` 指定是否对 `A` 和 `B` 进行转置。
* `m`, `n`, `k` 指定矩阵的尺寸。
* `alpha` 和 `beta` 是标量因子。
* `A`, `B`, `C` 是输入和输出矩阵。
* `lda`, `ldb`, `ldc` 是矩阵的领先维度。

# 2. LAPACK矩阵乘法优化技术

### 2.1 算法选择和优化

#### 2.1.1 传统算法与优化算法的对比

传统矩阵乘法算法，如朴素算法，具有时间复杂度 O(n^3)。对于大型矩阵，这种算法计算量巨大，效率低下。优化算法，如 Strassen 算法和 Winograd 算法，通过分解矩阵并使用递归策略，将时间复杂度降低为 O(n^2.8) 或 O(n^2.376)，大大提高了计算效率。

#### 2.1.2 不同硬件平台的算法选择

不同的硬件平台对算法的性能有显著影响。对于 CPU 平台，Strassen 算法和 Winograd 算法通常表现出色。对于 GPU 平台，由于其并行处理能力，基于分块的算法，如 Cannon 算法和 Summation 算法，可以充分利用 GPU 的优势。

### 2.2 并行化优化

#### 2.2.1 多线程并行化

多线程并行化通过将矩阵乘法任务分配给多个线程并行执行，可以有效提高计算速度。OpenMP 和 TBB 等并行编程库提供了方便的接口，使开发者可以轻松实现多线程并行化。

#### 2.2.2 分布式并行化

分布式并行化将矩阵乘法任务分配给分布在不同节点上的多个进程并行执行。MPI 等消息传递接口库用于进程间的通信和数据交换。分布式并行化适用于处理超大规模矩阵，可以充分利用集群计算资源。

### 2.3 内存优化

#### 2.3.1 缓存优化

缓存优化通过将频繁访问的数据存储在高速缓存中，减少内存访问延迟，提高计算效率。LAPACK 提供了 `LAPACKE_set_blocksize` 函数，允许用户指定矩阵块的大小，以优化缓存利用率。

#### 2.3.2 数据结构优化

选择合适的矩阵数据结构可以显著影响内存访问效率。LAPACK 提供了多种矩阵数据结构，如密集矩阵、稀疏矩阵和对称矩阵。根据矩阵的特征选择合适的结构，可以减少内存占用和提高计算速度。

import numpy as np

# 创建密集矩阵