【LAPACK矩阵计算秘籍】：揭秘矩阵计算库的强大功能

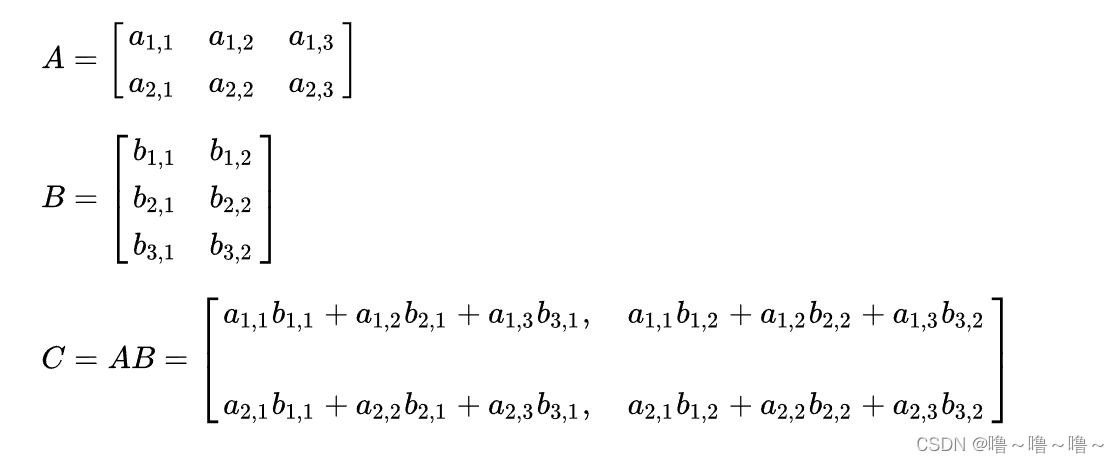
# 1. LAPACK矩阵计算概述**

LAPACK（线性代数包）是一个广泛使用的科学计算库，专门用于矩阵计算。它提供了一系列高效且稳定的例程，用于解决各种矩阵相关问题，包括线性方程组求解、矩阵分解和特征值计算。

LAPACK库的优势在于其高性能和跨平台兼容性。它利用了优化算法和并行计算技术，以在各种硬件架构上实现最佳性能。此外，LAPACK库是开源的，并提供详细的文档和支持资源，使其易于集成到各种应用程序中。

# 2. LAPACK矩阵计算基础

### 2.1 LAPACK库的基本概念

#### 2.1.1 矩阵存储格式

LAPACK库使用两种主要的矩阵存储格式：

- **行主序存储：**元素按行存储，即矩阵的第i行第j列元素存储在位置a(i, j)。
- **列主序存储：**元素按列存储，即矩阵的第i行第j列元素存储在位置a(j, i)。

LAPACK库默认使用行主序存储，但也可以通过指定FORTRAN存储顺序参数来使用列主序存储。

#### 2.1.2 基本矩阵运算

LAPACK库提供了广泛的基本矩阵运算，包括：

- 加法和减法：`dgemm`、`zgemm`
- 乘法：`dgemm`、`zgemm`
- 转置：`dtranspose`、`ztranspose`
- 缩放：`dscal`、`zscal`

### 2.2 LAPACK矩阵分解算法

LAPACK库提供了多种矩阵分解算法，包括：

#### 2.2.1 LU分解

LU分解将一个矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积：

A = LU

LAPACK库中使用`dgetrf`和`zgetrf`函数进行LU分解。

**参数说明：**

- `A`：输入/输出矩阵，分解后存储LU分解结果。
- `lda`：A的领先维度。
- `ipiv`：一个整数数组，存储LU分解中的置换信息。

**代码逻辑分析：**

`dgetrf`函数使用高斯消去法逐行分解矩阵。它通过交换行和列来保持矩阵的非奇异性，并使用置换数组`ipiv`记录这些交换。

#### 2.2.2 QR分解

QR分解将一个矩阵分解为一个正交矩阵和一个上三角矩阵的乘积：

A = QR

LAPACK库中使用`dgeqrf`和`zgeqrf`函数进行QR分解。

**参数说明：**

- `A`：输入/输出矩阵，分解后存储QR分解结果。
- `lda`：A的领先维度。
- `tau`：一个双精度数组，存储QR分解中的反射信息。

**代码逻辑分析：**

`dgeqrf`函数使用Householder变换逐列分解矩阵。它通过对矩阵的每一列进行一系列反射变换来构造正交矩阵Q和上三角矩阵R。

#### 2.2.3 奇异值分解

奇异值分解将一个矩阵分解为三个矩阵的乘积：

A = UΣV^T

其中U和V是正交矩阵，Σ是对角矩阵，包含矩阵的奇异值。

LAPACK库中使用`dgesvd`和`zgesvd`函数进行奇异值分解。

**参数说明：**

- `A`：输入/输出矩阵，分解后存储奇异值分解结果。
- `lda`：A的领先维度。
- `s`：一个双精度数组，存储矩阵的奇异值。
- `u`：一个双精度数组，存储正交矩阵U。
- `vt`：一个双精度数组，存储正交矩阵V的转置。

**代码逻辑分析：**

`dgesvd`函数使用QR分解和Jacobi方法进行奇异值分解。它首先将矩阵分解为QR分解，然后使用Jacobi方法对上三角矩阵进行对角化，得到奇异值和正交矩阵。

# 3. LAPACK矩阵计算实践

### 3.1 线性方程组求解

#### 3.1.1 直接求解法

直接求解法是通过一系列矩阵运算将线性方程组化为三角形方程组，再通过向前或向后替换法求解方程组。LAPACK库提供了多种直接求解法，包括：

- **LU分解法**：将系数矩阵分解为下三角矩阵和上三角矩阵的乘积，然后分别求解三角形方程组。
- **QR分解法**：将系数矩阵分解为正交矩阵和上三角矩阵的乘积，然后求解上三角形方程组。

import numpy as np
from scipy.linalg import lu, solve

# 系数矩阵
A = np.array([[2, 1, 1], [4, 3, 2], [8, 7, 4]])

# 右端项向量
b = np.array([1, 2, 3])

# LU分解
P, L, U = lu(A)

# 前向替换求解Ly=Pb
y = solve(L, P.T @ b)

# 后向替换求解Ux=y
x = solve(U, y)

print(x)  # 输出求解结果

**代码逻辑分析：**

1. `lu()`函数进行LU分解，返回置换矩阵`P`、下三角矩阵`L`和上三角矩阵`U`。
2. `solve()`函数用于求解三角形方程组，`P.T @ b`将右端项向量经过置换矩阵变换，`L`和`U`分别用于求解`Ly=Pb`和`Ux=y`。
3. 最终`x`为求解的线性方程组的解向量。

#### 3.1.2 迭代求解法

迭代求解法通过不断迭代的方式逼近线性方程组的解。LAPACK库提供了多种迭代求解法，包括：

- **Jacobi迭代法**：每次迭代更新一个未知量的值，直到满足收敛条件。
- **Gauss-Seidel迭代法**：每次迭代更新所有未知量的值，直到满足收敛条件。

import numpy as np
from scipy.linalg import inv

# 系数矩阵
A = np.array([[2, 1, 1], [4, 3, 2], [8, 7, 4]])

# 右端项向量
b = np.array([1, 2, 3])

# 迭代次数
max_iter = 100

# 初始解向量
x = np.zeros(3)

# Jacobi迭代
for i in range(max_iter):
    for j in range(3):
        x[j] = (b[j] - np.dot(A[j, :j], x[:j]) - np.dot(A[j, j+1:], x[j+1:])) / A[j, j]

# Gauss-Seidel迭代
for i in range(max_iter):
    for j in range(3):
        x[j] = (b[j] - np.dot(A[j, :j], x[:j]) - np.dot(A[j, j+1:], x[j+1:])) / A[j, j]

print(x)  # 输出求解结果

**代码逻辑分析：**

1. `inv()`函数求解矩阵的逆矩阵，用于验证迭代求解结果。
2. Jacobi迭代和Gauss-Seidel迭代的迭代过程类似，区别在于Gauss-Seidel迭代在更新未知量时使用了最新迭代的值。
3. 最终`x`为求解的线性方程组的解向量。

# 4.1 高性能矩阵计算

### 4.1.1 并行计算技术

随着矩阵计算规模的不断扩大，单核计算的性能瓶颈日益凸显。并行计算技术通过将计算任务分配给多个处理器或计算节点，可以显著提高矩阵计算的性能。

**OpenMP**

OpenMP是一种基于共享内存的并行编程模型，允许程序员使用指令将代码段标记为并行执行。OpenMP支持多线程编程，可以在一台计算机上同时使用多个CPU核心。

**MPI**

MPI（消息传递接口）是一种基于分布式内存的并行编程模型，允许程序员在不同的计算机之间交换消息和数据。MPI支持多进程编程，可以在一台或多台计算机上同时使用多个进程。

**代码块：OpenMP并行矩阵乘法**

#include <omp.h>

void matrix_multiply(double *A, double *B, double *C, int n) {
  int i, j, k;

  #pragma omp parallel for private(j, k)
  for (i = 0; i < n; i++) {
    for (j = 0; j < n; j++) {
      C[i * n + j] = 0;
      for (k = 0; k < n; k++) {
        C[i * n + j] += A[i * n + k] * B[k * n + j];
      }
    }
  }
}

**逻辑分析：**

这段代码使用OpenMP并行化矩阵乘法计算。`#pragma omp parallel for`指令将外部循环（`i`循环）标记为并行执行，这意味着每个线程将负责计算矩阵C中的一行。内部循环（`j`和`k`循环）是串行的，因为它们需要访问共享数据（矩阵A和B）。

### 4.1.2 优化算法和数据结构

除了并行计算技术外，优化算法和数据结构也是提高矩阵计算性能的关键因素。

**分块算法**

分块算法将矩阵划分为较小的块，然后并行计算每个块。这可以减少共享数据访问的争用，从而提高并行效率。

**稀疏矩阵**

稀疏矩阵是一种存储格式，只存储矩阵中非零元素。稀疏矩阵可以显著减少内存占用和计算量，尤其是在矩阵中非零元素较少的情况下。

**代码块：稀疏矩阵存储格式**

import scipy.sparse as sp

A = sp.sparse.csr_matrix([[1, 2, 0], [0, 3, 4], [5, 0, 6]])

print(A)

**逻辑分析：**

这段代码使用SciPy库创建了一个稀疏矩阵`A`。`csr_matrix`表示压缩稀疏行格式，其中矩阵的非零元素存储在三个数组中：`data`（非零元素值）、`indices`（非零元素在行中的索引）和`indptr`（每行的非零元素开始索引）。

# 5.1 LAPACK库的安装和使用

### 5.1.1 库的获取和编译

**获取LAPACK库：**

- 从官方网站（https://www.netlib.org/lapack/）下载LAPACK库。
- 或者使用包管理器，如：
- Linux：`sudo apt-get install liblapack-dev`
- macOS：`brew install lapack`

**编译LAPACK库：**

- 解压下载的LAPACK包。
- 进入解压后的目录，执行以下命令：

    make
    make install

### 5.1.2 库函数的使用

**链接LAPACK库：**

在编译使用LAPACK库的程序时，需要链接LAPACK库。例如，使用GCC编译器：

gcc -o my_program my_program.c -llapack

**使用LAPACK函数：**

LAPACK库提供了大量的函数，用于执行各种矩阵计算。以下是一些常用的函数：

- **求解线性方程组：**
- `dgesv`：使用高斯消去法求解双精度实数线性方程组。
- **计算矩阵特征值和特征向量：**
- `dgeev`：计算双精度实数矩阵的特征值和特征向量。
- **求矩阵逆和行列式：**
- `dgetrf`：计算双精度实数矩阵的LU分解。
- `dgetri`：使用LU分解求矩阵逆。
- `ddet`：计算双精度实数矩阵的行列式。