MATLAB标准差与假设检验：数据分析的关键步骤

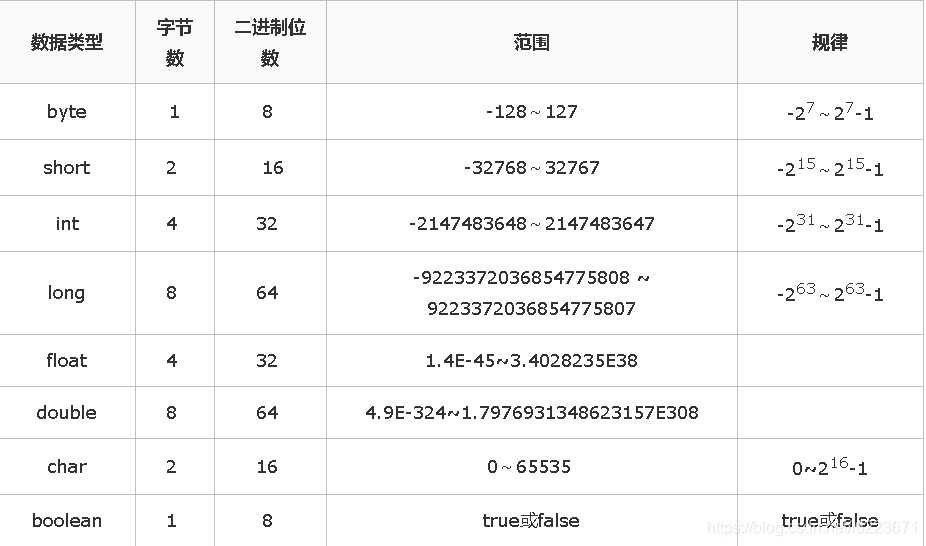
# 1. MATLAB中的标准差**

标准差是衡量数据集离散程度的重要指标。在MATLAB中，可以使用`std`函数计算标准差。该函数接受一个向量或矩阵作为输入，并返回一个包含每个列的标准差的向量。

% 计算一个向量的标准差
data = [1, 3, 5, 7, 9];
std_dev = std(data);

% 计算一个矩阵的标准差
data = [1, 3, 5; 2, 4, 6];
std_dev = std(data);

标准差可以帮助我们了解数据的分布情况。较小的标准差表示数据更集中在平均值周围，而较大的标准差表示数据更分散。

# 2. 假设检验的基础

**2.1 统计假设检验的概念和类型**

统计假设检验是一种统计推断方法，用于评估一个关于总体参数的假设是否成立。它涉及以下步骤：

* **提出假设：**提出关于总体参数的假设（称为原假设和备择假设）。
* **收集数据：**从总体中收集样本数据。
* **计算检验统计量：**使用样本数据计算一个检验统计量，该统计量衡量样本与假设之间的差异程度。
* **确定临界值：**根据假设和显著性水平确定一个临界值。
* **比较检验统计量和临界值：**如果检验统计量超过临界值，则拒绝原假设；否则，接受原假设。

假设检验的类型包括：

* **单样本检验：**用于比较样本均值或方差与已知值。
* **双样本检验：**用于比较两个独立样本的均值或方差。
* **方差分析（ANOVA）：**用于比较多个样本的均值。

**2.2 假设检验的步骤和方法**

假设检验的步骤如下：

1. **明确研究问题：**确定要检验的假设。
2. **选择检验方法：**根据研究问题和样本特征选择适当的假设检验方法。
3. **设定显著性水平：**确定拒绝原假设所需的概率阈值。
4. **收集数据：**从总体中收集代表性样本。
5. **计算检验统计量：**使用样本数据计算检验统计量。
6. **确定临界值：**根据假设和显著性水平确定临界值。
7. **比较检验统计量和临界值：**如果检验统计量超过临界值，则拒绝原假设；否则，接受原假设。
8. **解释结果：**根据检验结果做出结论，并考虑其对研究问题的意义。

常用的假设检验方法包括：

* **t检验：**用于比较样本均值。
* **方差分析（ANOVA）：**用于比较样本方差。
* **卡方检验：**用于检验分类数据分布的差异。
* **非参数检验：**用于分析非正态分布或序数数据。

# 3. 使用MATLAB进行假设检验

### 3.1 单样本t检验

#### 3.1.1 t检验的原理和假设

单样本t检验是一种用于检验单个样本均值是否与假设均值相等的统计检验。其原理是基于中心极限定理，即当样本量足够大时，样本均值近似服从正态分布。

假设检验的假设如下：

- **原假设（H0）：** 样本均值等于假设均值（μ0）
- **备择假设（H1）：** 样本均值不等于假设均值（μ0）

#### 3.1.2 在MATLAB中进行单样本t检验

MATLAB中使用`ttest`函数进行单样本t检验。该函数的语法如下：

[h,p,ci,stats] = ttest(x,mu0)

其中：

- `x`：样本数据
- `mu0`：假设均值
- `h`：假设检验结果（0表示不拒绝原假设，1表示拒绝原假设）
- `p`：p值
- `ci`：置信区间
- `stats`：统计信息

**示例：**

假设我们有一个样本数据，其均值为100，标准差为10。我们想要检验该样本均值是否与假