K折交叉验证在回归分析中的应用：模型评估与预测精度提升，优化模型预测效果

# 1. 回归分析简介**

回归分析是一种统计建模技术，用于预测连续型因变量（目标变量）与一个或多个自变量（预测变量）之间的关系。它旨在建立一个数学模型，描述因变量如何随自变量的变化而变化。回归模型可以用于预测未来值、识别变量之间的关系以及评估变量对因变量的影响。

# 2. K折交叉验证理论

### 2.1 K折交叉验证的原理

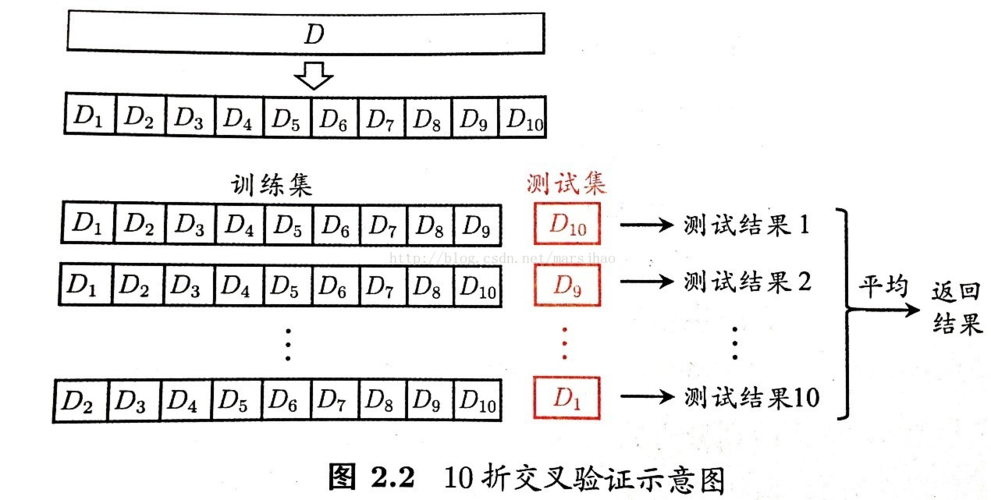
K折交叉验证是一种模型评估技术，它将数据集划分为K个大小相等的子集（折），然后使用K-1个折作为训练集，剩余的1个折作为测试集。该过程重复K次，每次使用不同的折作为测试集。

交叉验证背后的原理是，它可以提供模型在不同数据集上的性能估计。通过多次训练和测试模型，我们可以减少数据集划分对评估结果的影响，并获得更可靠的性能度量。

### 2.2 K折交叉验证的优点和缺点

**优点：**

* **减少过拟合：**交叉验证有助于防止模型过拟合训练集，因为它在不同的数据集上评估模型。
* **提高模型泛化能力：**通过在多个数据集上评估模型，交叉验证可以提供模型泛化到新数据的性能估计。
* **参数优化：**交叉验证可用于优化模型参数，例如正则化参数或超参数。
* **模型选择：**交叉验证可以帮助选择在不同数据集上表现最佳的模型。

**缺点：**

* **计算成本高：**交叉验证需要多次训练和测试模型，这可能会在大型数据集上变得计算成本高。
* **方差高：**交叉验证结果可能因数据集的划分方式而异，这可能会导致结果的方差较高。
* **可能存在偏差：**如果数据集不平衡或存在异常值，交叉验证结果可能会出现偏差。

### 代码示例

以下代码示例演示了如何使用Scikit-Learn库执行5折交叉验证：

from sklearn.model_selection import KFold

# 假设我们有一个训练数据集X和目标变量y
X = ...
y = ...

# 创建一个5折交叉验证对象
kf = KFold(n_splits=5, shuffle=True, random_state=42)

# 训练和评估模型
for train_index, test_index in kf.split(X, y):
    # 使用训练集训练模型
    model.fit(X[train_index], y[train_index])

    # 使用测试集评估模型
    score = model.score(X[test_index], y[test_index])

    # 记录分数
    scores.append(score)

# 计算平均分数
avg_score = np.mean(scores)

**代码逻辑分析：**

* `KFold`对象将数据集划分为5个大小相等的折。
* `shuffle=True`参数确保在划分折之前对数据进行随机洗牌。
* `random_state`参数设置随机种子，以确保每次运行代码时结果的可重复性。
* 循环通过交叉验证折，每次使用不同的折作为测试集。
* 在每个折上，模型在训练集上训练并使用测试集进行评估。
* 模型的得分（例如准确度或均方误差）被记录下来。
* 最后，计算所有折的平均得分，作为模型在数据集上的总体性能度量。

### 参数说明

* `n_splits`：交叉验证的折数。
* `shuffle`：是否在划分折之前对数据进行随机洗牌。
* `random_state`：随机种子的值。

# 3. K折交叉验证在回归分析中的实践

### 3.1 K折交叉验证的步骤

K折交叉验证的步骤如下：

1. **将数据集划分为K个大小相等的子集（折）：**将原始数据集随机划分为K个大小相等的子集，称为折。
2. **训练K个模型：**对于每个折，使用K-1个折作为训练集，剩余的1个折作为测试集。训练K个回归模型，每个模型使用不同的训练集。
3. **计算每个模型的性能：**使用测试集评估每个模型的性能，计算其均方根误差（RMSE）或其他评估指标。
4. **计算K个模型的平均性能：**将K个模型的性能指标取平均，得到K折交叉验证的最终性能指标。

### 3.2 K折交叉验证的评估指标

K折交叉验证的评估指标与回归分析中常用的评估指标相同，包括：

- **均方根误差（RMSE）：**衡量预测值与实际值之间的平均偏差。
- **平均绝对误差（MAE）：**衡量预测值与实际值之间的平均绝对偏差。
- **决定系数（R²）：**衡量模型预测值的方差与实际值方差之间的比例。

### 代码示例

以下 Python 代码演示了使用 scikit-learn 库执行 5 折交叉验证的步骤：

import numpy as np
from sklearn.model