Java排序算法空间优化：巧用空间优化技巧，提升算法效率，应对内存限制

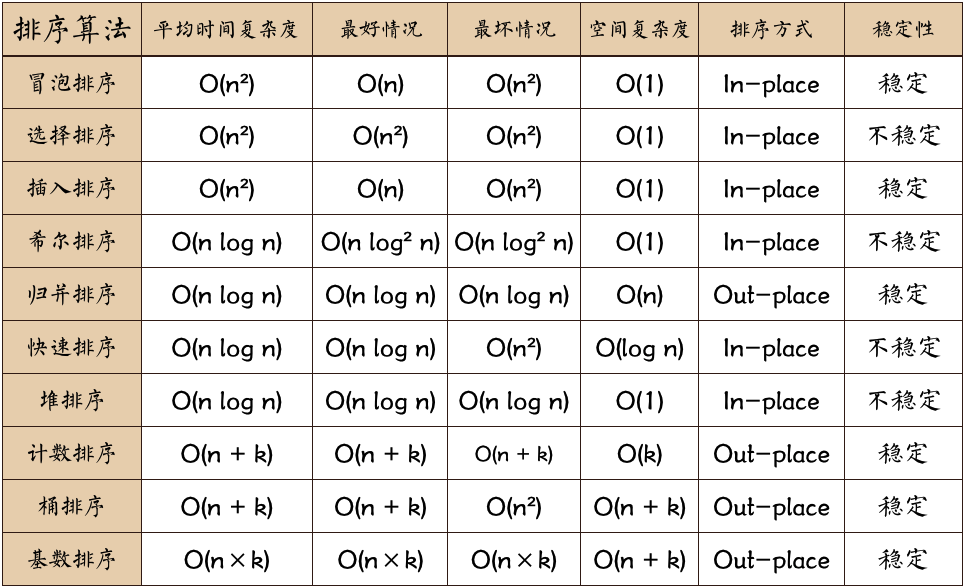
# 1. 排序算法简介

排序算法是计算机科学中基本且重要的算法，用于将一组元素按特定顺序排列。根据比较和交换元素的策略，排序算法可分为以下几类：

* **交换排序：**通过交换相邻元素来排序，如冒泡排序和快速排序。
* **插入排序：**将元素逐个插入到已排序的序列中，如直接插入排序和希尔排序。
* **选择排序：**通过找到最小（或最大）元素并将其移动到序列开头来排序，如简单选择排序和堆排序。
* **归并排序：**将序列递归地分成较小的子序列，对子序列进行排序，然后合并子序列。
* **快速排序：**选择一个枢纽元素，将序列分成小于和大于枢纽元素的两个子序列，然后递归地对子序列进行排序。

# 2. 空间优化技巧

排序算法通常需要额外的空间来存储临时数据，这可能会成为一个瓶颈，尤其是当处理海量数据时。为了解决这个问题，研究人员提出了各种空间优化技术，可以显著减少排序算法的内存占用。

### 2.1 计数排序

**原理：**

计数排序是一种非比较排序算法，它适用于数据范围有限且分布均匀的情况。该算法通过创建数据元素计数的数组来工作，然后利用计数数组来计算每个元素的最终位置。

**算法步骤：**

1. 确定数据元素的最大值和最小值。
2. 创建一个大小为最大值减去最小值加一的计数数组。
3. 遍历输入数组，将每个元素的计数增加 1。
4. 遍历计数数组，将每个元素的计数累加，得到每个元素的最终位置。
5. 遍历输入数组，根据最终位置将元素插入到输出数组中。

**代码实现：**

public static void countingSort(int[] arr) {
    int maxValue = Integer.MIN_VALUE;
    int minValue = Integer.MAX_VALUE;
    for (int num : arr) {
        if (num > maxValue) maxValue = num;
        if (num < minValue) minValue = num;
    }

    int[] countArray = new int[maxValue - minValue + 1];
    for (int num : arr) countArray[num - minValue]++;

    int[] outputArray = new int[arr.length];
    int index = 0;
    for (int i = 0; i < countArray.length; i++) {
        while (countArray[i] > 0) {
            outputArray[index++] = i + minValue;
            countArray[i]--;
        }
    }

    System.arraycopy(outputArray, 0, arr, 0, arr.length);
}

**逻辑分析：**

* `maxValue` 和 `minValue` 变量用于确定数据元素的最大值和最小值，从而确定计数数组的大小。
* 遍历输入数组，将每个元素的计数增加 1，存储在计数数组中。
* 遍历计数数组，将每个元素的计数累加，得到每个元素的最终位置。
* 遍历输入数组，根据最终位置将元素插入到输出数组中。

### 2.2 基数排序

**原理：**

基数排序是一种非比较排序算法，它适用于数据元素具有多个关键字的情况。该算法通过逐个关键字对数据元素进行排序，从最低有效位到最高有效位。

**算法步骤：**

1. 确定数据元素的最大值。
2. 创建一个大小为最大值加一的计数数组。
3. 遍历输入数组，将每个元素的最低有效位作为索引，将元素插入到计数数组中。
4. 遍历计数数组，将元素按顺序插入到输出数组中。
5. 重复步骤 3 和 4，对每个关键字进行排序。

**代码实现：**

public static void radixSort(int[] arr, int radix) {
    int maxValue = Integer.MIN_VALUE;
    for (int num : arr) if (num > maxValue) maxValue = num;

    int numDigits = (int) Math.log10(maxValue) + 1;
    for (int exp = 1; exp <= numDigits; exp++) {
        int[] countArray = new int[radix];
        int[] outputArray = new int[arr.length];

        for (int num : arr) countArray[num / exp % radix]++;

        for (int i = 1; i < radix; i++) countArray[i] += cou