【Java排序算法入门指南】：掌握排序算法基础，轻松理解算法原理

# 1. 排序算法概述**

排序算法是计算机科学中用于对数据集合进行排序的算法。排序算法根据其工作原理和复杂度可以分为不同的类型。本篇文章将介绍排序算法的基本概念、常见的排序算法及其应用。

排序算法的目的是将数据集合中的元素按特定顺序排列，例如升序或降序。排序算法的效率由其时间复杂度和空间复杂度决定。时间复杂度衡量算法执行所需的时间，而空间复杂度衡量算法执行所需的内存空间。

# 2. 基础排序算法

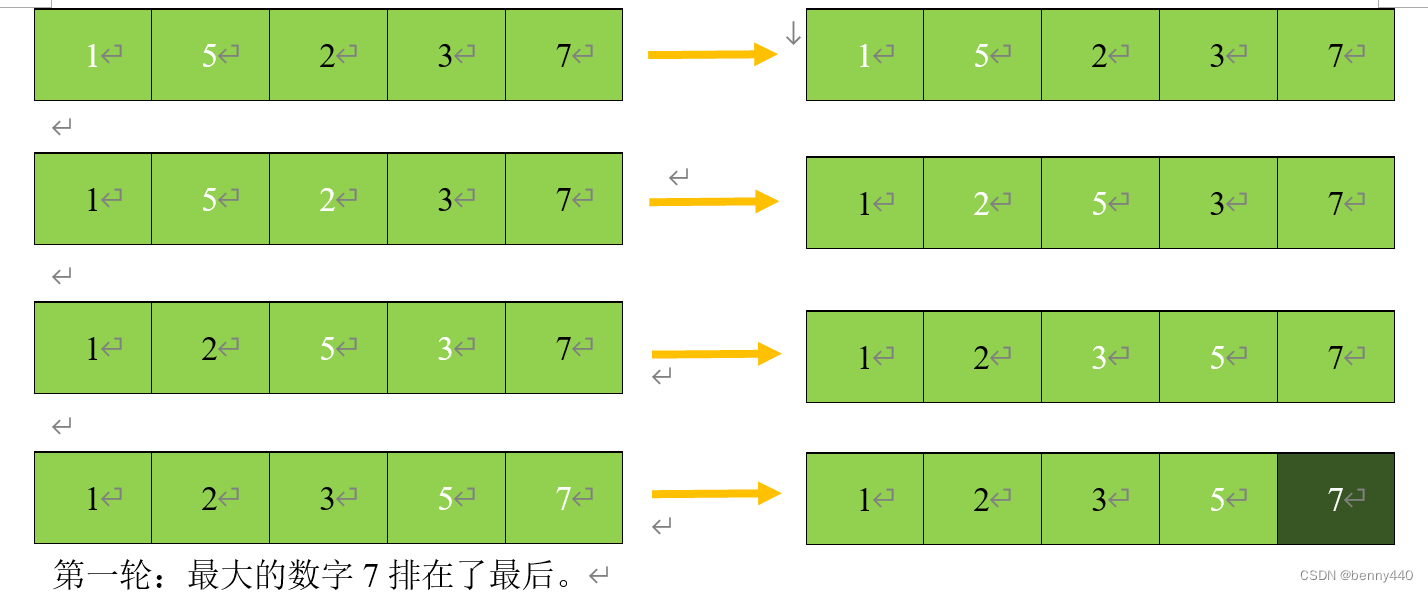
### 2.1 冒泡排序

#### 2.1.1 算法原理

冒泡排序是一种简单直观的排序算法。它的基本思想是：将相邻的两个元素进行比较，如果顺序错误，则交换它们。重复这一过程，直到没有元素需要交换为止。

**伪代码：**

for i = 0 to n - 1
    for j = 0 to n - i - 1
        if arr[j] > arr[j + 1]
            swap(arr[j], arr[j + 1])

#### 2.1.2 复杂度分析

* **时间复杂度：**

最坏情况：O(n^2)
最好情况：O(n)

最坏情况发生在数组完全逆序的情况下，需要进行 n*(n-1)/2 次比较和交换。最好情况发生在数组已经有序的情况下，只需要进行 n-1 次比较。

* **空间复杂度：** O(1)

冒泡排序不需要额外的空间，因此空间复杂度为常数。

### 2.2 选择排序

#### 2.2.1 算法原理

选择排序是一种不稳定的排序算法。它的基本思想是：在未排序的数组中找到最小（或最大）的元素，将其与第一个元素交换，然后重复这一过程，直到整个数组有序。

**伪代码：**

for i = 0 to n - 1
    min_idx = i
    for j = i + 1 to n - 1
        if arr[j] < arr[min_idx]
            min_idx = j
    swap(arr[i], arr[min_idx])

#### 2.2.2 复杂度分析

* **时间复杂度：** O(n^2)

选择排序需要进行 n*(n-1)/2 次比较和交换，因此时间复杂度为 O(n^2)。

* **空间复杂度：** O(1)

选择排序不需要额外的空间，因此空间复杂度为常数。

### 2.3 插入排序

#### 2.3.1 算法原理

插入排序是一种稳定的排序算法。它的基本思想是：将一个元素插入到已经有序的子数组中，使整个数组有序。

**伪代码：**

for i = 1 to n - 1
    key = arr[i]
    j = i - 1
    while j >= 0 and arr[j] > key
        arr[j + 1] = arr[j]
        j = j - 1
    arr[j + 1] = key

#### 2.3.2 复杂度分析

* **时间复杂度：**

最坏情况：O(n^2)
最好情况：O(n)

最坏情况发生在数组完全逆序的情况下，需要进行 n*(n-1)/2 次比较和移动。最好情况发生在数组已经有序的情况下，只需要进行 n-1 次比较。

* **空间复杂度：** O(1)

插入排序不需要额外的空间，因此空间复杂度为常数。

# 3.1 快速排序

#### 3.1.1 算法原理

快速排序是一种分治排序算法，其基本思想是：

1. **选取一个基准元素：**从数组中选取一个元素作为基准元素。
2. **分区：**将数组分成两部分：比基准元素小的元素放在基准元素的左边，比基准元素大的元素放在基准元素的右边。
3. **递归：**对两个分区分别进行快速排序。

#### 3.1.2 复杂度分析

快速排序的时间复杂度为：

* 最佳情况：O(n log n)，当数组是有序或接近有序时。
* 平均情况：O(n log n)，当数组是随机分布时。
* 最差情况：O(n^2)，当数组是逆序或接近逆序时。

#### 代码示例

def quick_sort(array):
    """
    快速排序算法

    参数：
        array：待排序的数组

    返回：
        排序后的数组
    """

    if len(array) <= 1:
        return array

    # 选取基准元素
    pivot = array[0]

    # 分区
    left = []
    right = []
    for i in range(1, len(array)):
        if array[i] < pivot:
            left.append(array[i])
        else:
            right.append(array[i])

    # 递归排序
    return quick_sort(left) + [pivot] + quick_sort(right)

#### 代码逻辑分析

1. **选取基准元素：**代码中将数组的第一个元素作为基准元素。
2. **分区：**使用两个列表 `left` 和 `right` 分别存储比基准元素小和大的元素。
3. **递归排序：**对 `left` 和 `right` 列表分别进行快速排序，然后将排序后的结果合并。

#### 参数说明

* `array`：待排序的数组。

#### 复杂度分析

* **时间复杂度：**
* 最佳情况：O(n log n)
* 平均情况：O(n log n)
* 最差情况：O(n^2)
* **空间复杂度：**O(log n)，用于递归调用栈。

# 4. 排序算法应用**

**4.1 数组排序**

**4.1.1 应用场景**

数组排序是排序算法最常见的应用场景之一。数组是一种线性数据结构，其中元素按特定顺序存储。数组排序算法用于将数组中的元素重新排列为升序或降序。

**4.1.2 代码示例**

以下代码示例演示了如何使用 Java 中的 `Arrays.sort()` 方法对数组进行排序：

int[] arr = {5, 2, 8, 3, 1};
Arrays.sort(arr);
System.out.println(Arrays.toString(arr)); // 输出：[1, 2, 3, 5, 8]

**4.2 列表排序**

**4.2.1 应用场景**

列表是另一种线性数据结构，其中元素按插入顺序存储。与数组不同，列表可以动态增长和收缩。列表排序算法用于将列表中的元素重新排列为升序或降序。

**4.2.2 代码示例**

以下代码示例演示了如何使用 Python 中的 `sorted()` 函数对列表进行排序：

my_list = [5, 2, 8, 3, 1]
sorted_list = sorted(my_list)
print(sorted_list)  # 输出：[1, 2, 3, 5, 8]

**4.3 自定义对象排序**

**4.3.1 应用场景**

自定义对象排序算法用于对自定义对象进行排序。自定义对象通常具有多个属性，排序算法必须根据这些属性来确定对象的顺序。

**4.3.2 代码示例**

以下代码示例演示了如何使用 Java 中的 `Comparable` 接口对自定义对象进行排序：

class Person implements Comparable<Person> {
    private String name;
    private int age;

    public Person(String name, int age) {
        this.name = name;
        this.age = age;
    }

    @Override
    public int compareTo(Person other) {
        return this.age - other.age;
    }
}

List<Person> persons = new ArrayList<>();
persons.add(new Person("John", 30));
persons.add(new Person("Mary", 25));
persons.add(new Person("Bob", 40));
Collections.sort(persons);
System.out.println(persons); // 输出：[Mary, John, Bob]

# 5. 排序算法优化

### 5.1 时间复杂度优化

时间复杂度是衡量算法效率的重要指标，对于海量数据排序，时间复杂度优化尤为关键。

#### 5.1.1 算法选择

不同的排序算法具有不同的时间复杂度，在选择排序算法时，需要根据数据规模和数据分布特点进行综合考虑。

- **数据规模较小**（通常小于 10000 个元素）：冒泡排序、选择排序和插入排序的时间复杂度较低，可以满足要求。
- **数据规模较大**（通常大于 10000 个元素）：快速排序、归并排序和堆排序的时间复杂度较优，可以有效提升排序效率。

#### 5.1.2 数据结构选择

数据结构的选择也会影响排序算法的时间复杂度。

- **数组**：数组是一种连续存储结构，元素访问时间复杂度为 O(1)，适用于冒泡排序、选择排序和插入排序等原地排序算法。
- **链表**：链表是一种非连续存储结构，元素访问时间复杂度为 O(n)，不适用于原地排序算法。但链表可以利用其插入和删除操作的便利性，实现快速排序和归并排序等非原地排序算法。

### 5.2 空间复杂度优化

空间复杂度是指算法在运行过程中占用的内存空间。对于内存资源有限的系统，空间复杂度优化至关重要。

#### 5.2.1 原地排序算法

原地排序算法是指在不使用额外空间的情况下对原数组进行排序。冒泡排序、选择排序和插入排序都是原地排序算法。

#### 5.2.2 辅助空间优化

非原地排序算法可以通过优化辅助空间的使用来降低空间复杂度。

- **快速排序**：快速排序可以使用递归调用来实现，每次递归调用都会创建一个新的栈帧，占用额外的空间。可以通过使用非递归实现或尾递归优化来减少空间占用。
- **归并排序**：归并排序需要额外的空间来存储合并后的结果。可以通过使用原地归并算法来减少空间占用。

**代码示例：**

# 原地归并排序
def merge_sort_inplace(arr):
    # 将数组分成两部分
    mid = len(arr) // 2
    left = arr[:mid]
    right = arr[mid:]

    # 递归排序左右两部分
    merge_sort_inplace(left)
    merge_sort_inplace(right)

    # 合并左右两部分
    i = 0
    j = 0
    k = 0

    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            arr[k] = left[i]
            i += 1
        else:
            arr[k] = right[j]
            j += 1
        k += 1

    # 将剩余元素复制到数组中
    while i < len(left):
        arr[k] = left[i]
        i += 1
        k += 1

    while j < len(right):
        arr[k] = right[j]
        j += 1
        k += 1

**代码逻辑分析：**

该代码实现了原地归并排序算法。它将数组分成两部分，递归排序左右两部分，然后将排序后的两部分合并到原数组中。通过使用三个指针（i、j、k）在原数组中进行合并，避免了创建额外的空间。

# 6.1 并行排序

### 6.1.1 多线程排序

多线程排序通过将排序任务分配给多个线程来实现并行化。每个线程负责排序一部分数据，然后将结果合并为最终的排序结果。

**代码示例：**

import threading

def merge_sort(arr):
    if len(arr) <= 1:
        return arr

    mid = len(arr) // 2
    left_half = merge_sort(arr[:mid])
    right_half = merge_sort(arr[mid:])

    return merge(left_half, right_half)

def merge(left, right):
    i, j = 0, 0
    merged = []

    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            merged.append(left[i])
            i += 1
        else:
            merged.append(right[j])
            j += 1

    while i < len(left):
        merged.append(left[i])
        i += 1

    while j < len(right):
        merged.append(right[j])
        j += 1

    return merged

def parallel_merge_sort(arr, num_threads):
    if num_threads <= 1:
        return merge_sort(arr)

    mid = len(arr) // 2
    left_half = parallel_merge_sort(arr[:mid], num_threads // 2)
    right_half = parallel_merge_sort(arr[mid:], num_threads // 2)

    return merge(left_half, right_half)

# 使用 4 个线程对一个长度为 100000 的数组进行排序
arr = list(range(100000))
num_threads = 4
sorted_arr = parallel_merge_sort(arr, num_threads)

### 6.1.2 分布式排序

分布式排序将排序任务分配给多个分布式节点，每个节点负责排序一部分数据。然后，将各个节点的排序结果合并为最终的排序结果。

**流程图：**

graph LR
subgraph 分布式排序
    A[排序节点 1] --> B[合并]
    C[排序节点 2] --> B[合并]
    D[排序节点 3] --> B[合并]
end

**代码示例：**

import ray

@ray.remote
def sort_partition(arr, start, end):
    return sorted(arr[start:end])

def distributed_merge_sort(arr, num_partitions):
    # 将数组划分为多个分区
    partitions = [[] for _ in range(num_partitions)]
    partition_size = len(arr) // num_partitions
    for i in range(num_partitions):
        start = i * partition_size
        end = (i + 1) * partition_size
        partitions[i] = arr[start:end]

    # 在每个分区上并行排序
    sorted_partitions = ray.get([sort_partition.remote(partition, 0, len(partition)) for partition in partitions])

    # 合并排序结果
    sorted_arr = []
    for partition in sorted_partitions:
        sorted_arr.extend(partition)

    return sorted_arr

# 使用 4 个分布式节点对一个长度为 100000 的数组进行排序
arr = list(range(100000))
num_partitions = 4
ray.init()
sorted_arr = distributed_merge_sort(arr, num_partitions)