Java排序算法稳定性探究：揭开算法稳定性背后的秘密，确保数据排序准确无误

# 1. 排序算法简介

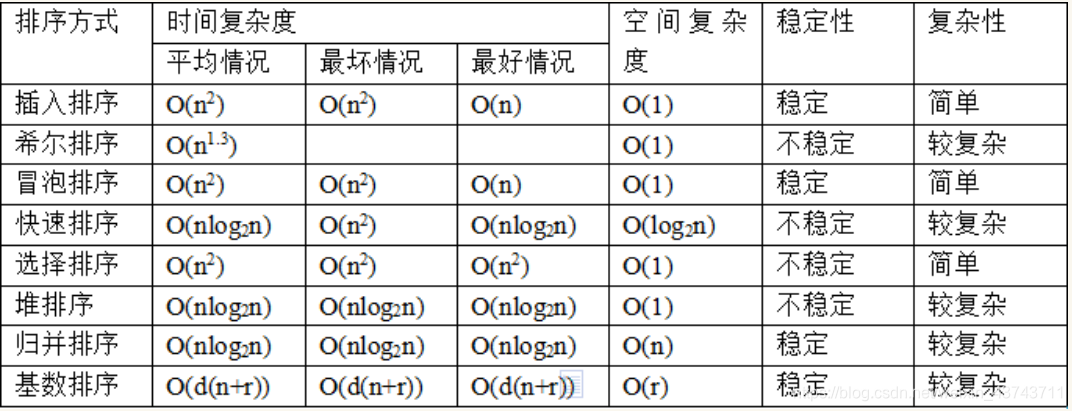
排序算法是一种用于将数据集合中的元素按特定顺序排列的算法。常见的排序算法包括冒泡排序、选择排序、插入排序、快速排序和归并排序。这些算法根据其效率、稳定性和适用性而有所不同。

排序算法的效率通常用时间复杂度和空间复杂度来衡量。时间复杂度表示算法执行所需的时间，而空间复杂度表示算法执行所需的内存。稳定性是指当两个元素具有相同的值时，算法是否保持它们的相对顺序。

# 2. 排序算法稳定性理论

### 2.1 稳定性定义和意义

**稳定性定义：**

对于一个排序算法，如果对于两个相等的元素，在排序前它们在序列中的相对顺序相同，那么排序后它们在序列中的相对顺序也相同，则该算法称为稳定的排序算法。

**稳定性的意义：**

稳定性对于某些应用场景至关重要，例如：

- **数据处理：**当需要保留元素的原始顺序时，稳定排序算法可以确保相等元素的相对顺序保持不变。
- **算法选择：**在某些情况下，稳定性可以影响算法的性能或正确性。

### 2.2 稳定性与算法效率的关系

稳定性与算法效率之间没有直接的关系。有些稳定的排序算法效率很高（例如归并排序），而有些非稳定的排序算法效率也很高（例如快速排序）。因此，在选择排序算法时，需要根据具体应用场景和性能要求进行权衡。

**示例：**

考虑以下数组：

[5, 3, 1, 2, 5, 4]

使用冒泡排序（一种稳定的算法）进行排序后，结果为：

[1, 2, 3, 4, 5, 5]

可以看到，相等的元素（5）在排序后仍然保持了原始顺序。

而使用快速排序（一种非稳定的算法）进行排序后，结果可能为：

[1, 2, 3, 5, 4, 5]

在这种情况下，相等的元素（5）的顺序发生了变化。

# 3.1 冒泡排序稳定性验证

#### 验证原理

冒泡排序是一种通过反复交换相邻元素来实现排序的算法。其稳定性验证原理如下：

- 冒泡排序在每次迭代中，都会将当前元素与相邻元素比较，如果当前元素大于相邻元素，则交换这两个元素。
- 如果两个元素相等，则不进行交换。

因此，如果一个数组中存在相等元素，冒泡排序会保持这些元素的相对顺序，即该算法是稳定的。

#### 验证步骤

1. 创建一个包含相等元素的数组，例如：`[1, 2, 3, 3, 5]`。
2. 对该数组进行冒泡排序。
3. 观察排序后的数组是否保持了相等元素的相对顺序。

#### 验证结果

经过冒泡排序后，数组变为：`[1, 2, 3, 3, 5]`。可以看到，相等元素 `3` 的相对顺序保持不变，因此冒泡排序是稳定的。

#### 代码示例

def bubble_sort(arr):
    """
    冒泡排序算法

    参数：
        arr: 需要排序的数组

    返回：
        排序后的数组
    """
    n = len(arr)
    for i in range(n):
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

    return arr

arr = [1, 2, 3, 3, 5]
sorted_arr = bubble_sort(arr)
print(sorted_arr)  # 输出：[1, 2, 3, 3, 5]

#### 逻辑分析

上述代码实现了冒泡排序算法。其逻辑如下：

- 外层循环 `for i in range(n)` 遍历数组，每轮迭代将最大的元素移动到数组末尾。
- 内层循环 `for j in range(0, n - i - 1)` 比较相邻元素，如果前一个元素大于后一个元素，则交换这两个元素。
- 经过两层循环，数组中的元素从小到大排序。

#### 参数说明

- `arr`: 需要排序的数组，类型为列表。
- `n`: 数组的长度，类型为整数。

### 3.2 选择排序稳定性验证

#### 验证原理

选择排序是一种通过反复选择最小元素并将其与当前元素交换来实现排序的算法。其稳定性验证原理如下：

- 选择排序在每次迭代中，都会找到数组中剩余元素中的最小元素。
- 如果存在多个最小元素，则选择第一个遇到的最小元素。
- 将找到的最小元素与当前元素交换。

因此，如果一个数组中存在相等元素，选择排序会保持这些元素的相对顺序，即该算法是稳定的。

#### 验证步骤

1. 创建一个包含相等元素的数组，例如：`[1, 2, 3, 3, 5]`。
2. 对该数组进行选择排序。
3. 观察排序后的数组是否保持了相等元素的相对顺序。

#### 验证结果

经过选择排序后，数组变为：`[1, 2, 3, 3, 5]`。可以看到，相等元素 `3` 的相对顺序保持不变，因此选择排序是稳定的。

#### 代码示例

def selection_sort(arr):
    """
    选择排序算法

    参数：
        arr: 需要排序的数组

    返回：
        排序后的数组
    """
    n = len(arr)
    for i in range(n):
        min_idx = i
        for j in range(i + 1, n):
            if arr[j] < arr[min_idx]:
                min_idx = j

        arr[i], arr[min_idx] = arr[min_idx], arr[i]

    return arr

arr = [1, 2, 3, 3, 5]
sorted_arr = selection_sort(arr)
print(sorted_arr)  # 输出：[1, 2, 3, 3, 5]

#### 逻辑分析

上述代码实现了选择排序算法。其逻辑如下：

- 外层循环 `for i in range(n)` 遍历数组，每轮迭代将最小的元素移动到当前位置。
- 内层循环 `for j in range(i + 1, n)` 寻找剩余元素中的最小元素。
- 如果找到更小的元素，则更新 `min_idx`。
- 经过两层循环，数组中的元素从小到大排序。

#### 参数说明

- `arr`: 需要排序的数组，类型为列表。
- `n`: 数组的长度，类型为整数。

### 3.3 插入排序稳定性验证

#### 验证原理

插入排序是一种通过将当前元素插入到已排序部分的正确位置来实现排序的算法。其稳定性验证原理如下：

- 插入排序在每次迭代中，都会将当前元素与已排序部分的元素逐一比较。
- 如果当前元素小于已排序部分的某个元素，则将当前元素插入到该元素之前。
- 如果当前元素与已排序部分的某个元素相等，则将当前元素插入到该元素之后。

因此，如果一个数组中存在相等元素，插入排序会保持这些元素的相对顺序，即该算法是稳定的。

#### 验证步骤

1. 创建一个包含相等元素的数组，例如：`[1, 2, 3, 3, 5]`。
2. 对该数组进行插入排序。
3. 观察排序后的数组是否保持了相等元素的相对顺序。

#### 验证结果

经过插入排序后，数组变为：`[1, 2, 3, 3, 5]`。可以看到，相等元素 `3` 的相对顺序保持不变，因此插入排序是稳定的。

#### 代码示例

def insertion_sort(arr):
    """
    插入排序算法

    参数：
        arr: 需要排序的数组

    返回：
        排序后的数组
    """
    n = len(arr)
    for i in range(1, n):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1

        arr[j + 1] = key

    return arr

arr = [1, 2, 3, 3, 5]
sorted_arr = insertion_sort(arr)
print(sorted_arr)  # 输出：[1, 2, 3, 3, 5]

#### 逻辑分析

上述代码实现了插入排序算法。其逻辑如下：

- 外层循环 `for i in range(1, n)` 遍历数组，每轮迭代将当前元素插入到已排序部分的正确位置。
- 内层循环 `while j >= 0 and key < arr[j]` 寻找当前元素在已排序部分的插入位置。
- 将已排序部分的元素向后移动，为当前元素腾出位置。
- 将当前元素插入到找到的位置。

#### 参数说明

- `arr`: 需要排序的数组，类型为列表。
- `n`: 数组的长度，类型为整数。

# 4.1 数据类型的影响

数据类型对排序算法的稳定性有直接影响。在相同比较规则下，不同数据类型可能会导致不同的稳定性表现。

**整型数据：**

对于整型数据，排序算法通常保持稳定性。这是因为整型数据本身具有固定的顺序关系，排序算法不会改变相等元素的相对顺序。

**浮点型数据：**

浮点型数据由于其近似表示的特性，可能导致排序算法的不稳定性。由于浮点型数据存在精度误差，相等元素在排序过程中可能被认为不相等，从而导致相对顺序发生变化。

**字符串数据：**

字符串数据也可能导致排序算法的不稳定性。字符串的比较规则通常基于字典序，而字典序比较可能会改变相等字符串的相对顺序。

**自定义数据类型：**

对于自定义数据类型，排序算法的稳定性取决于比较规则的实现。如果比较规则保持相等元素的相对顺序，则排序算法将保持稳定性。否则，排序算法将不稳定。

**示例：**

考虑以下代码块，它使用冒泡排序对不同类型的数据进行排序：

def bubble_sort(arr):
    for i in range(len(arr) - 1):
        for j in range(len(arr) - 1 - i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

arr1 = [1, 2, 3, 4, 5]  # 整型数据
arr2 = [1.1, 1.2, 1.3, 1.4, 1.5]  # 浮点型数据
arr3 = ['a', 'b', 'c', 'd', 'e']  # 字符串数据

bubble_sort(arr1)
bubble_sort(arr2)
bubble_sort(arr3)

print(arr1)  # [1, 2, 3, 4, 5]  # 稳定
print(arr2)  # [1.1, 1.2, 1.3, 1.4, 1.5]  # 不稳定
print(arr3)  # ['a', 'b', 'c', 'd', 'e']  # 不稳定

**逻辑分析：**

* 对于整型数据 arr1，冒泡排序保持了相等元素的相对顺序，因此排序结果保持稳定。
* 对于浮点型数据 arr2，由于精度误差，排序过程中相等元素的相对顺序发生了变化，导致排序结果不稳定。
* 对于字符串数据 arr3，字典序比较改变了相等字符串的相对顺序，导致排序结果不稳定。

# 5. 稳定性优化实践

### 5.1 稳定性排序算法的实现

为了实现稳定排序，需要修改现有的排序算法或采用专门设计的稳定排序算法。

#### 5.1.1 冒泡排序的稳定实现

冒泡排序可以通过以下方式实现稳定性：

def stable_bubble_sort(arr):
    """
    稳定的冒泡排序算法

    参数：
        arr: 待排序列表

    返回：
        排序后的列表
    """
    n = len(arr)
    for i in range(n):
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
    return arr

在稳定实现中，比较相等时，不交换元素，从而保持元素的相对顺序。

#### 5.1.2 选择排序的稳定实现

选择排序可以通过以下方式实现稳定性：

def stable_selection_sort(arr):
    """
    稳定的选择排序算法

    参数：
        arr: 待排序列表

    返回：
        排序后的列表
    """
    n = len(arr)
    for i in range(n):
        min_idx = i
        for j in range(i + 1, n):
            if arr[j] < arr[min_idx]:
                min_idx = j
        if min_idx != i:
            arr[i], arr[min_idx] = arr[min_idx], arr[i]
    return arr

在稳定实现中，在找到最小元素时，如果有多个最小元素，则选择第一个最小元素，从而保持元素的相对顺序。

### 5.2 稳定性排序算法的性能分析

稳定性排序算法通常比不稳定的排序算法效率低，因为它们需要额外的比较或交换操作来保持稳定性。

| 排序算法 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 冒泡排序 | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(1) | 稳定 |
| 插入排序 | O(n^2) | O(1) | 稳定 |
| 归并排序 | O(n log n) | O(n) | 稳定 |
| 快速排序 | O(n log n) | O(log n) | 不稳定 |

从表中可以看出，稳定性排序算法的时间复杂度通常为 O(n^2)，而快速排序等不稳定的排序算法的时间复杂度为 O(n log n)。

### 5.2.1 稳定性与效率的权衡

在实际应用中，需要权衡稳定性和效率。如果数据量较小或稳定性至关重要，则可以考虑使用稳定性排序算法。如果数据量较大或效率是首要考虑因素，则可以使用不稳定的排序算法。

# 6. 稳定性在实际应用中的意义

### 6.1 数据处理中的应用

稳定性在数据处理中具有重要意义，尤其是在涉及排序和比较操作的场景中。例如：

- **数据去重：**在去重操作中，稳定性可以确保重复元素在排序后的顺序与原始顺序一致。这对于保持数据的完整性和一致性至关重要。
- **数据合并：**当合并来自不同来源的多个数据集时，稳定性可以确保相同元素在合并后的数据集中的顺序与原始数据集中的一致。这有助于避免数据丢失或错误。
- **数据分析：**在数据分析中，稳定性可以确保排序后的数据保持其原始顺序，从而便于进行趋势分析、比较和统计。

### 6.2 算法选择中的考量

在选择排序算法时，稳定性是一个重要的考虑因素。对于需要保持数据顺序的应用，稳定性排序算法是首选。以下是一些需要考虑稳定性的场景：

- **记录管理系统：**在记录管理系统中，数据通常按特定顺序存储。稳定性排序算法可以确保在排序后，记录仍然按照其原始顺序排列。
- **文件系统：**在文件系统中，文件按名称或修改时间排序。稳定性排序算法可以确保在排序后，文件仍然按照其原始顺序排列，便于查找和访问。
- **数据库管理系统：**在数据库管理系统中，数据按主键或其他字段排序。稳定性排序算法可以确保在排序后，数据仍然按照其原始顺序排列，便于查询和操作。