揭秘MATLAB直线拟合的幕后黑科技：原理、方法和优化秘诀

# 1. MATLAB直线拟合概述

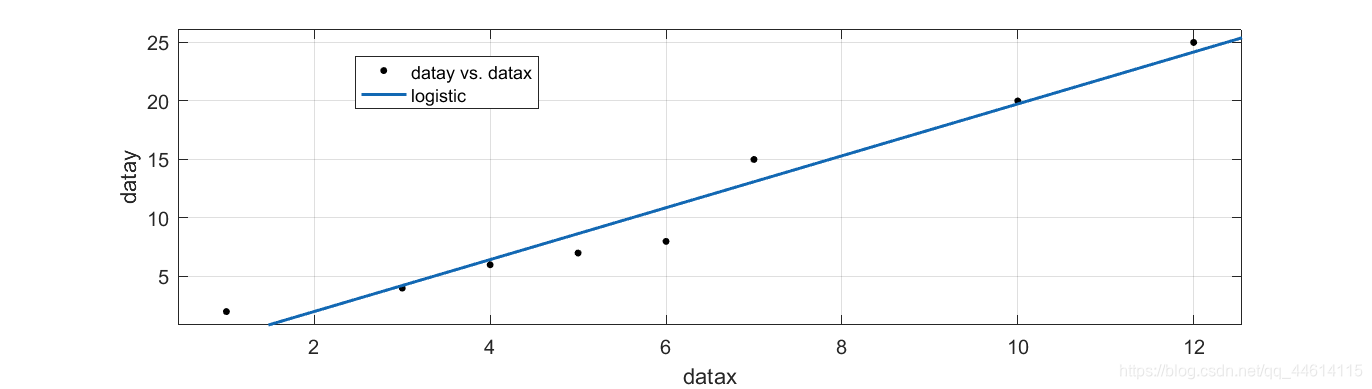
MATLAB直线拟合是一种强大的工具，用于确定一组数据点的最佳拟合直线。它在各种领域都有应用，包括数据分析、预测建模和机器学习。直线拟合的目标是找到一条直线，以最小化数据点与直线之间的垂直距离之和。这种方法称为最小二乘法，它产生一条最佳拟合直线，可以用来描述数据中的趋势或模式。

# 2. 直线拟合理论基础

### 2.1 最小二乘法原理

最小二乘法是直线拟合最常用的方法，其原理是找到一条直线，使得所有数据点到该直线的垂直距离的平方和最小。

**数学公式：**

min ∑(y_i - a*x_i - b)^2

其中：

* (x_i, y_i) 为数据点
* a 为直线斜率
* b 为直线截距

**求解方法：**

最小二乘法问题的求解可以通过以下线性方程组：

[n ∑x_i ∑x_i^2] [a] = [∑y_i]
[∑x_i ∑x_i^2 ∑x_i^3] [b] = [∑x_iy_i]

### 2.2 相关系数和决定系数

**相关系数（r）：**

相关系数衡量数据点与拟合直线之间的线性相关性。其取值范围为[-1, 1]：

* r = 1：完全正相关
* r = 0：无相关性
* r = -1：完全负相关

**决定系数（R^2）：**

决定系数表示拟合直线解释数据方差的百分比。其取值范围为[0, 1]：

* R^2 = 1：拟合直线完美拟合数据
* R^2 = 0：拟合直线无法解释数据方差

### 2.3 拟合优度的评估

**均方误差（MSE）：**

均方误差衡量拟合直线与数据点之间的平均平方距离。

**数学公式：**

MSE = 1/n ∑(y_i - a*x_i - b)^2

**残差平方和（RSS）：**

残差平方和是所有数据点到拟合直线的垂直距离的平方和。

**数学公式：**

RSS = ∑(y_i - a*x_i - b)^2

**总平方和（TSS）：**

总平方和是所有数据点到其平均值的垂直距离的平方和。

**数学公式：**

TSS = ∑(y_i - y_mean)^2

**拟合优度（R^2）：**

拟合优度是决定系数的平方根，表示拟合直线解释数据方差的百分比。

**数学公式：**

R^2 = 1 - RSS/TSS

# 3. MATLAB直线拟合方法

### 3.1 polyfit函数

polyfit函数用于拟合多项式曲线，其中一阶多项式即为直线。其语法格式为：

p = polyfit(x, y, n)

其中：

* x：自变量数据向量
* y：因变量数据向量
* n：拟合多项式的阶数，对于直线拟合，n=1

**代码块：**

% 数据准备
x = [1, 2, 3, 4, 5];
y = [2, 4, 5, 4, 5];

% 直线拟合
p = polyfit(x, y, 1);

% 输出拟合参数
disp(p);

**逻辑分析：**

* 第1行：定义自变量x和因变量y的数据向量。
* 第3行：使用polyfit函数拟合一阶多项式（直线）。
* 第5行：输出拟合参数p，其中p(1)为斜率，p(2)为截距。

### 3.2 fitlm函数

fitlm函数用于拟合线性模型，包括直线拟合。其语法格式为：

model = fitlm(x, y)

其中：

* x：自变量数据矩阵或表
* y：因变量数据向量或表

**代码块：**

% 数据准备
x = [1, 2, 3, 4, 5]';
y = [2, 4, 5, 4, 5]';

% 直线拟合
model = fitlm(x, y);

% 输出拟合参数
disp(model.Coefficients.Estimate);

**逻辑分析：**

* 第1行：定义自变量x和因变量y的数据向量。
* 第3行：使用fitlm函数拟合线性模型。
* 第5行：输出拟合参数，其中Coefficients.Estimate(1)为斜率，Coefficients.Estimate(2)为截距。

### 3.3 lsqcurvefit函数

lsqcurvefit函数用于拟合非线性曲线，但也可以用于直线拟合。其语法格式为：

[p, resnorm, residual, exitflag] = lsqcurvefit(fun, p0, x, y)

其中：

* fun：拟合函数，对于直线拟合，fun=@(p,x) p(1)*x + p(2)
* p0：初始拟合参数
* x：自变量数据向量
* y：因变量数据向量

**代码块：**

% 数据准备
x = [1, 2, 3, 4, 5];
y = [2, 4, 5, 4, 5];

% 拟合函数
fun = @(p,x) p(1)*x + p(2);

% 初始参数
p0 = [1, 1];

% 直线拟合
[p, resnorm, residual, exitflag] = lsqcurvefit(fun, p0, x, y);

% 输出拟合参数
disp(p);

**逻辑分析：**

* 第1行：定义自变量x和因变量y的数据向量。
* 第3行：定义拟合函数fun。
* 第5行：定义初始拟合参数p0。
* 第7行：使用lsqcurvefit函数拟合直线。
* 第9行：输出拟合参数p，其中p(1)为斜率，p(2)为截距。

# 4. 直线拟合实践应用

### 4.1 数据预处理和特征提取

在进行直线拟合之前，数据预处理和特征提取至关重要。数据预处理包括数据清洗、归一化和标准化，以确保数据的质量和一致性。特征提取则涉及从原始数据中提取与拟合目标相关的特征。

**数据清洗**

数据清洗旨在去除异常值、缺失值和噪声，以提高拟合的准确性。异常值可以通过统计方法（如 Grubbs 检验）或可视化（如箱线图）识别。缺失值可以通过插值或删除来处理，具体取决于数据的性质和拟合目标。

**归一化和标准化**

归一化和标准化可以将数据缩放到统一的范围，以消除不同特征之间的量纲差异。归一化将数据映射到 [0, 1] 区间，而标准化将数据映射到均值为 0、标准差为 1 的正态分布。

**特征提取**

特征提取从原始数据中提取与拟合目标相关的特征。对于直线拟合，通常使用自变量 (x) 和因变量 (y) 作为特征。此外，还可以提取其他特征，例如自变量的二次方或与因变量相关的其他变量。

### 4.2 拟合模型的选择和参数优化

选择合适的拟合模型和优化模型参数对于获得准确的拟合结果至关重要。

**拟合模型的选择**

对于直线拟合，通常使用线性回归模型，即 y = mx + b。然而，对于非线性数据，可能需要使用非线性模型，例如多项式回归或指数回归。

**参数优化**

拟合模型的参数可以通过最小化残差平方和 (RSS) 来优化。RSS 是预测值和实际值之间的差值的平方和。优化算法，例如梯度下降或牛顿法，可以用来找到使 RSS 最小的参数值。

### 4.3 拟合结果的分析和可视化

拟合结果的分析和可视化可以评估拟合的准确性和可靠性。

**拟合优度的评估**

拟合优度可以通过相关系数 (R)、决定系数 (R^2) 和均方根误差 (RMSE) 等指标来评估。R 和 R^2 表示拟合线与数据点的拟合程度，而 RMSE 表示预测值与实际值之间的平均误差。

**可视化**

拟合结果可以通过散点图和拟合线进行可视化。散点图显示原始数据点，而拟合线表示拟合模型。可视化可以帮助识别异常值、评估拟合的准确性和识别潜在的非线性趋势。

**代码示例**

以下 MATLAB 代码演示了直线拟合的实践应用：

% 数据预处理
data = [1, 2, 3, 4, 5; 2, 4, 6, 8, 10];
data = normalize(data, 'range'); % 归一化

% 拟合模型的选择和参数优化
model = fitlm(data(1, :), data(2, :)); % 使用线性回归模型

% 拟合结果的分析和可视化
R = model.Rsquared.Ordinary; % 相关系数
R2 = model.Rsquared.Adjusted; % 决定系数
RMSE = sqrt(model.MSE); % 均方根误差

figure;
scatter(data(1, :), data(2, :));
hold on;
plot(data(1, :), model.predict(data(1, :)), 'r'); % 拟合线
xlabel('x');
ylabel('y');
title('直线拟合结果');
legend('数据点', '拟合线');

# 5. 直线拟合进阶技巧

### 5.1 加权最小二乘法

在某些情况下，数据点可能具有不同的重要性或可靠性。为了解决这个问题，可以采用加权最小二乘法，其中每个数据点都赋予一个权重，以反映其重要性。权重较高的数据点在拟合过程中将发挥更大的作用。

**代码块：**

% 数据点和权重
x = [1, 2, 3, 4, 5];
y = [2, 4, 5, 4, 6];
w = [1, 2, 3, 4, 5];

% 加权最小二乘法拟合
[p, S] = polyfit(x, y, 1, w);

% 绘制拟合曲线
plot(x, y, 'o');
hold on;
plot(x, polyval(p, x), 'r-');

**逻辑分析：**

* `polyfit` 函数的第四个参数 `w` 指定了数据点的权重。
* `S` 变量包含拟合结果的统计信息，包括协方差矩阵和残差平方和。

### 5.2 非线性拟合

直线拟合是一种线性拟合，其中拟合曲线是一条直线。然而，在某些情况下，数据可能表现出非线性趋势。对于这种情况，可以使用非线性拟合，其中拟合曲线可以是任何类型的函数。

**代码块：**

% 数据点
x = [1, 2, 3, 4, 5];
y = [2, 4, 8, 16, 32];

% 非线性拟合模型（指数函数）
model = @(p, x) p(1) * exp(p(2) * x);

% 拟合参数
p0 = [1, 0.5];

% 非线性最小二乘法拟合
[p, resnorm, residual, exitflag] = lsqcurvefit(model, p0, x, y);

% 绘制拟合曲线
plot(x, y, 'o');
hold on;
plot(x, model(p, x), 'r-');

**逻辑分析：**

* `lsqcurvefit` 函数用于非线性最小二乘法拟合。
* `model` 函数定义了非线性拟合模型。
* `p0` 变量指定了拟合参数的初始值。
* `resnorm` 变量包含残差平方和。
* `residual` 变量包含拟合残差。
* `exitflag` 变量指示拟合是否成功。

### 5.3 多项式拟合

多项式拟合是一种特殊类型的非线性拟合，其中拟合曲线是一条多项式。多项式拟合可以用于拟合具有复杂趋势的数据。

**代码块：**

% 数据点
x = [1, 2, 3, 4, 5];
y = [2, 4, 8, 16, 32];

% 多项式拟合（二次多项式）
p = polyfit(x, y, 2);

% 绘制拟合曲线
plot(x, y, 'o');
hold on;
plot(x, polyval(p, x), 'r-');

**逻辑分析：**

* `polyfit` 函数用于多项式拟合。
* `p` 变量包含拟合多项式的系数。
* `polyval` 函数用于计算多项式在给定点的值。

# 6. MATLAB直线拟合优化秘诀

### 6.1 算法选择和参数调整

在MATLAB中进行直线拟合时，选择合适的算法和调整其参数对于获得最佳拟合结果至关重要。MATLAB提供了多种算法，每种算法都有其独特的优点和缺点。

| 算法 | 优点 | 缺点 |
|---|---|---|
| `polyfit` | 快速、简单 | 可能不适用于非线性数据 |
| `fitlm` | 稳健、可用于加权最小二乘法 | 对于大型数据集可能较慢 |
| `lsqcurvefit` | 可用于非线性拟合 | 需要指定初始参数 |

除了选择算法外，还可以调整算法的参数以优化拟合结果。例如，`polyfit`函数允许指定多项式的阶数，而`fitlm`函数允许指定权重矩阵。通过调整这些参数，可以提高拟合的准确性。

### 6.2 数据清洗和异常值处理

在进行直线拟合之前，对数据进行清洗和处理非常重要。这包括删除异常值、处理缺失值以及转换数据以提高线性度。

异常值是指明显偏离其他数据点的极端值。这些值可能会对拟合结果产生重大影响，因此在拟合之前应将其删除。可以使用以下代码删除异常值：

% 识别异常值
outliers = isoutlier(data);

% 删除异常值
data(outliers, :) = [];

缺失值是指数据集中缺少的值。这些值可以通过插值或删除来处理。插值是指使用其他数据点估计缺失值，而删除是指简单地从数据集中删除缺失值。

转换数据以提高线性度可以改善拟合结果。例如，如果数据呈指数分布，则可以通过取对数来将其线性化。

### 6.3 拟合结果的验证和改进

拟合结果的验证和改进是确保拟合模型准确性和可靠性的重要步骤。以下是一些验证和改进拟合结果的方法：

* **交叉验证：**将数据集分成训练集和测试集，并在测试集上评估拟合模型的性能。
* **残差分析：**检查拟合模型的残差（实际值与拟合值之间的差值）是否随机分布。如果残差呈非随机模式，则可能表明模型存在问题。
* **参数敏感性分析：**改变拟合模型的参数，并观察对拟合结果的影响。这可以帮助确定模型对参数变化的敏感性。

通过验证和改进拟合结果，可以确保拟合模型准确可靠，并可用于预测和决策。