MATLAB直线拟合在金融建模中的预测力：趋势分析和预测

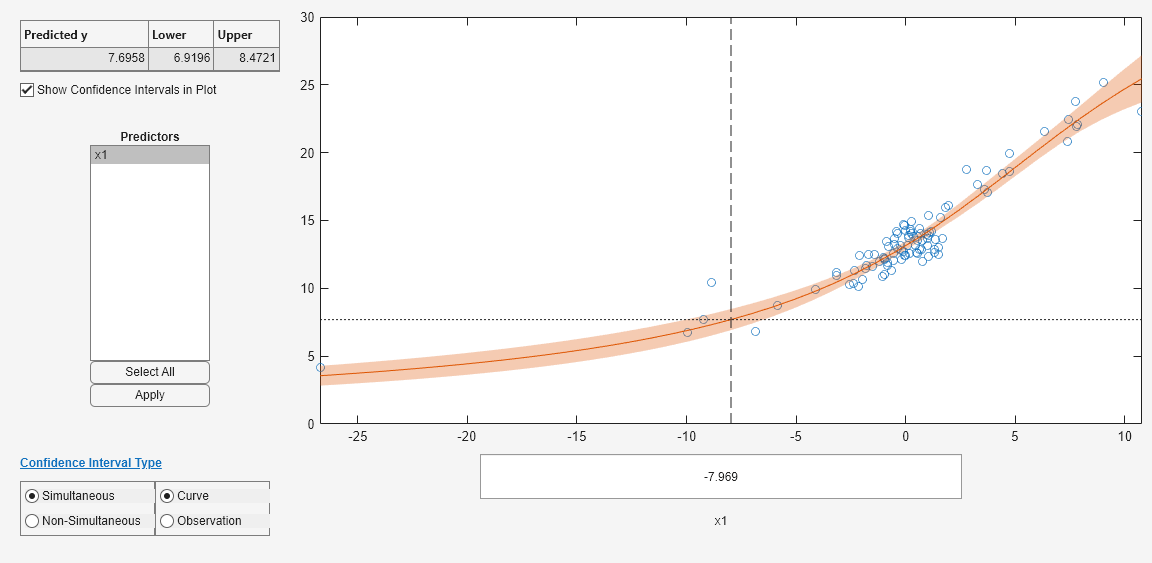
# 1. MATLAB直线拟合概述**

MATLAB直线拟合是一种强大的技术，用于确定给定数据集中的线性关系。它涉及到拟合一条直线到数据点，以预测未知值的趋势。直线拟合在金融建模中广泛应用，用于分析股票价格趋势、预测经济指标等。

MATLAB提供了广泛的函数来执行直线拟合，包括`polyfit`和`fitlm`。这些函数使用最小二乘法算法，通过最小化数据点和拟合直线之间的平方误差来确定最佳拟合直线。

# 2. 直线拟合理论基础

### 2.1 线性回归模型

线性回归模型是一种统计模型，用于预测一个或多个自变量与一个因变量之间的线性关系。在金融建模中，线性回归模型常用于预测股票价格、经济指标等。

线性回归模型的方程为：

y = β0 + β1x + ε

其中：

* y 为因变量
* x 为自变量
* β0 为截距
* β1 为斜率
* ε 为误差项

### 2.2 最小二乘法

最小二乘法是一种用于估计线性回归模型参数的方法。其目标是找到一组参数，使模型预测值与实际值之间的平方和最小。

最小二乘法的计算公式为：

β1 = (Σ(xi - x̄)(yi - ȳ)) / Σ(xi - x̄)^2
β0 = ȳ - β1x̄

其中：

* β1 为斜率
* β0 为截距
* xi 为自变量的第 i 个值
* yi 为因变量的第 i 个值
* x̄ 为自变量的平均值
* ȳ 为因变量的平均值

### 2.3 拟合优度评价指标

为了评估线性回归模型的拟合优度，可以使用以下指标：

* **决定系数 (R^2)**：衡量模型解释因变量变异的程度，范围为 0 到 1，值越大表示拟合越好。
* **均方根误差 (RMSE)**：衡量模型预测值与实际值之间的平均误差，值越小表示拟合越好。
* **平均绝对误差 (MAE)**：衡量模型预测值与实际值之间的平均绝对误差，值越小表示拟合越好。

**代码块：**

% 导入数据
data = readtable('stock_prices.csv');

% 提取自变量和因变量
x = data.date;
y = data.price;

% 构建线性回归模型
model = fitlm(x, y);

% 输出模型参数
disp('模型参数：');
disp(['截距：', num2str(model.Coefficients.Estimate(1))]);
disp(['斜率：', num2str(model.Coefficients.Estimate(2))]);

% 评估模型拟合优度
disp('模型拟合优度：');
disp(['R^2：', num2str(model.Rsquared.Ordinary)]);
disp(['RMSE：', num2str(model.RMSE)]);
disp(['MAE：', num2str(model.MAE)]);

**代码逻辑分析：**

* 使用 `readtable()` 函数导入数据。
* 提取自变量 `x`（日期）和因变量 `y`（价格）。
* 使用 `fitlm()` 函数构建线性回归模型。
* 输出模型参数，包括截距和斜率。
* 使用 `Rsquared.Ordinary`、`RMSE` 和 `MAE` 属性评估模型拟合优度。

# 3. MATLAB直线拟合实践

### 3.1 数据导入和预处理

**数据导入**

MATLAB提供了多种数据导入函数，如`importdata`、`csvread`和`xlsread`。选择合适的方法取决于数据的格式和来源。例如，如果数据存储在