概率分布优化：寻找数据模型的最优概率解决方案

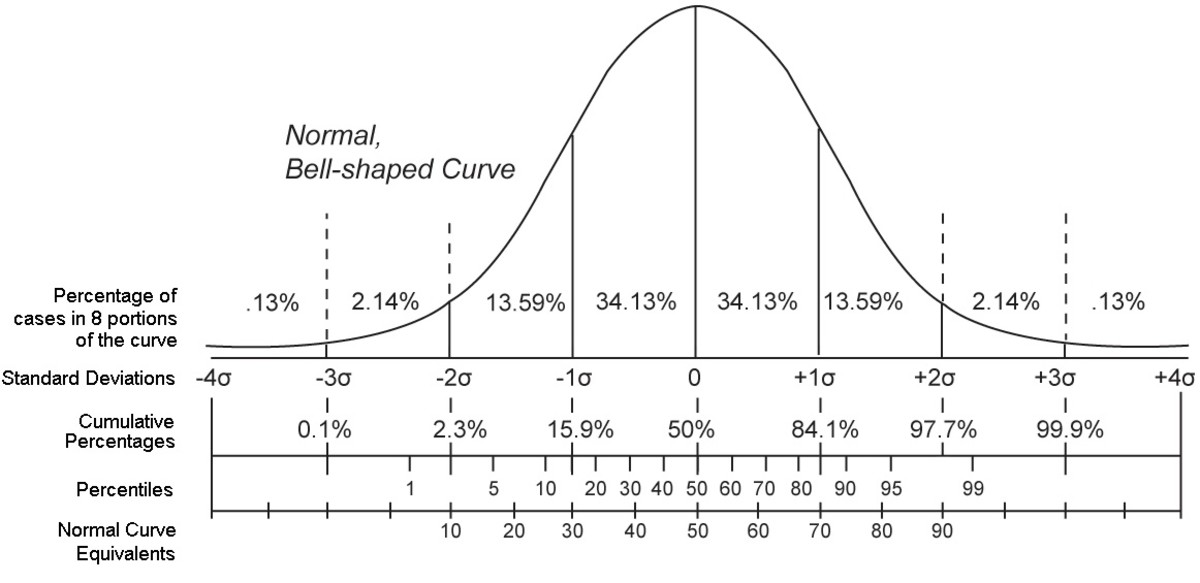
# 1. 概率分布基础与应用场景

在探索数据的世界中，概率分布是理解随机变量行为的关键。本章旨在为读者提供概率分布的基本概念及其在多个领域中的应用概览。

## 概率分布简介

概率分布是数学统计学的一个重要分支，它描述了一个随机变量可能取值的概率。这些分布能够帮助我们了解数据的形态、中心趋势、波动性以及它们的异常值。理解各种概率分布对于数据科学家、分析师、工程师以及任何涉及数据处理的专业人士来说都是至关重要的。

## 常见的概率分布类型

在实际应用中，我们会遇到不同类型的概率分布，比如二项分布、正态分布等。这些分布在不同的应用场景中扮演着核心角色：

- **离散型概率分布**：这类分布通常用于描述离散型随机变量的情况，如抛硬币得到正面的次数（二项分布）或不同号码在抽奖中被抽中的概率（多项分布）。

- **连续型概率分布**：用于描述连续变量，比如测量的误差（高斯分布/正态分布），或者个体的身高和体重（伽玛分布）。

概率分布不仅能帮助我们预测未来事件的概率，还能使我们能够更好地理解和解释数据。在接下来的章节中，我们将深入了解这些分布的理论，并探讨它们在实际问题解决中的应用。

# 2. 概率分布理论详解

在数据分析和统计推断中，概率分布是理解随机变量行为的基础。概率分布不仅可以描述单个随机变量的行为，还可以描述多个随机变量之间的关系。本章将深入探讨概率分布的理论，包括不同类型的概率分布、它们的数学特性以及多变量概率分布的处理方式。

## 2.1 常见的概率分布类型

概率分布根据随机变量的性质可以分为两大类：离散型概率分布和连续型概率分布。下面我们分别对这两种分布类型进行详细介绍。

### 2.1.1 离散型概率分布

离散型概率分布描述的是随机变量取有限或可数无限多个值的概率。最常见的一些离散型概率分布包括二项分布、泊松分布和几何分布等。

#### 二项分布

二项分布是离散概率分布中最基本的一种，它适用于描述固定次数的独立实验中成功的次数。二项分布有两个参数：试验次数 \(n\) 和每次试验成功的概率 \(p\)。

- 公式：
\[
P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}
\]
其中 \(\binom{n}{k}\) 是组合数，表示从 \(n\) 次实验中选取 \(k\) 次成功的组合方式数量。

- 应用：在质量控制中，二项分布可以用来确定在一定生产数量的产品中不合格品的数量。

#### 泊松分布

泊松分布通常用于描述单位时间或单位面积内发生的某随机事件的次数。

- 公式：
\[
P(X = k) = \frac{e^{-\lambda} \lambda^k}{k!}
\]
其中，\(\lambda\) 是单位时间（或单位面积）内事件平均发生的次数。

- 应用：比如，在电话呼叫中心，泊松分布可以用来预测在特定时间接到的呼叫数量。

#### 几何分布

几何分布用于描述重复独立实验中，试验成功前需要进行的试验次数。

- 公式：
\[
P(X = k) = (1-p)^{k-1}p
\]
其中 \(p\) 是每次试验成功的概率。

- 应用：在机器维护中，几何分布可以用来预计下一次机器故障前需要的正常运行时间。

### 2.1.2 连续型概率分布

连续型概率分布描述的是随机变量取连续值的概率。连续型分布中最常见的包括正态分布、均匀分布和指数分布等。

#### 正态分布

正态分布是最重要的一种连续型概率分布，许多自然和社会现象都近似服从正态分布。

- 公式：
\[
f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
\]
其中，\(\mu\) 和 \(\sigma\) 分别是分布的均值和标准差。

- 应用：在质量控制中，正态分布用来分析生产过程的稳定性。在金融中，正态分布用于估计投资回报的风险。

#### 均匀分布

均匀分布描述的是在某个区间内随机变量取值的概率是均匀的。

- 公式：
\[
f(x) = \frac{1}{b-a}, \quad a \leq x \leq b
\]
其中 \(a\) 和 \(b\) 是分布的区间边界。

- 应用：在模拟实验中，均匀分布用于生成随机数。

#### 指数分布

指数分布用于描述某事件发生的时间间隔，常用于可靠性工程和排队论。

- 公式：
\[
f(x) = \lambda e^{-\lambda x}, \quad x \geq 0
\]
其中 \(\lambda\) 是事件发生率。

- 应用：指数分布可以用来预测产品的使用寿命。

## 2.2 概率分布的数学特性

了解概率分布的数学特性对于数据分析至关重要。这些特性包括均值、方差、标准差、偏度和峰度等。

### 2.2.1 均值、方差和标准差

均值（期望值）是随机变量取值的平均数，它是衡量概率分布中心位置的指标。方差衡量的是随机变量取值的分散程度，而标准差是方差的平方根。

- 均值：
\[
\mu = E(X) = \sum_{x} x P(X = x)
\]
对于连续型分布：
\[
\mu = E(X) = \int_{-\infty}^{\infty} x f(x) dx
\]

- 方差：
\[
\sigma^2 = Var(X) = E[(X - \mu)^2]
\]

- 标准差：
\[
\sigma = \sqrt{Var(X)}
\]

### 2.2.2 偏度和峰度

偏度衡量的是概率分布的对称性，而峰度则衡量的是分布的尖峭程度。

- 偏度：
\[
Skewness = E\left[\left(\frac{X - \mu}{\sigma}\right)^3\right]
\]

- 峰度：
\[
Kurtosis = E\left[\left(\frac{X - \mu}{\sigma}\right)^4\right]
\]

偏度和峰度的计算对于理解数据集的形状和分布的异常值具有重要意义。

## 2.3 多变量概率分布

在实际应用中，我们经常遇到多个随机变量共同作用的情况，多变量概率分布描述了这些变量的联合行为。

### 2.3.1 联合概率分布

联合概率分布描述了两个或更多随机变量同时发生的概率。例如，两个随机变量 \(X\) 和 \(Y\) 的联合概率分布可以表示为 \(P(X = x \text{ and } Y = y)\)。

### 2.3.2 条件概率分布

条件概率分布是指在已知某些随机变量取值的条件下，其他随机变量取值的概率。对于随机变量 \(X\) 和 \(Y\)，条件概率分布 \(P(X|Y=y)\) 表示当 \(Y=y\) 时 \(X\) 的概率分布。

### 2.3.3 边缘概率分布

边缘概率分布是通过将联合概率分布中的某些变量求和或积分得到的。对于两个随机变量 \(X\) 和 \(Y\)，\(X\) 的边缘概率分布为：
\[P(X = x) = \sum_{y} P(X = x \text{ and } Y = y)\]
对于连续型变量，求和被积分替代。

在处理实际问题时，多变量概率分布提供了更为全面的视角，能够帮助我们理解和预测变量间的相互关系和影响。在后续章节中，我们将探讨如何对概率分布进行参数估计，并进一步优化这些估计方法。

# 3. 概率分布的参数估计方法

参数估计是统计学中的核心概念之一，它指的是根据样本数据来推断总体分布参数的过程。在实际应用中，参数估计允许我们使用观测数据来推断未知参数，如均值、方差等，这对于概率分布模型的建立至关重要。

#### 3.1 点估计

点估计是参数估计的一种形式，它提供了一个单一的估计值来代表总体参数。点估计的目的是找到最能代表总体参数的样本统计量。

##### 3.1.1 估计量的选择标准

选择一个合理的估计量是点估计的关键步骤。有效的估计量通常需要满足以下三个基本标准：

- 无偏性（Unbiasedness）：估计量的期望值应该等于真实参数值。无偏估计量在重复抽样时不会系统地高估或低估参数。
- 一致性（Consistency）：随着样本量的增大，估计量应该越来越接近总体参数的真实值。一致性保证了大规模抽样时估计量的稳定性和可靠性。
- 有效性（Efficiency）：在所有无偏估计量中，具有最小方差的估计量被认为是最有效的。有效性衡量了估计量对样本数据变化的敏感程度。

##### 3.1.2 常用的点估计方法

- 方法一：矩估计（Method of Moments）
矩估计是一种通过