Python绘制概率分布图：概率分布图解教程

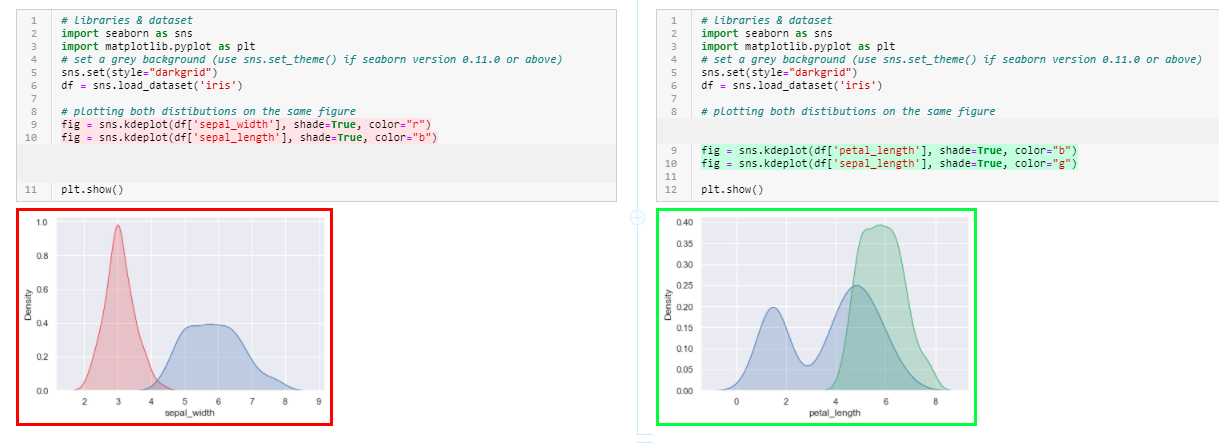
# 1. 概率分布图概述

在数据分析和统计学中，概率分布图是理解数据分布特性的关键工具。本章将对概率分布图进行概述，包括其定义、作用以及在不同应用场景中的重要性。此外，我们还将简要介绍概率分布图与概率论、随机变量的关系，为接下来的深入探讨奠定基础。

概率分布图是一种图形化的统计工具，用于展示随机变量的取值概率。它们是概率论中最重要的组成部分之一，能够帮助我们直观地理解数据的分布特征。通过概率分布图，我们可以对数据集进行初步分析，比如识别其分布的偏态、峰态以及异常值。

在数据科学和统计分析的实践中，概率分布图不仅有助于探索数据集的内在结构，而且对于建立预测模型和检验假设来说至关重要。通过对不同概率分布图的观察，我们可以推测数据的生成机制，并对数据的未来行为进行预测。

下面的章节将深入探讨概率分布图的理论基础，以及如何运用Python绘图库来绘制这些图表。

# 2. 概率论基础知识

## 2.1 随机变量与概率分布

### 2.1.1 随机变量的定义

随机变量是概率论中一个核心的概念，它是将随机试验的结果映射到实数线上的一个函数。简单来说，随机变量指的是一个变量，它可以取不同的值，其结果取决于随机事件的发生。在形式上，随机变量通常用大写字母，如X、Y或Z来表示。

随机变量可以分为两大类：离散型随机变量和连续型随机变量。

- 离散型随机变量：只能取有限个或可数无限个值，例如抛硬币的结果（正面或反面）。
- 连续型随机变量：可以取无限多个值，例如测量某物体的长度或质量。

### 2.1.2 概率分布的种类和特点

概率分布描述的是随机变量取各种可能值的概率。每一种概率分布都有其特定的性质和应用场景。

- 离散型概率分布：
- 二项分布：描述在固定次数的独立实验中成功次数的概率分布，适用于如抛硬币、产品检验等场景。
- 泊松分布：描述在固定时间或空间内随机事件发生的次数的概率分布，广泛用于电话呼叫、交通事故等领域的模拟。
- 几何分布：描述的是在一系列独立的伯努利试验中，首次成功发生前失败次数的概率分布，常用于排队理论和生存分析。

- 连续型概率分布：
- 正态分布（高斯分布）：描述了许多自然和社会科学领域中随机变量的分布情况，是自然界和社会现象中最为常见的分布类型。
- 指数分布：通常用来描述事件发生的时间间隔，比如电子元件的寿命、顾客到来的间隔时间等。
- t分布：用于小样本数据分析，常用于估计均值的置信区间，特别是在样本量小于30时。

## 2.2 常见概率分布类型

### 2.2.1 离散型概率分布

离散型概率分布是概率论和统计学中应用非常广泛的一类分布，其最核心的特点是取值为离散值。

#### 二项分布

二项分布是离散型概率分布中的一个基础类型，由两个参数n和p定义：

- n：试验次数
- p：每次试验的成功概率

对于任意整数k（0 ≤ k ≤ n），二项分布的概率质量函数是：

def binom_pmf(k, n, p):
    return comb(n, k) * (p**k) * ((1-p)**(n-k))

其中`comb(n, k)`是组合数，表示从n个不同元素中取出k个元素的组合数。

二项分布的图形通常呈现出钟形，随着n的增加，其形状趋于对称。在实际应用中，二项分布通常用于统计诸如抛硬币试验中出现正面的次数等。

#### 泊松分布

泊松分布在概率论和统计学中也非常常见，它通常用来描述在固定时间或空间间隔内随机事件发生的次数。

泊松分布由参数λ（事件发生率）定义，其概率质量函数为：

def poisson_pmf(k, lmbda):
    return (lmbda**k * exp(-lmbda)) / factorial(k)

其中`exp`是自然指数函数，`factorial(k)`是k的阶乘。

泊松分布的图形通常呈现出偏斜的形态，随着λ的增加，分布形态趋于对称。泊松分布广泛用于模拟电话呼叫、交通事故发生次数等。

### 2.2.2 连续型概率分布

连续型概率分布与离散型不同，它描述的是连续的随机变量，如人的身高、物体的重量等。

#### 正态分布

正态分布，也被称为高斯分布，是连续型概率分布中最重要的一种，广泛应用于自然科学和社会科学领域。

正态分布的概率密度函数为：

def normal_pdf(x, mu, sigma):
    return (1 / (sigma * sqrt(2 * pi))) * exp(-0.5 * ((x - mu) / sigma)**2)

其中μ（mu）是均值，σ（sigma）是标准差。正态分布图形呈现出对称的钟形，其均值、中位数和众数是相同的。

在实际应用中，正态分布在质量控制、数据分析、信号处理等领域中占据着核心地位，因为很多自然现象和社会现象的测量数据都呈现出正态分布的特点。

#### 指数分布

指数分布是描述独立随机事件发生的时间间隔的概率分布，经常用于寿命分析、排队理论等领域。

其概率密度函数为：

def exponential_pdf(x, lmbda):
    return lmbda * exp(-lmbda * x) if x >= 0 else 0

其中λ（lmbda）是单位时间（或单位空间）内发生事件的平均次数（或平均频率）。指数分布的图形通常向右倾斜。

由于指数分布的特点，它在诸如故障分析、服务时间预测等领域有着广泛的应用。

## 2.3 概率分布的数学性质

### 2.3.1 均值、方差与标准差

均值、方差和标准差是描述随机变量分布特性的基本数学指标。

- 均值（期望值）：反映了随机变量的集中趋势，是随机变量所有可能取值的加权平均。
- 方差：衡量了随机变量取值的离散程度，即各数据点与均值差异的平方的平均数。
- 标准差：方差的平方根，对数据的离散程度提供了直观的度量。

### 2.3.2 概率质量函数与概率密度函数

对于离散型随机变量，其概率分布通过概率质量函数（Probability Mass Function, PMF）来描述，而连续型随机变量则通过概率密度函数（Probability Density Function, PDF）来描述。

- 概率质量函数（PMF）：对于离散型随机变量X，函数f(x) = P(X=x)称为概率质量函数。
- 概率密度函数（PDF）：对于连续型随机变量X，函数f(x)满足P(a ≤ X ≤ b) = ∫[a,b] f(x)dx，称为概率密度函数。

概率密度函数与概率质量函数的图像提供了直观的概率分布图景，它们是概率分布分析中的重要工具。在统计分析、机器学习等领域，概率分布的理论知识是构建模型和推断参数的基础。

# 3. Python中的绘图库

## 3.1 Matplotlib绘图基础

### 3.1.1 Matplotlib简介

Matplotlib是Python中最流行的绘图库之一，它提供了一个强大的绘图框架，使得用户能够创建各种静态、动态、交互式的图表。作为一个2D绘图库，Matplotlib允许用户自定义各种图表的细节，如线条样式、颜色、坐标轴刻度等。尽管Matplotlib在功能上可能不及一些新兴的绘图库（比如Seaborn），但它强大的基础和广泛的应用使其成为学习Python绘图的入门必选。

Matplotlib的主要模块是`matplotlib.pyplot`，它提供了一个类似于MATLAB的绘图环境。通过这个模块，用户可以快速创建图表，并进行简单的定制。Matplotlib支持多种输出格式，如PNG、JPG、SVG等，这使得创建的图表可以轻松地嵌入到文档、网页和报告中。

### 3.1.2 创建基础图表

创建一个基础图表非常简单，只需要几个步骤。首先，导入`matplotlib.pyplot`模块，然后使用`plot`函数进行绘图，并用`show`函数显示图表。下面是一个简单的示例：

import matplotlib.pyplot as plt

# 准备数据
x = [0, 1, 2, 3, 4, 5]
y = [0, 1, 4, 9, 16, 25]

# 绘制线图
plt.plot(x, y)

# 显示图表
plt.show()

这段代码将会输出一个简单的线图，展示函数`f(x)=x^2`的图像。这个例子虽然简单，但展示了使用Matplotlib绘图的基本流程。

为了进一步定制图表，可以使用更多`matplotlib.pyplot`中的函数，例如设置图表标题、轴标签、图例等：

# 设置图表标题和轴标签
plt.title("Square function plot")
plt.xlabel("x axis")
plt.ylabel("y axis")

# 添加图例
plt.legend(["f(x) = x^2"])

### 3.1.3 细节定制

Matplotlib的功能不仅限于创建基本图表。它还提供了丰富的API用于定制图表的细节，例如颜色、线型、标记样式等。这些定制可以让图表更符合特定的展示需求。

例如，可以改变线条的颜色和宽度：

plt.plot(x, y, color="red", linewidth=2.0)

或者添加数据点的标记，以及改变标记的样式：

plt.plot(x, y, marker="o", markersize=6)

通过这些方法，可以调整图表的外观，使其更加美观和专业。Matplotlib的灵活性使其适用于从简单的数据分析到复杂的科研图表的创建。

### 3.1.4 图表类型

Matplotlib支持多种类型的图表，从基础的线图、柱状图到三维图和地图等。用户可以通过不同的绘图函数来创建不同类型的图表，例如`plt.bar`用于柱状图，`plt.scatter`用于散点图，`plt.hist`用于直方图等。

这些图表可以被用来展示数据的分布、关系和趋势。例如，直方图可以清晰地显示出数据集的频率分布情况，而散点图则非常适合展示两个变量之间的相关性。

## 3.2 Seaborn的高级绘图功能

### 3.2.1 Seaborn与Matplotlib的关系

Seaborn是一个基于Matplotlib的高级绘图库，它提供了更为简洁和美观的API来创建统计图表。Seaborn的设计目的是让绘图更加简单和直观，尤其是在处理统计图表时。

由于Seaborn是构建在Matplotlib之上的，因此它保留了Matplotlib的许多功能，同时引入了更为复杂和高级的图表类型，如箱形图、热图、小提琴图等。Seaborn通过预设的主题和调色板简化了图表的定制过程，使得创建具有吸引力的统计图表变得容易。

### 3.2.2 Seaborn的统计数据可视化

Seaborn的统计数据可视化功能十分强大，它内置了多种用于统计分析和数据可视化的函数。通过Seaborn，可以非常方便地创建分组图表、配对图、回归图等。这些图表在数据探索和解释时非常有用，尤其是在处理大型数据集时。

例如，`sns.boxplot`函数可以用来创建箱形图，箱形图可以展示数据的中位数、四分位数以及异常值：

import seaborn as sns
import pandas as pd

# 准备数据
tips = sns.load_dataset("tips")

# 创建箱形图
sns.boxplot(x="day", y="total_bill", data=tips)

这个例子中，箱形图展示了在不同天的总账单分布情况，包括中位数、四分位数以及可能的异常值。

Seaborn也支持创建热图，热图是一种很好的展示大规模数据矩阵的方法。例如，它可以用来展示矩阵数据的分布情况或者两个变量之间的相关性：

# 创建热图
corr = tips.corr()
sns.heatmap(corr, annot=True, cmap="coolwarm")

在这个例子中，热图通过不同颜色的深浅展示了数据集中各变量间的相关系数。

## 3.3 其他绘图库简介

### 3.3.1 Plotly的交互式图表

Plotly是一个用于创建交互式图表的库。与Matplotlib和Seaborn不同，Plotly生成的图表可以嵌入到网页中，并通过JavaScript与图表进行交云互动。Plotly支持各种类型的图表，并且可以通过Plotly的在线平台免费托管图表。

Plotly的一个显著特点是它的交互性，例如缩放、拖动、悬停提示等，使得图表的数据分析更加直观和方便。Plotly也支持创建3D图表，这在很多领域都有应用。

### 3.3.2 Bokeh的动态图表

Bokeh是一个Python库，用于生成具有复杂图形和交互性的现代Web应用程序。与Plotly类似，Bokeh也专注于创建交互式的图表，并能够生成高质量的静态图形用于出版。

Bokeh提供了灵活的图表布局和美观的图表定制选项，其图表可以在现代Web浏览器中查看。Bokeh的图表可以用来创建各种交互式小部件，如滑动条、选择框等，这些小部件可以和图表元素联动，从而允许用户在图表上直接进行查询和过滤操作。

Bokeh同样支持集成到Web应用程序中，它提供了一套丰富的API来构建和部署复杂的Web可视化应用。

以上介绍了Python中常用的几个绘图库。在接下来的章节中，我们将深入探讨如何使用这些库来绘制特定的概率分布图。

# 4. 离散型概率分布图绘制

在本章节中，我们将深入探讨如何使用Python来绘制常见的离散型概率分布图。离散型概率分布是统计学和概率论中非常重要的部分，它们描述了随机变量取特定离散值的概率。本章节将重点介绍三种常见的离散型概率分布：二项分布、泊松分布和几何分布，并通过实际代码案例展示如何利用Python中的库来绘制这些分布图。

## 4.1 二项分布图

二项分布是离散概率分布中的一种，常用于描述在固定次数的独立实验中，成功次数的概率分布情况，其中每次实验的成功概率是相同的。

### 4.1.1 二项分布的理论基础

二项分布由两个参数定义：试验次数n和每次试验成功的概率p。其概率质量函数（PMF）可以表示为：

\[ P(X=k) = C(n,k) \cdot p^k \cdot (1-p)^{n-k} \]

其中，\(C(n,k)\)是组合数，表示从n个不同元素中选取k个元素的组合数，\(P(X=k)\)是恰好取得k次成功的概率。

### 4.1.2 Python实现二项分布图绘制

为了绘制二项分布图，我们可以使用Python中的`matplotlib`和`scipy`库。首先，我们需要安装这些库（如果尚未安装）：

pip install matplotlib scipy

接下来是绘制二项分布图的Python代码：

import matplotlib.pyplot as plt
from scipy.stats import binom
import numpy as np

# 设定二项分布的参数
n = 10  # 实验次数
p = 0.5  # 每次实验成功的概率

# 生成二项分布数据
rv = binom(n, p)
x = np.arange(0, n+1)
pmf = rv.pmf(x)

# 绘制概率质量函数图
plt.figure(figsize=(10, 5))
plt.bar(x, pmf)
plt.title('Binomial Distribution PMF')
plt.xlabel('Number of Successes')
plt.ylabel('Probability')
plt.grid(True)
plt.show()

在上述代码中，我们首先导入了必要的库，并设置了二项分布的参数：实验次数为10次，每次实验成功的概率为0.5。然后，我们使用`scipy.stats.binom`定义了一个二项分布，并生成了一个包含从0到n的所有可能成功次数的概率质量函数值。最后，我们使用`matplotlib.pyplot`库绘制了二项分布的概率质量函数图。

## 4.2 泊松分布图

泊松分布是描述在固定时间或空间内，发生某事件的次数的概率分布。

### 4.2.1 泊松分布的特点和应用场景

泊松分布由参数λ（事件的平均发生率）来定义。其概率质量函数表示为：

\[ P(X=k) = \frac{e^{-\lambda} \lambda^k}{k!} \]

泊松分布通常用于模拟在固定时间或空间内随机事件发生的次数，如电话呼叫中心在一个小时内接到的电话数量等。

### 4.2.2 Python实现泊松分布图绘制

绘制泊松分布图同样需要导入`matplotlib.pyplot`和`scipy.stats`库：

import matplotlib.pyplot as plt
from scipy.stats import poisson
import numpy as np

# 设定泊松分布的参数
lam = 5  # 事件的平均发生率

# 生成泊松分布数据
rv = poisson(lam)
x = np.arange(0, 20)  # 定义一个范围内可能的事件发生次数
pmf = rv.pmf(x)

# 绘制概率质量函数图
plt.figure(figsize=(10, 5))
plt.bar(x, pmf)
plt.title('Poisson Distribution PMF')
plt.xlabel('Number of Occurrences')
plt.ylabel('Probability')
plt.grid(True)
plt.show()

在这段代码中，我们使用`scipy.stats.poisson`定义了泊松分布，并生成了一个包含从0到20的可能事件发生次数的概率质量函数值。我们利用`matplotlib.pyplot`绘制了这些数据点，生成了泊松分布的概率质量函数图。

## 4.3 几何分布图

几何分布用来描述在一系列独立的伯努利试验中，试验成功之前的失败次数的概率分布。

### 4.3.1 几何分布的概率解释

几何分布的概率质量函数定义为：

\[ P(X=k) = (1-p)^k \cdot p \]

其中，p是每次试验成功的概率，而k表示失败的次数。

### 4.3.2 Python实现几何分布图绘制

绘制几何分布图的Python代码如下：

import matplotlib.pyplot as plt
from scipy.stats import geom
import numpy as np

# 设定几何分布的参数
p = 0.3  # 每次实验成功的概率

# 生成几何分布数据
rv = geom(p)
x = np.arange(0, 15)  # 定义一个范围内可能的失败次数
pmf = rv.pmf(x)

# 绘制概率质量函数图
plt.figure(figsize=(10, 5))
plt.bar(x, pmf)
plt.title('Geometric Distribution PMF')
plt.xlabel('Number of Failures Before First Success')
plt.ylabel('Probability')
plt.grid(True)
plt.show()

在上述代码中，我们使用`scipy.stats.geom`定义了几何分布，并生成了一个包含从0到15的可能失败次数的概率质量函数值。通过`matplotlib.pyplot`库，我们绘制了这些数据点，得到了几何分布的概率质量函数图。

通过本章节的介绍，我们可以看到在Python环境中使用`matplotlib`和`scipy.stats`库进行离散型概率分布图绘制是十分方便且直观的。在下一节中，我们将继续探讨连续型概率分布图的绘制方法。

# 5. 连续型概率分布图绘制

## 5.1 正态分布图
正态分布，又称为高斯分布，是自然界和社会科学领域中最为常见的一种连续型概率分布。它在统计学、机器学习、信号处理等领域有着广泛的应用。本节将详细介绍正态分布的性质，以及如何使用Python来绘制正态分布的概率分布图。

### 5.1.1 正态分布的性质和重要性
正态分布的概率密度函数具有对称的钟形曲线形状，其均值、中位数、众数三者相等，是最典型的对称分布。它有两个参数：均值μ和标准差σ，分别决定分布的中心位置和分布的宽窄。正态分布具有以下重要性质：

- 曲线关于均值μ对称。
- 曲线在均值μ处达到最高点，且随着距离均值越远，曲线高度递减。
- 曲线与x轴之间围成的面积恒等于1。
- 当数据服从正态分布时，根据中心极限定理，大量独立随机变量的和或平均值，也将趋近于正态分布。

由于这些性质，正态分布成为了描述自然和社会现象的重要数学模型，例如，测量误差、学生的考试成绩、人类的身高体重等。

### 5.1.2 Python实现正态分布图绘制
使用Python中的`matplotlib`和`numpy`库，可以非常方便地绘制正态分布的概率分布图。以下是代码示例：

import numpy as np
import matplotlib.pyplot as plt

# 设定正态分布的参数
mu = 0   # 均值
sigma = 1 # 标准差

# 创建x轴的数据点
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 100)
# 计算对应的正态分布概率密度函数值
y = (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu)/sigma) ** 2)

# 绘制正态分布曲线
plt.plot(x, y, label='Normal Distribution mu={0}, sigma={1}'.format(mu, sigma))
plt.title('Normal Distribution')
plt.xlabel('X axis')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

上面的代码首先导入了必要的库，然后设置了正态分布的参数，并生成了一系列x轴上的数据点。接着计算了每个点对应的概率密度值，最后将它们绘制在图表上。通过调整`mu`和`sigma`的值，你可以绘制出不同均值和标准差的正态分布图。

### 正态分布图的深入理解
绘制正态分布图不仅仅是为了一张美观的图形，更重要的是要理解其背后的数学意义和统计性质。正态分布图提供了一种直观的方法来分析数据的分布特征。例如，可以大致判断数据分布的中心位置以及数据的离散程度。在机器学习中，正态分布常常用于初始化模型参数、处理缺失值以及异常值检测等场景。

### 正态分布图的扩展应用
在实际应用中，正态分布图常常与其他统计工具结合使用，例如假设检验、置信区间的计算等。例如，当数据量足够大时，根据中心极限定理，我们可以使用正态分布对样本均值的分布进行近似，进一步进行统计推断。

### 正态分布图与其他概率分布的比较
在研究概率分布时，除了正态分布外，还会有许多其他类型的连续概率分布，如均匀分布、指数分布等。通过绘制这些分布的概率分布图，我们可以直观比较它们之间的差异，如分布的形态、尾部的厚薄等。这对于选择合适的数据分布模型具有重要的参考价值。

## 5.2 指数分布图
指数分布是在许多物理、工程、社会科学问题中常见的连续型概率分布。它主要描述了两个连续事件发生之间的时间间隔。本节将讨论指数分布的理论基础，并展示如何用Python绘制指数分布图。

### 5.2.1 指数分布的理论基础
指数分布的概率密度函数为：

\[ f(x;\lambda) = \begin{cases}
\lambda e^{-\lambda x} & \text{for } x \geq 0, \\
0 & \text{for } x < 0.
\end{cases} \]

其中，λ > 0 是分布的率参数（rate parameter），决定了分布曲线下降的速度。当λ增加时，曲线下降得更快。指数分布有一个重要的性质，即无记忆性（memorylessness），这意味着未来发生的事件不受过去发生事件的影响。

### 5.2.2 Python实现指数分布图绘制
为了绘制指数分布图，我们可以使用`numpy`来生成样本数据，并使用`matplotlib`来进行绘图。下面是一个Python代码示例：

import numpy as np
import matplotlib.pyplot as plt

# 设置指数分布的参数
rate = 1.0 # λ为1

# 生成指数分布的样本数据
samples = np.random.exponential(scale=1/rate, size=1000)
samples.sort()

# 绘制直方图表示样本的概率密度
plt.hist(samples, density=True, bins=30, alpha=0.6, color='g')

# 绘制指数分布的理论概率密度函数
x = np.linspace(0, 10, 100)
y = rate * np.exp(-rate * x)
plt.plot(x, y, 'k', linewidth=2)

plt.title('Exponential Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.grid(True)
plt.show()

在这段代码中，我们首先定义了指数分布的率参数`rate`。然后，我们使用`np.random.exponential`函数生成了1000个指数分布的随机样本，并对其进行了排序。接着，我们通过`plt.hist`函数绘制了样本数据的直方图，并将`density`参数设置为`True`以显示概率密度。最后，我们计算并绘制了指数分布的理论概率密度函数。

### 指数分布图的意义与应用
指数分布图在各种领域中都有广泛的应用，特别是在可靠性工程中，指数分布常用来描述设备的寿命或故障间隔时间。此外，指数分布也是无记忆队列模型、泊松过程等模型的基础。

### 指数分布图的扩展应用
在实际问题中，当我们知道一个事件发生的平均时间间隔时，可以使用指数分布来模拟事件的发生过程。在数据科学中，指数分布可以用于时间序列分析，特别是在分析顾客到达、网页点击等时间间隔问题上。

## 5.3 t分布图
t分布是统计学中另一种常见的连续型概率分布，特别在小样本数据分析中占有重要的地位。本节将探讨t分布的定义、特点，并演示如何在Python中实现t分布图。

### 5.3.1 t分布的定义和特点
t分布由威廉·戈塞特（William Sealy Gosset）在1908年提出，主要用于小样本数据集的统计分析。t分布的概率密度函数比正态分布的尾部更重，即其尾部下降得更缓慢，这使得t分布更适合描述小样本数据的统计特征。t分布的概率密度函数为：

\[ f(x; \nu) = \frac{\Gamma(\frac{\nu+1}{2})}{\sqrt{\nu\pi}\Gamma(\frac{\nu}{2})}\left(1+\frac{x^2}{\nu}\right)^{-\frac{\nu+1}{2}} \]

其中，\(\nu\) 是自由度参数，决定了t分布的形状；\(\Gamma\) 是伽马函数。随着自由度的增加，t分布逐渐接近正态分布。

### 5.3.2 Python实现t分布图绘制
绘制t分布图可以使用`scipy.stats`模块中的`t`类。下面是一个绘制t分布概率密度函数图的示例：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t

# 设定自由度参数
degrees_of_freedom = 10

# 创建x轴的数据点
x = np.linspace(-5, 5, 100)
# 计算对应的t分布概率密度函数值
y = t.pdf(x, degrees_of_freedom)

# 绘制t分布曲线
plt.plot(x, y, label='t Distribution df={}'.format(degrees_of_freedom))
plt.title('t Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

在这段代码中，我们首先导入了必要的库，然后定义了自由度`degrees_of_freedom`。之后，我们生成了一系列x轴上的数据点，并计算了每个点对应的t分布概率密度值。最后，我们将这些值绘制在图表上。

### t分布图的深入应用
t分布图不仅展示了t分布的形状，还可以用于理解t检验的工作原理。在小样本数据集的均值差异性检验中，t分布提供了一种有效的统计方法来确定数据的显著性水平。

### t分布图的扩展应用
在数据分析中，t分布图可用于计算置信区间和假设检验。例如，在进行t检验时，t分布图可以帮助我们确定样本均值与总体均值差异的统计意义，进而做出合理的推断。此外，t分布也是贝叶斯分析中的一部分，特别是在贝叶斯推断中，t分布被用作先验分布。

# 6. 概率分布图的综合应用

## 6.1 数据分布的探索性分析

在数据分析的初期阶段，了解数据的分布特性是至关重要的。通过概率分布图，我们可以直观地理解数据的集中趋势、分散程度以及数据的形状。

### 6.1.1 数据分布的基本判断方法

数据分布的基本判断方法通常包括：

- **中心位置**：通过均值、中位数和众数来判断数据分布的中心位置。
- **离散程度**：方差、标准差和四分位数范围可以用来衡量数据的离散程度。
- **偏态和峰态**：偏态系数可以判断分布的对称性，峰态系数可以反映分布的尖峭或平坦程度。

### 6.1.2 利用概率分布图进行数据分析

概率分布图，如直方图、箱形图、Q-Q图等，是探索性数据分析的重要工具：

- **直方图**：直观地展示了数据的频率分布情况。
- **箱形图**：提供了关于数据分布的五数概括（最小值、第一四分位数、中位数、第三四分位数和最大值）。
- **Q-Q图**：用于比较两个概率分布是否相似。

## 6.2 概率分布图在机器学习中的应用

在机器学习领域，概率分布图不仅用于数据预处理阶段，也广泛应用于模型评估和算法优化等环节。

### 6.2.1 概率分布图在模型评估中的作用

模型评估阶段使用概率分布图：

- **残差分析**：残差图用于判断回归模型的准确性。
- **ROC曲线**：在分类模型中，ROC曲线展示模型的真正类率与假正类率的关系。

### 6.2.2 概率分布图在决策树等算法中的应用

在算法选择和优化过程中，概率分布图可以帮助我们：

- **特征选择**：依据特征的概率分布选择最有信息量的特征。
- **模型比较**：通过比较不同模型的输出分布来评估模型的有效性。

## 6.3 实战案例分析

为了更好地理解概率分布图在实际工作中的应用，让我们通过一个实战案例来进行分析。

### 6.3.1 实际案例选取

选取一个常见的业务场景，比如客户流失预测，来展示如何通过概率分布图进行数据分析和决策支持。

### 6.3.2 数据预处理和分布图绘制过程

在数据预处理阶段，我们将数据集分为训练集和测试集。接下来，绘制各特征的分布图以进行初步分析：

import matplotlib.pyplot as plt
import pandas as pd

# 加载数据集
data = pd.read_csv('customer_churn.csv')

# 数据预处理（省略具体代码）

# 绘制直方图
data.hist(bins=20, figsize=(15, 10))
plt.show()

# 绘制箱形图
data.boxplot(column=['Feature1', 'Feature2', 'Feature3'])
plt.show()

### 6.3.3 案例解读与结论

通过分析直方图和箱形图，我们可以发现某些特征的分布情况。例如，特征1可能显示出明显的偏态，这可能表明需要对数据进行转换，或者在模型中考虑非线性关系。

通过这个实战案例，我们可以看到概率分布图不仅帮助我们识别数据中的模式和异常值，而且为模型的选择和优化提供了依据。在实际应用中，这种分析是推动业务发展和改进的重要一环。