数据分析中的概率分布应用：概率分布的现实应用指南

# 1. 概率分布基础概述

## 1.1 概率分布的意义与应用

概率分布是统计学和概率论中的核心概念，它描述了随机变量取各种可能值的概率。在数据分析、机器学习、金融分析等领域中，概率分布帮助我们理解数据的生成机制和特征。例如，在质量控制中，通过了解产品尺寸的概率分布，可以有效地进行过程控制和改进。

## 1.2 随机变量与概率分布函数

随机变量是取值受随机现象影响的变量，其每一个可能的结果对应一个数值。概率分布函数（Probability Distribution Function，PDF）用于描述离散型随机变量的概率分布，而概率密度函数（Probability Density Function，PDF）则描述连续型随机变量的概率分布情况。理解这两种函数对于分析和处理问题至关重要。

## 1.3 概率分布的表示方法

概率分布可以通过多种方式来表示，包括图形化（如直方图、概率密度曲线）、数值化（如概率表、概率质量函数）以及公式化（如分布的数学表达式）。每种表示方法都有其适用场景，比如在理论研究中常使用数学表达式，而在实际应用中，则更多使用图形化和数值化方法以直观地展示数据特征。

本章介绍了概率分布的基本概念和应用，并强调了随机变量在描述概率分布中的角色。接下来的章节将深入探讨概率分布背后的数学原理和在各种专业领域中的具体应用。

# 2. 概率分布的数学原理

## 2.1 基本概念与定义

### 2.1.1 随机变量与概率分布函数

随机变量是概率论和统计学中的核心概念，它是一个可以取不同值的变量，其结果的出现是不确定的。在概率论中，随机变量通常用大写字母（如X、Y或Z）表示，其可能取的值用小写字母（如x、y或z）表示。随机变量可以是离散的也可以是连续的。

概率分布函数（Probability Distribution Function, PDF）或累积分布函数（Cumulative Distribution Function, CDF）是描述随机变量取值概率的函数。对于连续型随机变量X，PDF是指定X取特定值的概率密度函数f(x)，通过积分得到概率：
\[ P(a \leq X \leq b) = \int_{a}^{b} f(x) \, dx \]

对于离散型随机变量X，概率分布则是通过概率质量函数（Probability Mass Function, PMF）来描述，记为p(x)，它表示X取某一特定值x的概率：
\[ P(X = x) = p(x) \]

### 2.1.2 概率质量函数与概率密度函数

概率质量函数（PMF）适用于离散型随机变量，它显示了每个可能结果发生的概率。PMF的数学形式是：
\[ p(x) = P(X = x) \]

概率密度函数（PDF）适用于连续型随机变量，表示随机变量在某个确定区间内取值的概率。PDF需满足两个条件：
\[ f(x) \geq 0 \quad \text{且} \quad \int_{-\infty}^{\infty} f(x) \, dx = 1 \]

PDF本身不是一个概率，而是一个密度，其积分给出了随机变量在给定区间内的概率。

## 2.2 常见的概率分布类型

### 2.2.1 离散型分布：二项分布、泊松分布

二项分布是离散型随机变量的一个常见分布类型，常用于描述固定次数的独立实验中成功次数的概率分布，其中每次实验成功的概率是固定的。二项分布的概率质量函数为：
\[ p(x) = \binom{n}{x} p^x (1-p)^{n-x} \]
其中 \( \binom{n}{x} \) 是组合数，表示从n次实验中选择x次成功的方式数，\( p \) 是单次实验成功的概率。

泊松分布用于描述在一定时间或空间内发生某事件的次数的概率分布，适合用于描述稀有事件。泊松分布的概率质量函数为：
\[ p(x) = \frac{\lambda^x e^{-\lambda}}{x!} \]
其中 \( \lambda \) 是单位时间或空间内平均事件发生的次数，\( e \) 是自然对数的底数。

### 2.2.2 连续型分布：正态分布、指数分布

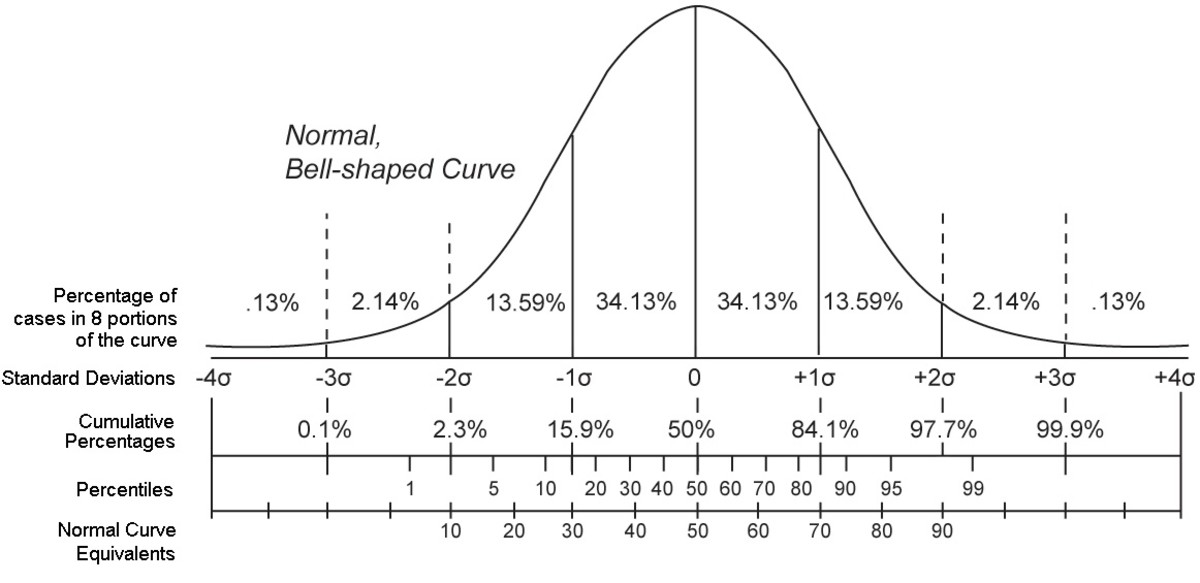
正态分布是连续型随机变量中最常见的分布之一，又称为高斯分布，广泛应用于自然科学和社会科学中。正态分布的概率密度函数为：
\[ f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]
其中，\( \mu \) 是分布的均值，\( \sigma \) 是标准差。

指数分布常用于描述两个连续独立事件发生之间的时间间隔。其概率密度函数为：
\[ f(x) = \lambda e^{-\lambda x} \]
其中，\( \lambda \) 是平均发生率（即单位时间内发生次数的倒数）。

## 2.3 概率分布的性质与参数估计

### 2.3.1 分布的期望值、方差和标准差

期望值、方差和标准差是衡量概率分布特征的几个重要参数。期望值（均值）是概率分布的平均或中心值，定义为：
\[ E(X) = \mu = \begin{cases} \sum x p(x) & \text{对于离散型} \\ \int_{-\infty}^{\infty} x f(x) dx & \text{对于连续型} \end{cases} \]

方差衡量的是随机变量的离散程度，定义为：
\[ \text{Var}(X) = \sigma^2 = E[(X - \mu)^2] \]

标准差是方差的平方根，它是衡量数据分散程度的度量。

### 2.3.2 参数估计方法：最大似然估计、矩估计

参数估计是根据样本数据来推断总体参数的过程。最大似然估计（MLE）和矩估计是两种常见的估计方法。

最大似然估计是选择参数使得观测到的数据出现的概率最大。其数学表示为：
\[ \hat{\theta}_{MLE} = \arg \max_{\theta} \prod_{i=1}^{n} f(x_i | \theta) \]

矩估计方法是利用样本矩与总体矩相等的原理来估计总体参数。对于第一个矩（均值）和第二个矩（方差）