概率分布与假设检验：构建统计模型的坚实基石

# 1. 概率分布与假设检验的基本概念

在统计学和数据分析中，概率分布是理解随机变量行为的基础，而假设检验是推断统计中不可或缺的一部分。本章将为我们揭开这两个概念的神秘面纱，并介绍它们在现代IT和数据科学领域中的应用。

概率分布描述了随机变量可能取值的概率。简单来说，它可以告诉我们在给定条件下某个事件发生的可能性有多大。比如，如果我们抛一次硬币，硬币出现正面的概率是0.5。

假设检验则是用来基于样本数据对总体参数作出推断的一种统计方法。它通常涉及设定一个原假设（null hypothesis），该假设通常表示无效应或者状态不变，然后收集数据并计算统计量以确定是否拒绝原假设。比如，检验一个新开发的软件功能是否真的比旧功能更快。

在接下来的章节中，我们会进一步深入到各种概率分布和假设检验的细节中，从而为读者提供在实际工作中应用这些工具的能力。

# 2. 离散型随机变量的概率分布

### 2.1 离散概率分布的理论基础

#### 2.1.1 概率质量函数的定义与性质

概率质量函数（Probability Mass Function，简称 PMF）是离散型随机变量的数学描述，它为每一个可能的离散结果指定了一个概率值。这些概率值满足以下性质：

- 对于离散随机变量的所有可能结果 \(x_i\)，其概率质量函数值 \(P(X = x_i)\) 均大于或等于零。
- 概率值之和等于一，即 \(\sum_{i} P(X = x_i) = 1\)。
- 可以通过PMF计算随机变量取特定值的概率，也可以用于求解随机变量的期望值和方差等其他特征。

#### 2.1.2 常见的离散概率分布

在众多离散概率分布中，二项分布、泊松分布、超几何分布是三种基础且广泛应用于各种场景的分布。

- **二项分布**：当一个随机过程只有两个结果（成功或失败），且重复进行n次独立实验时，实验成功的次数就遵循二项分布。
- **泊松分布**：用于描述在固定时间或空间内发生某事件的次数，该事件发生的概率与间隔时间成正比，与间隔数量成反比。
- **超几何分布**：适用于无放回的抽取，例如在没有替换的情况下从有限的集合中抽取样本。

### 2.2 离散型随机变量的实践应用

#### 2.2.1 二项分布及其实际案例分析

二项分布是统计学中一个非常重要的概率分布，它描述了固定次数的独立实验中成功次数的概率分布。例如，在10次抛硬币的实验中，我们关心的是“恰好出现4次正面”的概率。

通过二项分布公式 \(P(X = k) = \binom{n}{k}p^k(1-p)^{n-k}\)，我们可以计算出在n次独立伯努利实验中成功k次的概率，其中 \(\binom{n}{k}\) 表示组合数，\(p\) 表示单次实验成功的概率。

下面通过一个Python代码示例来展示如何使用二项分布计算上述硬币投掷问题的概率：

import scipy.stats as stats

# 设定实验参数
n = 10  # 实验次数
p = 0.5  # 硬币正面朝上的概率
k = 4  # 成功次数（正面出现次数）

# 计算恰好出现4次正面的概率
probability = stats.binom.pmf(k, n, p)
print(f"恰好出现 {k} 次正面的概率为: {probability}")

#### 2.2.2 泊松分布在事件计数中的应用

泊松分布在处理“计算在给定时间内或给定区域内发生某一随机事件的次数”这类问题中非常有用。假设我们想计算在1小时内，平均有5辆汽车通过的路口，在2小时内恰好有7辆汽车通过的概率。

泊松分布的概率质量函数为 \(P(X = k) = \frac{e^{-\lambda}\lambda^k}{k!}\)，其中 \(\lambda\) 为单位时间或单位区域内的平均事件数。

下面是一个使用Python来计算泊松分布概率的代码示例：

# 设定参数
lambda_ = 10  # 单位时间内平均事件数（例如汽车通过次数）
k = 7  # 某段时间内的实际事件数

# 计算概率
probability = stats.poisson.pmf(k, lambda_)
print(f"在单位时间内恰好有 {k} 辆汽车通过的概率为: {probability}")

#### 2.2.3 超几何分布与其他离散分布的对比

超几何分布在没有替换的抽样问题中有广泛的应用，例如在抽奖活动中，抽取一定数量的奖品中奖率的计算。与二项分布和泊松分布相比，超几何分布的一个关键特性是在每次抽取中事件发生的概率不是独立的。

超几何分布的概率质量函数为 \(P(X = k) = \frac{\binom{K}{k}\binom{N-K}{n-k}}{\binom{N}{n}}\)，其中 \(N\) 是总数，\(K\) 是其中有标记的元素数量，\(n\) 是抽取的元素数量，\(k\) 是其中标记的元素数量。

通过对比这三种分布的公式和应用场景，我们可以更深入地理解每种分布的适用条件和区别。例如，如果某事件的发生在每次尝试中是独立的，那么应优先选择二项分布或泊松分布；如果事件发生不独立，或是在有限总体中无放回抽样，则超几何分布更为合适。

# 3. 连续型随机变量的概率分布

## 3.1 连续概率分布的理论基础

### 3.1.1 概率密度函数的定义与性质

在连续型随机变量的领域中，概率密度函数（Probability Density Function, PDF）扮演着至关重要的角色。与离散型随机变量的概率质量函数（Probability Mass Function, PMF）不同，概率密度函数描述的是一个随机变量取值在某区间内的概率。这意味着连续随机变量取任一特定值的概率实际上为零，但其在某个区间内取值的概率却可以是正的。

概率密度函数需满足以下性质：
- 非负性：f(x) ≥ 0 对于所有x。
- 归一性：∫ f(x) dx = 1，积分在整个定义域内进行，确保随机变量取任意值的总概率为1。
- 连续变量X落在区间 [a, b] 内的概率等于该区间的概率密度函数下的面积，即 P(a ≤ X ≤ b) = ∫(从a到b) f(x) dx。

理解这些性质是深入探讨连续型随机变量概率分布的关键，它们构成了连续型随机变量理论分析的基础。

### 3.1.2 常见的连续概率分布

在统计学和数据分析中，几种典型的连续概率分布经常被提及和使用：

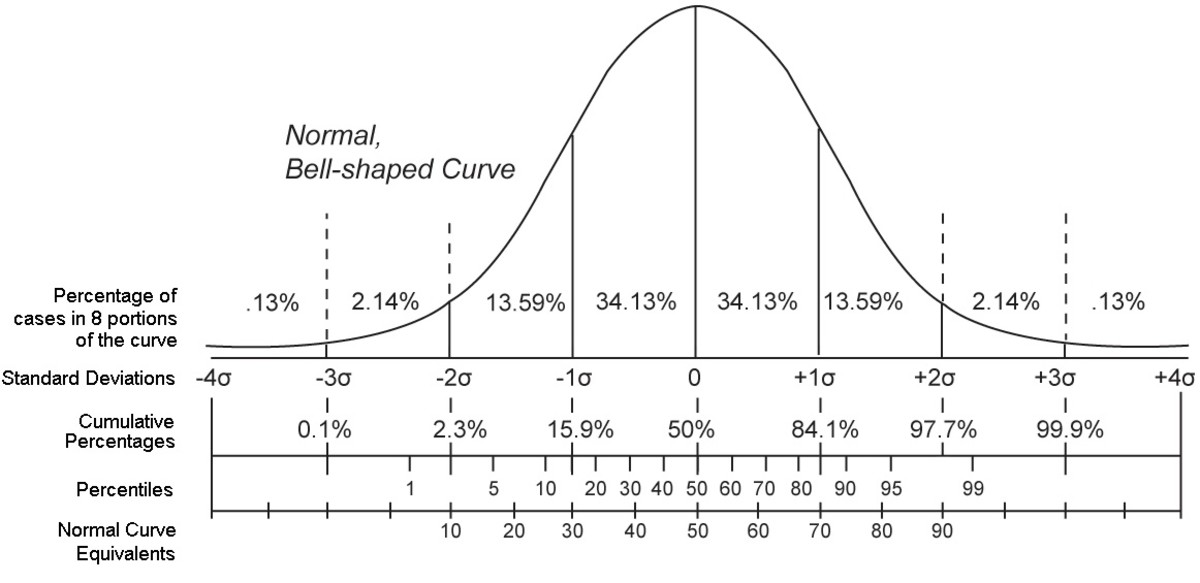
- **正态分布**：是最常见的连续概率分布，其概率密度函数呈钟形曲线。正态分布由两个参数μ（均值）和σ²（方差）决定。
- **指数分布**：常用来描述两个连续事件发生之间的时间间隔，如电子设备的寿命。指数分布只有