响应曲面方法在产品研发中的应用：如何提高产品设计质量


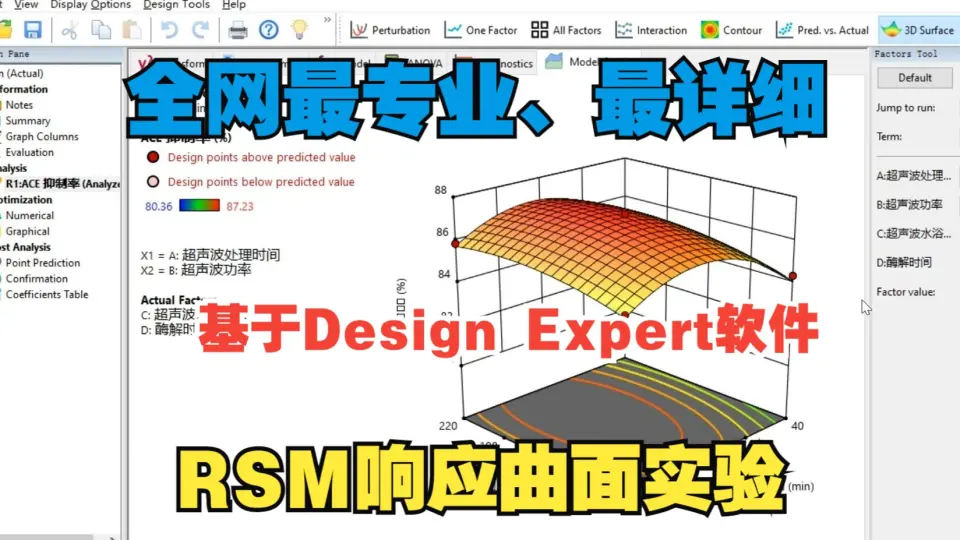
# 摘要
响应曲面方法（Response Surface Methodology, RSM）是一种结合统计学和数学方法的技术，用于分析影响过程的变量和优化过程性能。本文首先介绍RSM的基本概念及其理论基础，包括统计实验设计原理、数学模型的建立与优化策略。接着，文中深入探讨了RSM在产品研发中的实践应用，涵盖了实验设计的实施流程、响应曲面的建立与分析，以及产品设计优化案例分析。此外，本文还提供了RSM软件工具的介绍与操作指南，并探讨了RSM在产品研发中面临的挑战和未来应用前景。通过对RSM的系统性阐述，本文旨在为工程师和研发人员提供实用的方法论，以实现产品研发过程的高效优化。

# 关键字
响应曲面方法；统计实验设计；数学模型；产品优化；软件工具；多目标优化

参考资源链接：[Design-Expert响应曲面分析教程：Box-Behnken设计详解](https://wenku.csdn.net/doc/3ew3dgk40j?spm=1055.2635.3001.10343)
# 1. 响应曲面方法（RSM）简介

响应曲面方法（Response Surface Methodology, RSM）是一种用于建模和优化多变量过程的统计技术。它通过结合实验设计、数学建模和优化技术，旨在发现影响输出（响应变量）的显著因素，并找出最优的工艺参数设置。

## 2.1 RSM的核心价值

RSM的引入显著提高了产品和过程设计的效率。通过建立一个关于一个或多个响应变量的输入因子的数学模型，RSM可以帮助研究者理解这些因子是如何影响响应变量的，并找到最佳的操作条件。

## 2.2 实际应用的两个主要场景

- 在产品研发中，RSM用于确定最佳的配方和加工条件。
- 在质量控制中，RSM用于诊断和优化生产过程，以减少变异性。

接下来的章节将详细探讨RSM的理论基础、实际应用以及在产品研发中的挑战与前景。

# 2. 响应曲面方法的理论基础

响应曲面方法（RSM）是统计学中用于建模和分析多个输入变量与一个或多个响应变量之间关系的一套方法。RSM不仅可以帮助我们理解变量之间的相互作用，还能通过优化响应变量的值来达到产品或工艺的改进。本章我们将深入探讨RSM的理论基础，从统计实验设计原理、响应曲面法的数学模型，到响应曲面优化策略，为您构建一个全面理解RSM的知识架构。

## 2.1 统计实验设计原理

### 2.1.1 实验设计的基本概念

实验设计是统计方法论的核心，它涉及计划和组织实验的细节，以确保数据收集的效率和有效性。实验设计的基本原则包括：

- **随机化**：为确保实验结果不受未知因素的影响，实验条件需要随机分配。
- **重复**：多次重复实验可以降低偶然误差的影响，提高实验结果的可靠性。
- **对照**：设置对照组有助于区分实验变量的真实效应与偶然因素的影响。

实验设计的目的是在最小的实验成本下，最大化信息量并准确估计实验因子对响应变量的影响。

### 2.1.2 实验设计的类型及其应用场景

实验设计可以分为几类：

- **完全随机设计**：适用于简单实验，其中所有实验单位被随机分配到不同的处理条件中。
- **随机区组设计**：当实验中的变异来源可以分为两类时使用，如时间或空间变异，可以控制这些变异对实验结果的影响。
- **因子实验设计**：当需要研究多个因子（输入变量）及其相互作用时使用，包括两水平因子实验设计（如2^k因子设计）和混合水平因子实验设计。

每种设计类型都有其适用的情景和优势，选择合适的实验设计对于获取可靠结论至关重要。

## 2.2 响应曲面法的数学模型

### 2.2.1 模型的建立与假设

响应曲面法通常利用数学模型来表示响应变量与一个或多个因子之间的关系。基本步骤包括：

1. **模型的选择**：通常采用多项式模型，如二次模型，以足够准确地捕捉响应曲面上的非线性关系。
2. **实验设计的选择**：利用中心组合设计（CCD）或Box-Behnken设计等来估计模型参数。
3. **模型的估计**：通过最小二乘法等统计方法，利用实验数据来估计模型中的系数。

模型建立的假设通常包括：

- **线性关系**：模型中的变量之间存在着线性关系。
- **独立性**：实验中的观测值相互独立。
- **方差齐性**：模型误差的方差是常数。
- **正态性**：模型误差项服从正态分布。

### 2.2.2 响应变量与因子间的关系

在响应曲面模型中，响应变量（y）通常表示为因子（x）的函数。例如，对于一个具有两个因子x1和x2的系统，二次模型可表示为：

y = β0 + β1x1 + β2x2 + β11x1^2 + β22x2^2 + β12x1x2 + ε

其中，β0、β1、β2、β11、β22和β12是模型参数，ε是误差项。

### 2.2.3 参数估计和方差分析

参数估计主要通过最小化预测值和实际观测值之间的差异来实现，即最小化残差平方和。常用的参数估计方法包括普通最小二乘法（OLS）和加权最小二乘法（WLS）。参数估计完成后，可以通过方差分析（ANOVA）来评估模型是否显著，以及模型各个项的贡献度。