【尾递归的优势与挑战】：现代编程语言中尾递归地位的深度剖析

# 1. 尾递归概念解析

尾递归是一种特殊的递归形式，它允许函数在返回调用自身的值时，无需额外的栈帧分配。这种优化方式对于提高程序的性能至关重要，尤其是在递归深度较大时。

## 1.1 递归的基本原理

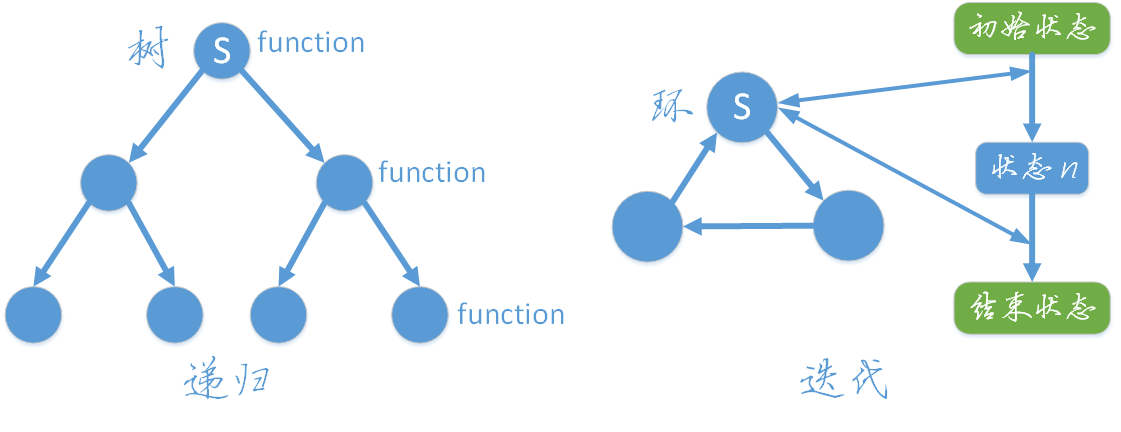
递归是一种常见的编程技术，它通过函数自己调用自己来解决问题。递归函数通常具有两个主要部分：基本情况和递归步骤。基本情况定义了递归结束的条件，而递归步骤则描述了如何通过缩小问题规模来逼近基本情况。

## 1.2 尾递归与非尾递归的区别

尾递归与非尾递归的主要区别在于函数执行的最后一个操作是否为递归调用。在尾递归中，递归调用是函数的最后一个动作，这使得编译器可以进行优化，重用当前的栈帧，而不是创建新的栈帧。这样的优化避免了栈溢出的风险，并减少了内存的使用，因为它不需要保存上一层递归的状态。

# 2. 尾递归的理论基础

## 2.1 递归的基本原理

### 2.1.1 递归的定义与函数自调用

递归是一种在程序设计语言中广泛应用的编程技术，它允许一个函数直接或间接地调用自身。这种自我调用的特性使得某些问题可以用非常简洁的方式来解决，特别是那些可以分解为相似子问题的问题。递归函数通常包含两个主要部分：基本情况（base case），它是递归结束的条件；以及递归步骤（recursive step），它将问题分解为更小的子问题，并递归地调用自身来解决这些子问题。

def factorial(n):
    if n == 0:  # 基本情况
        return 1
    else:
        return n * factorial(n-1)  # 递归步骤

在上述Python代码中，`factorial` 函数是一个递归函数，它通过递归调用自身来计算阶乘。当`n`等于0时，函数返回1作为基本情况的结果，否则函数将调用自身计算`n-1`的阶乘，并将其结果乘以`n`。

### 2.1.2 递归算法的时间复杂度分析

递归算法的时间复杂度分析是理解和优化递归函数的关键。通常，递归函数的时间复杂度与其递归深度成指数关系。这是因为每次递归调用都会产生新的函数调用实例，增加了调用栈的深度。对于一些递归算法来说，如果不进行优化，其时间复杂度可能非常高，甚至达到指数级。

graph TD
    A[开始] --> B{n == 0?}
    B -- 是 --> C[返回1]
    B -- 否 --> D[n * factorial(n-1)]
    D --> E[返回D的结果]
    E --> F[结束]

以阶乘函数为例，当输入为`n`时，其递归深度为`n`，因此其时间复杂度为O(n)。这意味着随着输入值的增加，运行时间将呈线性增长。然而，并非所有递归算法都能以这种方式简单分析，特别是那些非线性递归，或者涉及多个递归调用的算法。

## 2.2 尾递归与非尾递归的区别

### 2.2.1 尾调用优化的原理

尾调用优化（Tail Call Optimization，TCO）是一种特殊的编译器优化技术。当一个函数的最后一个动作是调用另一个函数（即尾调用）时，编译器可以重用当前函数的栈帧，而不是为尾调用创建一个新的栈帧。这种优化可以显著减少内存消耗，并且在理论上可以将递归算法的时间复杂度降低到O(1)。

尾调用优化的原理主要基于以下几点：

1. 当前函数执行完毕后，除了返回值之外的所有数据都已经不再需要。
2. 尾调用的函数可以使用相同的调用栈空间来执行，因为不需要返回到当前函数的调用者。
3. 通过这种方式，编译器可以避免递归深度增加时的栈溢出问题。

### 2.2.2 尾递归的编译器优化机制

尾递归是尾调用的一种特殊情况，特指函数以递归形式调用自身作为尾调用。尾递归优化机制要求编译器能够识别尾递归，并对其进行优化处理。以下是尾递归优化的主要步骤：

1. 识别尾递归：编译器需要分析函数以确认函数的最后一个动作是否为尾递归。
2. 优化转换：编译器将尾递归转换为跳转语句，这样可以重复使用栈帧。
3. 参数更新：在跳转之前，编译器会更新尾递归所需的参数，这些参数通常是函数的局部变量。

def tail_factorial(n, accumulator=1):
    if n == 0:
        return accumulator
    else:
        return tail_factorial(n-1, accumulator * n)

在Python中，尾递归优化并不总是自动进行，部分原因是Python的解释器并不总是优化尾递归调用。在支持尾调用优化的语言中（例如Erlang或Scheme），尾递归可以更加高效。

## 2.3 尾递归的数学和逻辑基础

### 2.3.1 数学归纳法与尾递归的联系

数学归纳法是证明与自然数相关的命题的一种常用方法，它包含两个步骤：基础步骤和归纳步骤。基础步骤证明命题在起始自然数上成立；归纳步骤证明如果命题在某个自然数上成立，那么它在下一个自然数上也成立。这种结构与尾递归有着密切的联系，因为它本质上是一种递归过程。

尾递归在实现数学归纳法证明时非常有用，因为它可以自然地模拟从一个数到下一个数的过程，而不是使用传统递归那样在每个步骤都创建新的栈帧。

### 2.3.2 逻辑编程中的尾递归应用

逻辑编程语言如Prolog使用尾递归来实现事实和规则的匹配。在逻辑编程中，递归经常用于描述集合内的元素，尾递归在这里能够有效地处理无限数据结构，如列表或树。尾递归逻辑编程模型可以提供更清晰和简洁的方式来表达逻辑关系。

factorial(0, 1).
factorial(N, F) :- N > 0, Prev is N-1, factorial(Prev, PrevF), F is N * PrevF.

在上述Prolog代码中，`factorial`关系定义了计算阶乘的逻辑。Prolog的查询引擎会从基本情况开始，使用尾递归的方式逐步解决递归调用。

下一章节，我们将深入探讨尾递归在现代编程语言中的实现，包括支持尾递归的语言概览、编译器优化实例分析以及尾递归优化的局限性与挑战。

# 3. 尾递归在现代编程语言中的实现

## 3.1 尾递归支持的语言概览

### 3.1.1 函数式编程语言中的尾递归

函数式编程语言如Haskell、Erlang、Scala等是尾递归优化的天然支持者。这些语言的设计哲学倾向于提供更为纯粹的函数式特性，包括对尾递归的支持。例如，在Haskell中，所有递归调用都被视为可能的尾调用，编译器会自动进行尾调用优化。

-- Haskell 中的斐波那契数列的尾递归实现
fibTailRec :: Integer -> Integer -> Integer -> Integer
fibTailRec a b 0 = a
fibTailRec a b n = fibTailRec b (a+b) (n-1)

-- 使用尾递归计算斐波那契数列
fib n = fibTailRec 0 1 n

在上述Haskell代码中，`fibTailRec` 函数通过尾递归的方式计算斐波那契数列，`fib` 函数是一个简化的接口。

### 3.1.2 命令式编程语言中的尾递归支持

命令式编程语言通常不直接提供尾递归优化，但在一些现代版本中已经开始加入了这种支持。比如，在Java 8及以上版本中，可以使用`@tailrec` 注解来标识尾递归函数，编译器会尝试将其优化为循环结构。

import java.lang.annotation.*;

@Retention(RetentionPolicy.SO