尾递归在算法竞赛中的运用：解题技巧与案例深度分析

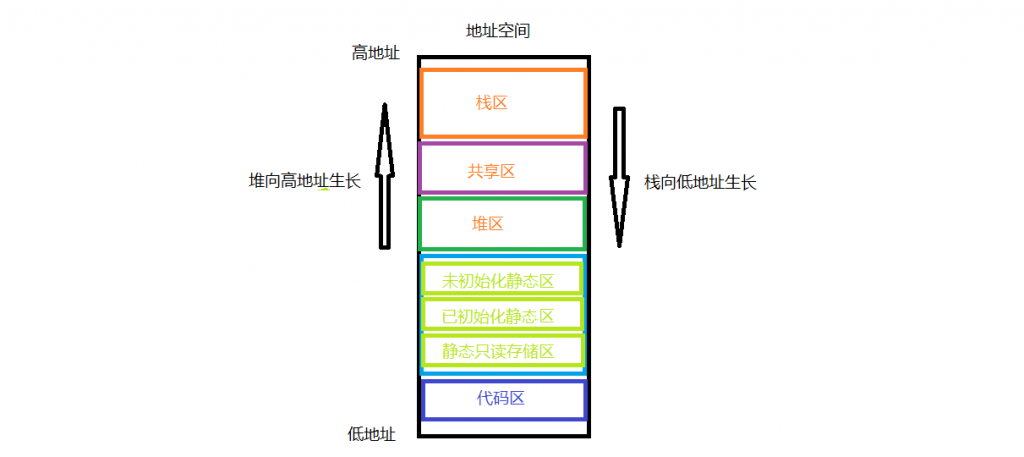
# 1. 尾递归基础理论与算法概念

递归是编程中一种强大的工具，它允许函数调用自身来解决问题。尾递归是递归的一种特殊形式，它将递归调用作为函数的最后一个操作。这种特性使得尾递归特别适合于优化，因为它可以减少函数调用栈的深度，避免栈溢出的风险。

## 1.1 递归的概念

递归函数包含两个基本部分：基本情况和递归情况。基本情况是递归的终止条件，而递归情况则是在每次函数调用中逐渐接近这个基本情况的过程。简单的例子如计算阶乘函数 `factorial(n) = n * factorial(n-1)`。

## 1.2 尾递归与普通递归的比较

普通递归在每次递归调用之后还需要执行返回前的操作，比如乘法操作。这导致了调用栈的增长，可能造成栈溢出。尾递归则不同，因为递归调用是函数体中的最后一个操作，编译器可以优化这一过程，通过重用当前的栈帧来避免增加新的栈帧。这样，尾递归在理论上能够像迭代一样高效，且保持递归的简洁性。

# 2. 尾递归优化原理与技术

## 2.1 尾递归的定义与特性

### 2.1.1 递归的概念

递归是一种常见的编程技巧，它允许一个函数直接或间接地调用自身来解决问题。递归函数通常包含两个基本部分：基本情况（base case）和递归情况（recursive case）。基本情况是递归结束的条件，通常对应于问题的最简形式。递归情况则会缩小问题规模，向基本情况靠近。递归的核心在于自引用，函数通过调用自身逐步深入问题的核心，直到达到基本情况。

递归在解决一些问题时非常直观和有力，如遍历树形结构、分治算法、组合数学问题等。然而，递归调用自身也带来了额外的开销，特别是随着递归深度的增加，它会消耗大量的栈空间，容易导致栈溢出错误。这也是为什么尾递归成为了一个值得研究的话题。

### 2.1.2 尾递归与普通递归的比较

尾递归是递归的一个特殊形式，它指的是在函数的尾部进行递归调用，并且不进行任何额外操作（例如加法、赋值等）。在尾递归中，函数的最后一次操作是调用自身，这样可以保证在递归过程中，当前函数的状态不再需要保存，新的函数调用可以直接复用当前栈帧。这便是尾递归与普通递归的主要区别。

在普通递归中，每一次递归调用都会创建一个新的栈帧来保存当前的状态信息，这意味着随着递归深度的增加，所需的栈空间会成倍增加。而在尾递归中，编译器或解释器可以优化这一过程，通过重用函数的栈帧来减少空间的使用，从而允许算法在理论上进行更深的递归而不会导致栈溢出。

## 2.2 尾递归的优化机制

### 2.2.1 编译器如何优化尾递归

现代的编译器为了提升程序的效率和运行时性能，通常会对尾递归进行特别的优化。编译器优化尾递归的基本思想是避免创建新的栈帧，而是重用当前的栈帧来执行下一次函数调用。在编译的过程中，尾递归被转换为一个跳转指令，指向函数的开始位置，但在此之前，它会更新所有必要的参数和局部变量。

具体来说，在某些编译器优化级别下，编译器会识别出尾递归调用，并将当前函数的状态（包括参数、局部变量等）保存在一个固定的位置。然后，它执行一个跳转指令回到函数的入口点，并带上新的参数值。这样，每次递归调用时，实际上并没有创建新的栈帧，而是在现有的栈帧上更新状态，继续执行。

### 2.2.2 减少栈空间使用的原理

栈空间的减少是尾递归优化的核心目的。在没有优化的情况下，每一次函数调用都需要分配一定的栈空间来保存函数的状态，包括局部变量和返回地址。随着递归深度的增加，这些栈空间的累加很快就会消耗大量内存资源，这在处理大规模数据或进行复杂计算时尤为明显。

通过尾递归优化，编译器将尾递归调用转换为一个类似循环的结构，仅使用一次栈帧，不断地更新状态并跳转回函数的起始位置。这种方法将原本的递归树结构转换为迭代结构，从而大大减少了栈空间的需求。因为编译器知道在尾递归调用之后不需要保存任何其他状态，所以可以放心地重用当前栈帧，而不是每次都开辟新的栈帧。

## 2.3 实现尾递归的算法策略

### 2.3.1 迭代转尾递归的方法

在实际编程中，许多递归算法都可以被转换成迭代形式。但是，在某些情况下，递归的表述更为直观和简洁。因此，了解如何将迭代算法转换为尾递归形式是很有帮助的。这通常涉及到添加一个或多个辅助参数来保存迭代过程中的中间状态，将非尾递归的递归调用转换为尾递归调用。

具体来说，你可以通过引入一个额外的参数来跟踪算法的状态，比如在一个斐波那契数列的计算中，我们可以使用一个额外的参数来跟踪当前计算到哪一阶。每次递归调用时，我们更新这个参数，直到达到基本情况。这种转换的关键在于确保递归调用是函数体中的最后一条语句，并且不包含其他表达式或操作。

下面是一个简单的例子来展示如何将迭代算法转换为尾递归形式：

-- 非尾递归的斐波那契数列计算（迭代形式）
fib n = let helper a b 0 = a
            helper a b count = helper b (a+b) (count-1)
        in helper 0 1 n

-- 尾递归形式的斐波那契数列计算
fib' n acc1 acc2 = if n == 0 then acc1 else fib' (n-1) acc2 (acc1+acc2)

在这个例子中，`fib`函数使用了一个辅助函数`helper`来追踪当前的斐波那契数和下一个斐波那契数。通过使用尾递归形式的`fib'`，我们将这个辅助函数的参数直接暴露给用户，使其可以简单地调用`fib'`函数而不必担心内部的迭代过程。

### 2.3.2 尾递归算法设计要点

在设计尾递归算法时，需要考虑几个关键点以确保其正确性和效率：

- **保证尾递归调用是函数的最后一个操作**：这保证了编译器可以进行尾调用优化，避免额外的栈空间使用。
- **合理设计递归参数**：通常需要引入额外的参数来保存之前的状态信息，确保递归调用可以正确地继续执行。
- **注意参数的更新方式**：在每次递归调用时，需要正确地更新状态参数，以保证算法的正确逻辑。
- **识别基本情况**：基本情况是递归结束的标志，正确设置基本情况对算法的正确执行至关重要。

此外，为了编写出高效的尾递归算法，还需要对目标编程语言的编译器优化机制有所了解。不同的编程语言和编译器对尾递归优化的支持程度不同，了解这些差异可以帮助我们在特定环境中写出更优的代码。在支持尾递归优化的语言中，编写尾递归算法时要注意保持函数的尾调用形式，并避免使用额外的表达式或操作来干扰尾调用的优化。

在下一章节，我们将深入探讨尾递归在算法竞赛中的应用，以及它如何帮助解决经典问题，并提高算法的效率和性能。

# 3. 尾递归在算法竞赛中的应用

在现代算法竞赛中，尾递归作为一种优化递归算法的策略，因其能够在编译阶段进行栈空间的优化而变得十分重要。本章我们将深入探讨尾递归在解决经典问题、结合动态规划以及在实际案例中的应用。

## 3.1 尾递归解决经典问题

尾递归在算法竞赛中解决经典问题时，往往能大幅度减少内存的使用，这对于需要在有限资源下解决问题的竞赛环境尤为重要。

### 3.1.1 经典递归问题与尾递归解法

许多经典的递归问题，如汉诺塔、斐波那契数列、图的遍历等，都可以通过尾递归的方式重新设计算法来解决。这种解法具有优化后的空间复杂度优势。例如，传统的斐波那契数列计算方法是：

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

这样的递归计算会导致大量的重复计算，而通过尾递归方法，可以将空间复杂度降至O(1)：

def fibonacci_tail(n, a=0, b=1):
    if n == 0:
        return a
    return fibonacci_tail(n-1, b, a+