【递归与动态规划比较】：Hackerrank递归问题解题秘诀

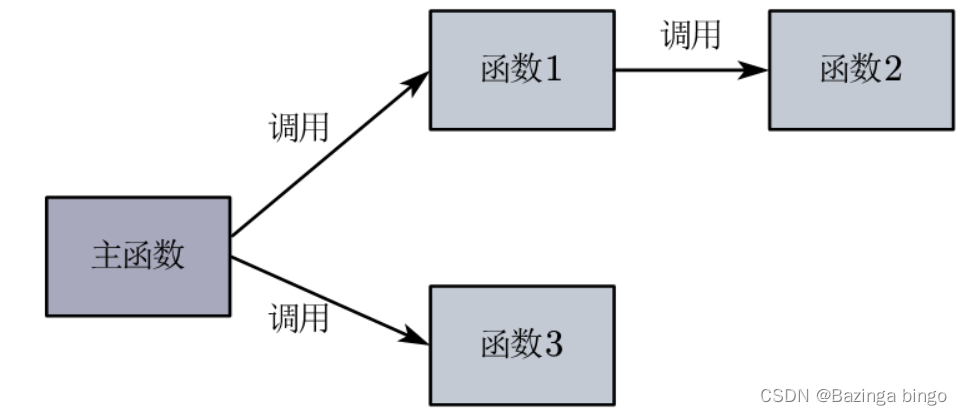
# 1. 递归与动态规划的概念解析

递归和动态规划是计算机科学中的两个基本概念，它们在解决复杂问题时发挥着重要作用。递归是一种算法设计方法，它允许函数调用自身来解决问题。递归的核心是将一个大问题分解成更小的相似问题，直至达到可以直接解决的简单问题。动态规划则是一种解决多阶段决策问题的方法，它通常用来优化递归算法以避免重复计算，提高效率。

本章我们将探讨这两个概念，并进行详细解析，为后续章节中深入探讨理论和实践打下坚实基础。首先，我们从递归的基本原理和特点入手，随后转向动态规划的理论框架，初步了解其背后的数学原理。这将为我们后续章节中讨论具体算法实践和应用场景奠定基础。

# 2. 递归算法的理论与实践

## 2.1 递归的基本原理
### 2.1.1 递归的定义和特性
递归是一种常见的编程技术，它允许函数调用自身来解决问题。递归的关键在于将问题分解成更小、更易于管理的部分，最终达到一个简单的、可以直接解决的基准情况。递归方法通常包含两个主要部分：基本情况（base case）和递归情况（recursive case）。

**基本情况**通常是问题的最小实例，可以通过直接的方法解决，不需要进一步的递归调用。

**递归情况**则将问题缩小至更小的规模，然后通过递归调用自身来解决。

递归的特性包括：
- **自引用**：函数直接或间接地调用自身。
- **重复性**：递归函数重复执行相似的子任务。
- **终止条件**：必须有终止递归的条件，以防止无限递归。

### 2.1.2 递归的工作原理
递归的工作原理基于“栈”的概念，它是一种数据结构，按照后进先出（LIFO）的原则存储信息。在递归调用中，每次函数调用都会在栈中添加一个新的帧（frame），其中包含该次调用的信息。当函数返回时，当前帧会从栈中弹出，并返回到之前的状态。

递归函数的调用顺序可以用以下步骤概括：
1. 检查是否满足基本情况。
2. 如果不满足，将问题分解成更小的子问题并递归调用自身。
3. 每次递归调用都会进入一个新的函数帧。
4. 当达到基本情况时，开始返回结果。
5. 每个返回的函数帧都会继续执行剩余的部分，并返回到上一个函数帧。
6. 最终返回最初的函数调用结果。

## 2.2 递归算法的经典案例分析
### 2.2.1 斐波那契数列的递归实现
斐波那契数列是一个经典的递归问题，它由以下递归关系定义：
- F(0) = 0
- F(1) = 1
- F(n) = F(n-1) + F(n-2) 对于 n > 1

下面是一个简单的递归实现：

def fibonacci(n):
    # 基本情况
    if n <= 1:
        return n
    # 递归情况
    else:
        return fibonacci(n-1) + fibonacci(n-2)

然而，这种简单的递归实现非常低效，因为它会重复计算许多子问题。这可以通过“记忆化搜索”（Memoization）来优化。

### 2.2.2 汉诺塔问题的递归解法
汉诺塔问题是一个经典的递归问题，它要求将一组不同大小的盘子从一个柱子移动到另一个柱子，遵循以下规则：
1. 每次只能移动一个盘子。
2. 任何时候，在三个柱子中的任何一个上，较大的盘子不能在较小的盘子上面。

这个问题的递归解决方案如下：

def hanoi(n, source, target, auxiliary):
    if n > 0:
        # 将n-1个盘子从源移动到辅助柱子
        hanoi(n-1, source, auxiliary, target)
        # 将最大的盘子从源移动到目标柱子
        print(f"Move disk {n} from {source} to {target}")
        # 将n-1个盘子从辅助柱子移动到目标柱子
        hanoi(n-1, auxiliary, target, source)

## 2.3 递归算法的优化技巧
### 2.3.1 记忆化搜索
记忆化搜索是一种优化递归算法的技术，它避免了重复计算相同的子问题。这通常是通过将子问题的解存储在缓存中实现的，如果再次遇到相同的子问题，则直接返回缓存的值，而不是重新计算。

### 2.3.2 尾递归优化
尾递归是函数递归调用时，如果它是函数体内的最后一个操作，则称为尾递归。一些编程语言和编译器支持尾递归优化，可以将尾递归转换为迭代，避免栈溢出并节省内存。

以下是使用尾递归解决斐波那契数列的示例：

def fibonacci_tail(n, a=0, b=1):
    if n == 0:
        return a
    else:
        return fibonacci_tail(n-1, b, a+b)

通过使用尾递归，我们确保了每次递归调用都是函数的最后一个操作，这有助于编译器或解释器进行优化。

# 3. 动态规划算法的理论与实践

在探讨动态规划之前，我们需要对这个算法有一个清晰的认识。动态规划是一种通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。它在许多领域，特别是在计算机科学和运筹学中得到了广泛的应用。动态规划不仅被用于求解数学问题，还广泛应用于生产调度、资源分配、决策制定等领域。本章我们将深入探讨动态规划的理论框架，并通过具体问题案例来实现动态规划算法。

## 3.1 动态规划的理论框架

### 3.1.1 动态规划的基本思想

动态规划的基本思想是把原始问题分解为相对简单的子问题，通过求解子问题来构造原始问题的解。这一过程不是简单地求解一次子问题，而是将子问题的解存储下来，以避免重复计算，提高效率。这种策略被称为“记忆化”。

动态规划解决问题的关键在于状态的定义与转移。状态通常是指解决问题过程中的某一阶段或时刻，而状态转移则是指如何从前一个或几个状态达到当前状态的过程。动态规划的复杂性在于选择合适的状态表示以及找到正确的状态转移方程。

### 3.1.2 动态规划的数学原理

动态规划的数学基础涉及递推关系和最优子结构两个核心概念。递推关系是指问题的最优解包含其子问题的最优解，而最优子结构则是指问题的最优解包含其子问题的最优解。

动态规划算法通常采用“自底向上”的方法，从最小的子问题开始，逐步扩展到大问题的解。这个过程中，需要用到迭代的计算方式来填满一张表，这张表通常称为动态规划表或者DP表。

## 3.2 动态规划算法的实现步骤

### 3.2.1 状态定义与状态转移方程

状态定义是动态规划中的第一步，它定义了子问题的解决方案。状态必须能够代表问题求解过程中的关键信息，而且要尽量保证状态的独立性，即后序状态的计算不应该依赖于已经计算过的状态。

状态转移方程描述了从一个或多个较小状态转移到当前状态的规则。找到合适的状态转移方程是解决问题的关键，也是动态规划中最具有挑战性的部分之一。

### 3.2.2 初始化与边界条件

在动态规划算法的实现中，需要特别注意初始化与边界条件的处理。初始化是指在DP表中填入初始值，这些初始值通常是问题的最小子问题的解。边界条件则是指DP表中的边界元素，它们的值通常是已知的