【图论与搜索策略】：Hackerrank DFS和BFS问题精通指南

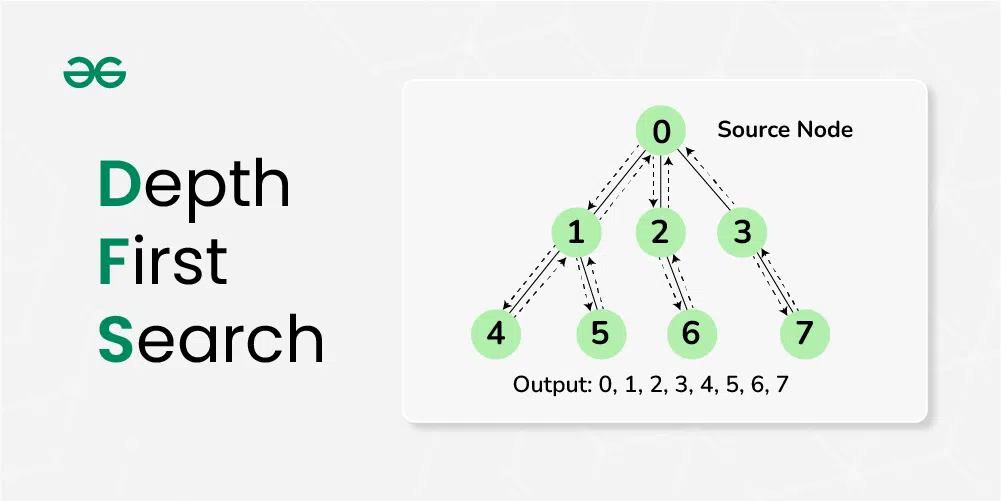
# 1. 图论基础与搜索算法概述

## 1.1 图论的基本概念
图论是数学的一个分支，主要研究的是图的性质，以及与图相关的算法。图由节点（顶点）和连接这些节点的边组成。有向图中的边有方向，而无向图中的边则没有。图可以用来表示各种实际问题中的关系和网络，例如社交网络、互联网、电路和交通网络等。

## 1.2 图的分类
根据图的特性可以将其分为多种类型：
- 简单图：没有重边和自环的图
- 加权图：边具有权重，表示连接顶点之间的成本或距离
- 完全图：图中任意两个不同顶点之间都存在一条边
- 二分图：图的顶点可以划分为两个互不相交的集合，任何一条边的两个端点都分别属于这两个集合

## 1.3 搜索算法的类型与作用
搜索算法用于在图中找到从起始点到目标点的路径。常见的搜索算法包括深度优先搜索（DFS）和广度优先搜索（BFS）。DFS通过递归深入每一条可能的分支，而BFS则逐层展开搜索，直到找到目标。

- **深度优先搜索（DFS）**：适用于路径查找和拓扑排序等应用。它通过递归的方式，优先探索图的深度。
- **广度优先搜索（BFS）**：常用于最短路径问题。它使用队列结构，从起始点开始，逐层访问所有邻接点。

这两种搜索算法在解决实际问题时，如导航、网络爬虫、游戏设计等领域中扮演了重要角色。在后续章节中，我们将深入探讨它们的原理、优化和应用场景。

# 2. 深度优先搜索（DFS）详解

### 2.1 DFS理论基础

深度优先搜索（DFS）是一种用于遍历或搜索树或图的算法。在图的遍历中，DFS会尽可能深地搜索图的分支，当节点v的所有边都已被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。深度优先搜索利用栈数据结构来实现。

#### 2.1.1 图的遍历与搜索算法概述

在图论中，图可以分为有向图和无向图两种。对于图的遍历，主要有两种基本算法：深度优先搜索（DFS）和广度优先搜索（BFS）。这两种算法有着不同的应用场景和特点。DFS在需要搜索尽可能深的路径时非常有效，而BFS则更适合寻找最短路径。

在DFS中，探索尽可能远的分支，并且在回溯之前不探索邻近分支，可以看作是一种“深挖”策略。而BFS则从源点开始，逐层向外扩展，像是“广撒网”。在实现DFS时，可以使用递归或显式栈数据结构来追踪路径。

#### 2.1.2 DFS的原理与递归实现

DFS可以使用递归或非递归（迭代）的方式实现。递归实现更直观，但可能会受到递归深度限制。以下是DFS的递归实现伪代码：

DFS(node):
  if node is visited:
    return
  mark node as visited
  perform action on node
  for each neighbor of node:
    DFS(neighbor)

在实际代码实现中，通常需要一个额外的数据结构（如数组或字典）来标记每个节点是否已经被访问过，以避免无限循环和重复访问。

### 2.2 DFS在Hackerrank中的应用

#### 2.2.1 常见DFS问题解析

在Hackerrank等编程竞赛平台上，DFS常常用于解决需要遍历或搜索的问题。例如，在解决迷宫问题时，我们需要从起点开始，使用DFS寻找到达终点的路径。常见的DFS问题还包括图的连通性判断、求解图中环或路径等问题。

#### 2.2.2 DFS优化技巧和代码实践

DFS的优化主要集中在减少不必要的搜索和加快搜索速度上。一种常见的方式是使用剪枝技术，即在搜索过程中发现某些条件下可以提前结束该分支的搜索。

下面是一个简单的DFS代码示例，展示了如何在Python中实现DFS并进行剪枝优化：

def DFS(graph, node, visited):
    if node is the solution:
        process_solution()
        return
    visited.add(node)
    for neighbour in graph[node]:
        if neighbour not in visited:
            DFS(graph, neighbour, visited)

# 初始化图和搜索节点
graph = build_graph()
start_node = get_start_node()
visited = set()
DFS(graph, start_node, visited)

### 2.3 DFS的高级应用

#### 2.3.1 DFS变种：双向搜索与迭代加深搜索

双向搜索是从源点和目标点同时进行深度优先搜索，直到两者相遇，这种方法在解决某些问题时可以有效减少搜索空间。迭代加深搜索是深度优先搜索的另一种变体，它通过限制搜索深度来避免陷入过深的路径，然后逐步增加深度限制，直到找到解。

#### 2.3.2 DFS与图着色、拓扑排序等经典问题

DFS与图着色问题结合时，可以用于检测图中是否存在环。如果在DFS的递归过程中，发现一个已访问过的节点，说明存在环。对于有向无环图（DAG），DFS可以用来进行拓扑排序，即将图中的所有节点线性排序，使得对于图中的每一条有向边(u, v)，节点u都在节点v之前。

在实际应用中，DFS不仅是一种强大的搜索工具，它还帮助开发者更好地理解图的结构和性质，从而在各种复杂的图论问题中找到解法。在下一章中，我们将探讨广度优先搜索（BFS），这是一种与DFS有着不同特性和应用场景的搜索策略。

# 3. 广度优先搜索（BFS）详解

## 3.1 BFS理论基础

### 3.1.1 BFS的基本原理与队列实现

广度优先搜索（BFS）是一种用于遍历或搜索树或图的算法。它的核心思想是从某一节点开始，先访问它的所有邻近节点，然后再对每个邻近节点逐层进行访问，直到所有的节点都被访问过。BFS使用队列数据结构来跟踪每一层待访问的节点，从而保证算法以广度优先的方式进行。

BFS的伪代码如下：

BFS(G, s) // G为图，s为起始节点
    let Q be a queue
    Q.enqueue(s)
    while Q is not empty
        v = Q.dequeue()
        if v is the goal
            return v
        for all edges from v to w in G
            if w is unmarked
                mark w
                Q.enqueue(w)

在队列实现中，我们通常使用两个标志位，一个用于标记节点是否已经被访问过，另一个用于标记节点是否在当前层。这有助于提高算法的效率，确保我们不会重复访问一个节点，并且可以在每一层遍历结束后正确地切换到下一层。

### 3.1.2 BFS在树和图中的应用差异

BFS在树和图中应用有一些本质的区别。在树中，由于其结构特性（无环且每个节点只有一个父节点），BFS可以直观地一层层遍历所有节点。而在图中，由于可能存在环，BFS的实现需要额外的标记机制来避免重复访问。

在树的遍历中，BFS能够轻易地按层级访问节点，从而得到节点的层序遍历结果。但在图中，BFS则主要用于找到从源点到其他所有可达节点的最短路径，或者判断两个节点是否是连通的。

### 表格：BFS在树和图中应用对比

| 特性 | 树 | 图 |
| --- | --- | --- |
| 数据结构 | 层序遍历 | 最短路径搜索 |
| 路径特点 | 单一路径 | 多条路径可能性 |
| 访问顺序 | 按层访问 | 按访问顺序访问 |
| 避免重复访问 | 可通过访问标记实现 | 需要额外的标记机制（如使用HashSet记录访问过的节点） |

## 3.2 BFS在Hackerrank中的应用

### 3.2.1 常见BFS问题解