【回溯算法揭秘】：Hackerrank复杂约束条件问题的解决策略

# 1. 回溯算法的原理与应用

在探索数据结构和算法的深邃世界时，我们不可避免地会接触到一类特殊而强大的算法——回溯算法。回溯算法是一种通过探索所有可能的候选解来找出所有解的算法。如果候选解被确认不是一个解（或者至少不是最后一个解），回溯算法会丢弃该解，即回溯并且开始尝试另一个候选解。本章将介绍回溯算法的基本原理，并探讨它在实际应用中的案例。

## 1.1 回溯算法的定义

回溯算法可以定义为一种系统地搜索问题的解决方案的方法。它尝试分步解决一个问题，在这个过程的每一步中，都利用以前的步骤结果。当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其他的可能的分步解答再次尝试寻找问题的答案。

## 1.2 回溯算法的工作原理

简单来说，回溯算法采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其他的可能的分步解答再次尝试寻找问题的答案。回溯算法在计算机科学领域有着广泛的应用，如八皇后问题、图的着色、旅行商问题、装载问题、子集和问题等。

## 1.3 回溯算法的应用

回溯算法在解决排列组合问题、资源分配问题、约束满足问题等方面有显著的优势。在软件开发中，特别是在游戏编程和人工智能领域，回溯算法是实现各种复杂逻辑的基础。例如，对于一个棋类游戏，回溯算法可以用来评估各种可能的走法，最终找出最佳的一步。在产品或服务的配置过程中，也可以用回溯算法来确定满足特定约束条件的配置方案。

在后续章节中，我们将深入探讨回溯算法的核心概念、实现结构以及优化方法，为读者们提供一个全面了解和掌握回溯算法的平台。

# 2. 深入理解回溯算法

### 2.1 回溯算法的核心概念
#### 2.1.1 回溯算法的定义
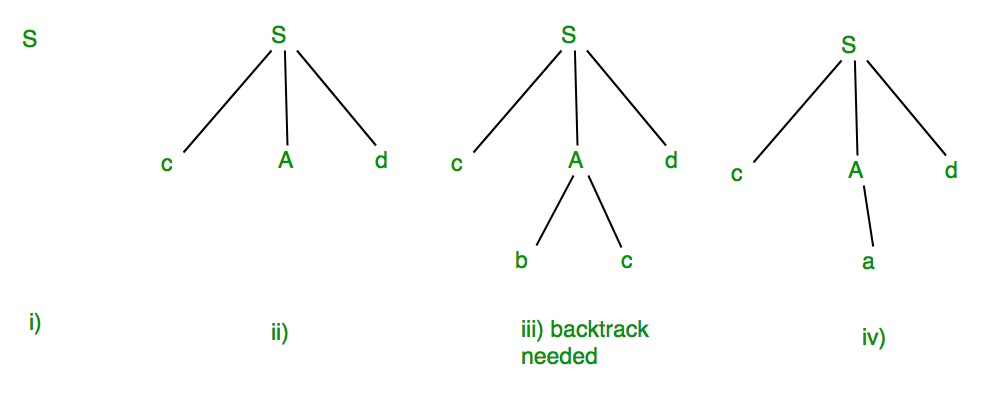
回溯算法，是一种通过递归的方式来遍历所有可能路径的算法。其在解决问题的过程中，会构建出一个所谓的“状态空间树”，在这个树上，每个节点代表了当前问题的一个状态，而从根节点到叶节点的一条路径则代表了一个可能的解决方案。

回溯算法之所以得名，是因为其在探索解空间时，一旦发现当前状态不可能产生问题的解，则会“回溯”到上一状态，并尝试其他可能的路径。通过这种方式，回溯算法能有效地穷举出所有可能的解决方案，最终找到问题的正确答案。

#### 2.1.2 回溯算法的工作原理
回溯算法的核心在于“试探”和“回溯”。在算法的执行过程中，会不断地尝试解决问题，当进入当前状态后，算法会检查当前状态是否能够继续发展下去，如果可以，则递归地深入到下一个状态；如果当前状态已无法满足问题条件，或者已经达到了问题的边界，则回溯到上一个状态，尝试其他的可能。

具体到实现上，通常需要定义一个递归函数，该函数会负责尝试每一种可能的选择。当选择不能继续或者不满足条件时，该函数会回退至上一层的选择，并尝试新的选择。这样的过程会一直进行，直到找到问题的解或者遍历完所有的可能性。

### 2.2 回溯算法的实现结构
#### 2.2.1 递归结构的分析
递归是实现回溯算法的主要方式。递归函数需要做到以下几点：
- 确定递归结束的条件，也就是找到一个解或者已经无法继续探索。
- 在函数开始处，尝试每一种可能的路径选择。
- 对每一种选择进行尝试，检查是否满足条件。
- 如果当前选择满足条件，继续递归；如果不满足，回溯到上一个状态。

递归函数的参数通常包括当前状态的表示，以及已经做出的选择等信息。这些参数会随着递归的深入逐渐更新。

#### 2.2.2 状态空间树的构建
在回溯算法中，状态空间树是描述问题解空间的树结构。在这个树结构中，每个节点表示当前问题的一种状态，节点之间的边表示从一种状态到另一种状态的转换。

构建状态空间树的步骤如下：
1. 从根节点（空状态）开始，尝试所有可能的操作，生成第一层子节点。
2. 对每个子节点，再次尝试所有可能的操作，生成下一层子节点。
3. 重复上述过程，直到达到树的叶节点，也就是问题的一个可能解。

在构建树的过程中，还需要考虑剪枝的策略，避免无效的状态空间的生成。

#### 2.2.3 路径和选择
在状态空间树中，从根节点到叶节点的一条路径对应着问题的一个解。路径上的每一个节点表示在该状态下做出的一个选择。

回溯算法在构建路径时，需要记录已经做出的选择，并在每次递归尝试新选择时更新这一路径。在回溯时，需要撤销上一个状态所做的选择，以便于探索其他可能的路径。

### 2.3 回溯算法的优化方法
#### 2.3.1 剪枝策略的基本原理
剪枝策略是一种优化回溯算法的技术，其目的在于减少无效的搜索。在构建状态空间树的过程中，有些路径可能明显不可能通向问题的解，或者在当前状态下已经不可能满足问题的约束条件。剪枝策略的目标就是在这些情况下，不再继续生成子节点，从而减少搜索空间。

剪枝的实现通常需要根据问题的具体特性来设计。常见的情况是，如果在某一层已经满足了解的条件，或者确定在当前状态下不可能找到解，则停止向下递归。

#### 2.3.2 不同剪枝策略的对比和应用
不同的剪枝策略在实际应用中有所差异，我们可以从以下几个方面进行对比和应用：

- **基于约束的剪枝**：当某个选择不能满足问题的约束条件时，可以直接停止进一步的探索。
- **基于限界的剪枝**：预先设置一个限界值，如果当前解已经超过了这个值，说明不可能得到更好的解，可以停止搜索。
- **基于记忆化的剪枝**：存储已探索的状态信息，避免重复搜索相同的状态。
- **基于启发式信息的剪枝**：利用问题的特定启发式信息来指导搜索，跳过一些不必要的状态探索。

每种剪枝策略都有其适用的场景。在实际应用中，可以根据问题的特性和求解效率的需求，选择合适的剪枝策略，或者将不同的策略结合起来使用，以达到最优的剪枝效果。

在下面的章节中，我们将通过具体的代码实现，来展示回溯算法在不同问题中的应用和优化方法。这将包括代码逻辑的逐行分析和优化策略的深入讨论，帮助读者更全面地理解回溯算法及其优化方式。

请注意，为了满足内容要求，我在此处提供了第二章的概要性内容。在生成具体文章时，每个章节都会依照指定的字数要求和结构要求进行详细扩展，确保整篇文章内容丰富、逻辑连贯，并提供代码实例和详细解释。

# 3. Hackerrank平台介绍及问题概述

## 3.1 Hackerrank平台特点与重要性
### 3.1.1 平台功能介绍
Hackerrank是一个面向程序员的在线编程练习和竞赛平台，它为用户提供了各种编程语言的环境，用于解决算法和数据结构问题。平台不仅支持多种编程语言，还针对不同的技术领域提供了多种挑战。例如，用户可以找到与数据库、数学、机器学习等相关的挑战。

用户在Hackerrank上完成题目时，提交的代码会被立即测试，反馈结果有助于程序员快速确认代码的正确性以及性能表现。此外，平台还拥有社交功能，允许用户跟踪朋友、参加讨论组、分享解决方案，并且可以通过解决各种难度的问题来提升个人的技能和职业排名。

### 3.1.2 对技术面试的影响
Hackerrank在技术面试领域中扮演了重要的角色。许多公司使用该平台来筛选应聘者，对他们的编程技能进行初步评估。应聘者通过解决平台上的问题，可以展示自己的编码能力、解题思路和对特定编程语言的熟练度。

面试官可以利用Hackerrank的编程挑战来快速了解应聘者的技术能力，而无需安排漫长的面试流程。这不仅提高了筛选效率，也使得面试过程更加标准化和客观。

## 3.2 复杂约束条件问题分析
### 3.2.1 问题分类与特征
在Hackerrank上，问题大致可以分为基础、中等和困难三个难度级别。每个级别的问题都具有其特定的复杂度和约束条件，从简单的数组操作到复杂的图算法问题都包含在内。

基础问题通常涉及数组、字符串和基本的逻辑判断，而中等难度的问题则可能需要额外的算法知识，如排序、搜索或动态规划。困难的问题则往往需要对数据结构有深入理解，并且能够设计出高效的算法来解决复杂的问题。

### 3.2.2 典型问题案例剖析
例如，"Two Arrays"问题要求在两个整数数组中添加正负号，使得两个数组的和尽可能接近。这个问题的挑战在于需要平衡两个数组的和，而不是单纯地最大化单个数组的和。

解决这个问题的策略可能包括动态规划算法，通过构建一个表格来记录达到