脚本自动化新高度：Python math库在问题解决中的应用

# 1. Python数学库概述

Python作为一种高级编程语言，拥有强大的数学库支持，广泛应用于科学计算、数据分析、机器学习等领域。本章我们将对Python的数学库进行一个全面的概述，从基础的数学计算到复杂的数学模型求解，让读者能够对Python在数学方面的应用有一个整体的认识。

首先，Python的数学库并不是单指一个库，而是多个库的集合，包括但不限于`math`, `cmath`, `numpy`, `scipy`等。这些库中包含了大量的函数和类，可以执行从基本的算术运算到复杂的数值分析和优化算法等各种数学操作。例如，`math`库提供了基本的数学函数如`sin`, `cos`, `log`等，而`numpy`库则是用于科学计算的核心库，提供了多维数组对象和众多数学函数操作。

Python的数学库因其简便易用和功能强大的特点，在处理数学问题时能够提供非常高效的解决方案。在接下来的章节中，我们将深入探索Python数学库的具体应用和高级技巧，帮助读者更好地利用这些工具来解决实际问题。

# 2. Python数学库基础

### 2.1 数学库中的基本数学运算

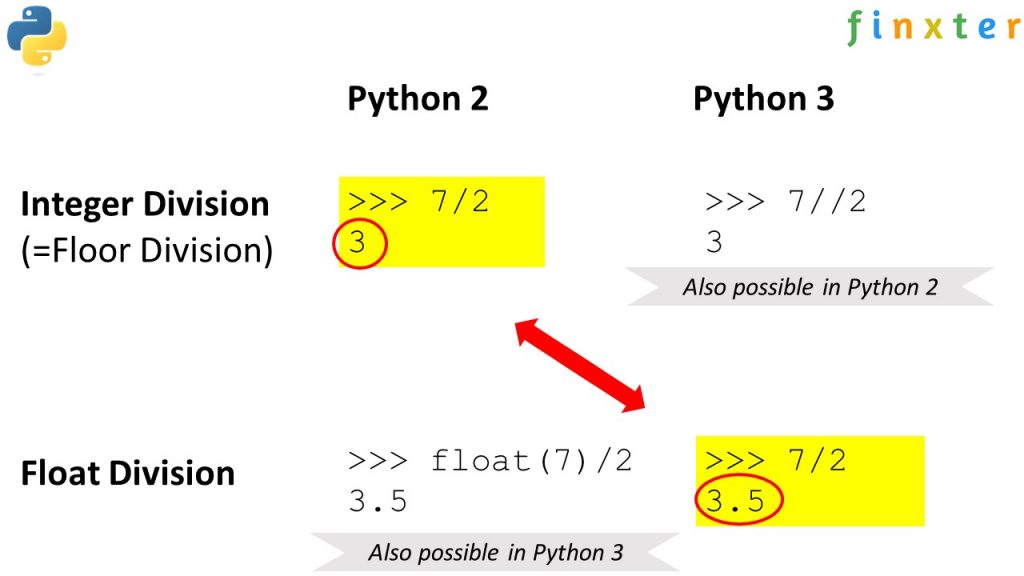
#### 2.1.1 算术运算

在Python中，使用数学库进行基本的算术运算（加、减、乘、除等）是通过内置的运算符直接实现的。当使用这些运算符对浮点数进行操作时，Python会自动处理舍入和精度问题。

import math

# 加法
sum_result = 2.5 + 3.2

# 减法
subtraction_result = 10.0 - 4.5

# 乘法
multiplication_result = 2.0 * 7.3

# 除法
division_result = 10.0 / 3.0

# 求余
remainder_result = 10 % 3

# 幂运算
power_result = 2.0 ** 3

print("Sum:", sum_result)
print("Subtraction:", subtraction_result)
print("Multiplication:", multiplication_result)
print("Division:", division_result)
print("Remainder:", remainder_result)
print("Power:", power_result)

以上代码展示了基本的算术运算和结果。Python数学库也提供了许多高级算术函数，比如求绝对值、最大值和最小值等。

# 绝对值
absolute_value = abs(-10.5)

# 最大值
max_value = max(10.5, 20.5, 30.5)

# 最小值
min_value = min(10.5, 20.5, 30.5)

print("Absolute value:", absolute_value)
print("Max value:", max_value)
print("Min value:", min_value)

在进行算术运算时，理解数据类型和操作符的优先级是非常重要的。例如，幂运算符`**`的优先级高于乘法`*`和除法`/`。

#### 2.1.2 三角函数和双曲函数

Python数学库提供了丰富的三角函数和双曲函数，这些函数对于执行各种数学和工程计算非常有用。

# 正弦函数
sin_value = math.sin(math.pi / 2)

# 余弦函数
cos_value = math.cos(0)

# 正切函数
tan_value = math.tan(math.pi / 4)

# 双曲正弦函数
sinh_value = math.sinh(1)

# 双曲余弦函数
cosh_value = math.cosh(1)

# 双曲正切函数
tanh_value = math.tanh(1)

print("Sin:", sin_value)
print("Cos:", cos_value)
print("Tan:", tan_value)
print("Sinh:", sinh_value)
print("Cosh:", cosh_value)
print("Tanh:", tanh_value)

三角函数通常接受弧度值作为输入，如果需要从角度转换到弧度，可以使用`math.radians()`函数。而`math.degrees()`函数则可以将弧度转换回角度。

以上介绍的内容仅是Python数学库中基础算术运算和三角函数的一小部分，但已经可以看出其在处理基本数学计算任务时的便利性和强大功能。这些函数是任何涉及到数学计算的Python应用不可或缺的部分。

# 3. Python数学库进阶技巧

在之前的章节中，我们介绍了Python数学库的基础使用，比如基本的算术运算、随机数生成和统计分析等。现在，让我们深入探讨一些更高级的技巧和应用，这些内容将为有经验的IT从业者提供更丰富的工具和方法，以解决更复杂的数学问题和科学计算。

## 3.1 复数和矩阵运算

### 3.1.1 复数的基本操作

在数学、物理和工程学的多个领域中，复数都是不可或缺的工具。Python的数学库同样提供了对复数操作的全面支持。复数在Python中表示为`a + bj`的形式，其中`a`是实部，`b`是虚部，`j`是虚数单位。

让我们来看一个如何使用Python进行复数运算的例子：

# 复数的基本操作
c1 = complex(3, 4) # 创建一个复数3+4j
c2 = complex(1, -2) # 创建另一个复数1-2j

# 复数的加法
c3 = c1 + c2
print(f"复数加法结果：{c3}") # 输出：(4+2j)

# 复数的减法
c4 = c1 - c2
print(f"复数减法结果：{c4}") # 输出：(2+6j)

# 复数的乘法
c5 = c1 * c2
print(f"复数乘法结果：{c5}") # 输出：(11+2j)

# 复数的除法
c6 = c1 / c2
print(f"复数除法结果：{c6}") # 输出：(0.44+2.44j)

### 3.1.2 矩阵运算和线性代数

矩阵运算在数据处理、图像处理、机器学习等领域中极为重要。Python通过多种库提供了矩阵运算的支持，其中最著名的是NumPy库。在处理矩阵时，我们常常用到的运算包括矩阵的乘法、求逆、特征值分解等。

让我们通过代码示例来理解如何进行矩阵