z域和s域之间的联系与转换方法

)

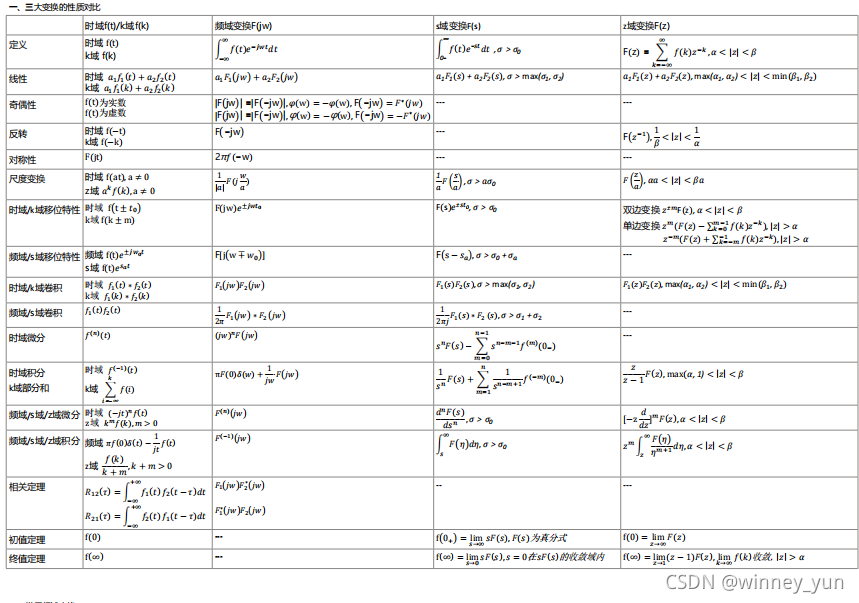# 1. 引言

## 1.1 背景

在现代科技和工程领域中，信号处理和控制系统是非常重要的研究方向。为了对信号和系统进行分析和设计，数学工具起着至关重要的作用。其中，z域和s域是两种常用的数学工具，用来描述信号和系统的特性和行为。

## 1.2 目的

本文旨在介绍和比较z域和s域的概念，并深入探讨它们之间的联系。我们将详细讨论z域和s域的数学关系以及它们在物理上的意义。此外，我们还将介绍从z域到s域的转换方法和从s域到z域的转换方法，并通过实际应用案例来说明它们的重要性。

接下来的章节将按照如下结构展开：首先介绍z域和s域的概述，然后讨论它们之间的联系，接着介绍转换方法，最后通过应用实例和案例分析来加深理解。最后，我们将总结z域和s域之间的联系，并展望未来的发展方向。让我们开始吧！

# 2. 什么是z域和s域

### 2.1 z域概述

z域是数字信号处理（DSP）中的一个核心概念，用于分析和设计离散时间系统。z域通过z变换将离散时间信号转换为复频域表示，使得我们能够更方便地处理信号的频率特性和系统的动态行为。

#### z变换的定义

z变换是将离散时间信号 \( x[n] \) 转换为z域信号 \( X(z) \) 的一种数学工具，其定义为：

\[
X(z) = \sum_{n=-\infty}^{+\infty} x[n] z^{-n}
\]

其中，\( z \) 是一个复数变量，通常表示为 \( z = re^{j\omega} \)，其中 \( r \) 是模，\( \omega \) 是相位角。

#### z域的特性

1. **频率响应**：通过将 \( z \) 替换为 \( e^{j\omega} \)，可以得到系统的频率响应。
2. **稳定性**：系统的稳定性可以通过分析其极点的位置来判断。如果所有极点都位于单位圆内，则系统是稳定的。
3. **离散时间卷积**：z域中的乘法对应于时域中的卷积，这使得系统的分析和设计更加简便。

#### 例子

考虑一个简单的离散时间系统，其输入信号为 \( x[n] = a^n u[n] \)，其中 \( u[n] \) 是单位阶跃函数。其z变换为：

\[
X(z) = \sum_{n=0}^{+\infty} a^n z^{-n} = \frac{1}{1 - az^{-1}}, \quad |z| > |a|
\]

这个表达式可以用来分析系统的频率响应和稳定性。

### 2.2 s域概述

s域是信号与系统理论中用于描述连续时间系统的频域特性的重要工具。通过拉普拉斯变换，时域信号可以被转换为s域信号，从而使得系统分析和设计变得更加直观和简便。

#### 拉普拉斯变换的定义

拉普拉斯变换是将连续时间信号 \( x(t) \) 转换为s域信号 \( X(s) \) 的一种数学工具，其定义为：

\[
X(s) = \int_{0}^{+\infty} x(t) e^{-st} dt
\]

其中，\( s \) 是一个复数变量，通常表示为 \( s = \sigma + j\omega \)，其中 \( \sigma \) 是实部，\( j\omega \) 是虚部。

#### s域的特性

1. **频率响应**：通过将 \( s \) 替换为 \( j\omega \)，可以得到系统的频率响应。
2. **稳定性**：系统的稳定性通过分析其极点的位置来判断。如果所有极点都位于左半平面内，则系统是稳定的。
3. **连续时间卷积**：s域中的乘法对应于时域中的卷积，这使得系统的分析和设计更加简便。

#### 例子

考虑一个简单的连续时间系统，其输入信号为 \( x(t) = e^{-at} u(t) \)，其中 \( u(t) \) 是单位阶跃函数。其拉普拉斯变换为：

\[
X(s) = \int_{0}^{+\infty} e^{-at} e^{-st} dt = \frac{1}{s + a}, \quad \text{Re}(s) > -a
\]

这个表达式可以用来分析系统的频率响应和稳定性。

### 2.3 z域与s域的联系

尽管z域和s域分别用于离散时间和连续时间信号处理，但它们之间存在一定的联系。可以通过双线性变换等方法将s域的系统转换为z域的系统，从而实现两者之间的相互转换。这种联系使得工程师能够在设计和分析系统时选择最合适的工具。

### 2.4 双线性变换

双线性变换是一种常用的方法，用于将连续时间系统（s域）转换为离散时间系统（z域）。这种方法通过将s域的复频率变量 ( s ) 映射到z域的复频率变量 ( z ) 来实现。双线性变换的主要优点是它能够保持系统的稳定性和频率响应特性。

#### 双线性变换的定义

双线性变换的公式如下：

[ s = \frac{2}{T} \cdot \frac{1 - z^{-1}}{1 + z^{-1}} ]

其中：

- ( s ) 是s域的复频率变量。
- ( z ) 是z域的复频率变量。
- ( T ) 是采样周期。

#### 步骤

1. **选择采样周期**：首先确定系统的采样周期 ( T )。

2. **应用双线性变换**：将s域中的传递函数 ( H(s) ) 通过双线性变换公式转换为z域的传递函数 ( H(z) )。

3. **替换s**：在s域的传递函数中，将 ( s ) 替换为双线性变换公式中的表达式：

[ H(z) = H\left(\frac{2}{T} \cdot \frac{1 - z^{-1}}{1 + z^{-1}}\right) ]

4. **化简**：对得到的表达式进行化简，得到z域的传递函数 ( H(z) )。

#### 例子

假设我们有一个简单的连续时间系统，其传递函数为：

[ H(s) = \frac{1}{s + 1} ]

我们希望将其转换为z域。假设采样周期 ( T = 1 )。

1. **应用双线性变换**：

[ s = \frac{2}{1} \cdot \frac{1 - z^{-1}}{1 + z^{-1}} = 2 \cdot \frac{1 - z^{-1}}{1 + z^{-1}} ]

2. **替换s**：

[ H(z) = H\left(2 \cdot \frac{1 - z^{-1}}{1 + z^{-1}}\right) = \frac{1}{2 \cdot \frac{1 - z^{-1}}{1 + z^{-1}} + 1} ]

3. **化简**：

[ H(z) = \frac{1 + z^{-1}}{2(1 - z^{-1}) + (1 + z^{-1})} = \frac{1 + z^{-1}}{2 - 2z^{-1} + 1 + z^{-1}} = \frac{1 + z^{-1}}{3 - z^{-1}} ]

4. **进一步化简**：

[ H(z) = \frac{z + 1}{3z - 1} ]

最终得到的 ( H(z) ) 就是该连续时间系统在z域中的表示。

#### 注意事项

- **频率映射**：双线性变换会导致频率的非线性映射，因此在设计数字滤波器时，需要注意频率响应的变化。
- **稳定性**：如果s域系统是稳定的，则通过双线性变换得到的z域系统也将是稳定的。
- **预畸变**：在某些情况下，为了更好地匹配频率响应，可能需要对s域的传递函数进行预畸变处理。

通过双线性变换，工程师可以有效地将连续时间系统转换为离散时间系统，从而在数字信号处理领域进行分析和设计。

# 3. z域和s域之间的联系

在信号与系统领域，z域和s域是两个重要的数学工具，它们在研究和分析连续时间和离散时间系统中起着关键的作用。本章将介绍z域和s域之间的联系，包括数学关系和物理意义。

#### 3.1 数学关系

z域和s域之间存在着一定的数学关系，可以通过一些转换方法将s域中的信号或系统转换到z域中进行分析。其中最常用的数学关系是z变换和拉普拉斯变换