高斯模型在自然语言处理中的作用：文本分类、主题建模的基石，构建自然语言处理的坚实基础

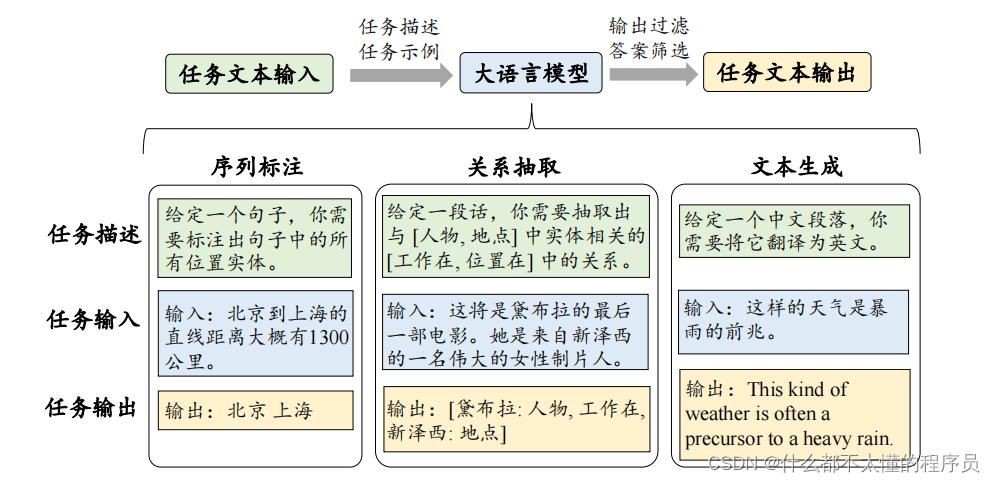
# 1. 高斯模型概述

高斯模型，也称为正态分布模型，是一种连续概率分布，其概率密度函数由以下公式表示：

f(x) = (1 / (σ√(2π))) * e^(-(x - μ)² / (2σ²))

其中，μ表示均值，σ表示标准差。高斯模型广泛应用于自然科学、工程和社会科学等领域，用来描述各种连续随机变量的分布情况。

在自然语言处理中，高斯模型主要用于文本分类和主题建模。文本分类是指将文本文档分配到预定义的类别中，而主题建模则是从文本数据中识别出潜在的主题或概念。高斯模型的概率分布特性使其能够有效地捕获文本数据的统计规律，从而实现文本分类和主题建模任务。

# 2. 高斯模型在文本分类中的应用

高斯模型在文本分类中发挥着至关重要的作用，提供了一种基于统计概率的分类方法。本章节将深入探讨高斯贝叶斯分类器和隐含狄利克雷分配（LDA）在文本分类中的应用。

### 2.1 高斯贝叶斯分类器

#### 2.1.1 原理和数学基础

高斯贝叶斯分类器是一种基于贝叶斯定理的分类器，其假设特征之间相互独立，且特征服从高斯分布。对于给定的文本样本，分类器计算每个类别的后验概率，并将其分配到具有最高后验概率的类别。

后验概率计算公式如下：

P(C | X) = (P(X | C) * P(C)) / P(X)

其中：

* P(C | X) 表示在观察到特征 X 时，样本属于类别 C 的后验概率
* P(X | C) 表示在类别 C 中观察到特征 X 的似然函数
* P(C) 表示类别 C 的先验概率
* P(X) 表示特征 X 的先验概率

#### 2.1.2 实际应用场景

高斯贝叶斯分类器广泛应用于各种文本分类任务，包括：

* 垃圾邮件过滤
* 情感分析
* 主题分类

### 2.2 隐含狄利克雷分配（LDA）

#### 2.2.1 模型原理和推导

隐含狄利克雷分配（LDA）是一种生成式模型，它假设文本是由一组潜在主题组成的。LDA 通过推断每个文档中主题的分布和每个主题中单词的分布来学习这些主题。

LDA 的数学基础如下：

P(w | d) = ∫ P(w | z) P(z | d) P(d) dz

其中：

* P(w | d) 表示在文档 d 中观察到单词 w 的概率
* P(w | z) 表示在主题 z 中观察到单词 w 的概率
* P(z | d) 表示在文档 d 中观察到主题 z 的概率
* P(d) 表示文档 d 的先验概率

#### 2.2.2 文本主题建模的应用

LDA 在文本主题建模中得到广泛应用，其主要应用场景包括：

* 文档聚类
* 文本摘要
* 关键词提取

# 3.1 潜在语义分析（LSA）

#### 3.1.1 模型原理和数学基础

潜在语义分析（LSA）是一种基于奇异值分解（SVD）的主题建模技术。其基本原理是将高维的文本数据降维到低维的语义空间，从而提取文本中的潜在语义信息。

LSA的数学基础如下：

给定一个文档-单词矩阵 $X$，其中 $X_{ij}$ 表示第 $i$ 个文档中第 $j$ 个单词的词频。对 $X$ 进行奇异值分解，得到：

$$X = U \Sigma V^T$$

其中 $U$ 和 $V$ 是正交矩阵，$\Sigma$ 是奇异值矩阵，对角线元素为 $X$ 的奇异值。

#### 3.1.2 文本相似度计算的应用

LSA提取的语义空间可以用于计算文本之间的相似度。通过将文本表示为低维语义向量，可以利用余弦相似度或欧氏距离等度量方法计算文本之间的相似度。

例如，给定两个文本向量 $v_1$ 和 $v_2$，其余弦相似度计算公式为：

$$sim(v_1, v_2) = \frac{v_1 \cdot v_2}{\Vert v_1 \Ver