【多变量分析艺术】：高级卡方检验处理复杂数据关系

# 1. 多变量分析艺术简介

在数据分析的复杂世界中，多变量分析是一种强大的工具，它可以帮助我们理解和解释变量之间的相互关系。在这一章节中，我们将概述多变量分析的基础知识和其在数据探索中的重要性。多变量分析不仅仅是一种单一的分析方法，而是一个包含多个技术的广泛领域，它允许研究者同时考虑多个输入变量，并探索它们如何共同作用于一个或多个输出变量。

我们会首先介绍多变量分析的定义和它在现代数据分析实践中的应用背景，然后逐步深入到各种多变量分析方法的类型，例如线性回归、逻辑回归、主成分分析(PCA)以及因子分析等。这一章节的目标是为读者提供一个多变量分析的概览，为后续章节中更具体的技术讨论建立基础。我们会关注多变量分析在不同领域（如医学、社会科学和市场研究）中的实际应用，以及它如何在复杂数据集的解析中起到关键作用。

通过本章的学习，读者将能够理解多变量分析的核心概念，并意识到其在解释复杂数据关系中的重要价值。这为后续章节中针对特定方法，例如卡方检验的更深入探讨，奠定了坚实的基础。

# 2. 卡方检验基础理论

卡方检验作为统计学中一种非常重要的非参数检验方法，广泛应用于分类数据的分析，尤其是在探索两个分类变量之间是否存在独立性时显得尤为重要。本章节将深入探讨卡方检验的统计学原理、主要类型以及其统计意义，为读者提供一个全面且深入的卡方检验入门知识。

## 2.1 卡方检验的统计学原理

### 2.1.1 卡方分布的特点和适用条件

卡方分布是一种由多个独立的标准正态分布变量的平方和所形成的概率分布。其形状取决于自由度，随着自由度的增加，卡方分布会逐渐向正态分布靠近。卡方分布的适用条件通常包括数据的独立性和随机性，以及每个格子的期望频数不能太小，一般建议大于5。

**代码展示：**

# 使用R语言中的rchisq函数生成具有不同自由度的卡方分布数据
degrees_of_freedom <- c(1, 3, 5, 10, 20) # 自由度数组
x <- seq(0, 25, length=100) # 定义x轴的值

# 绘制不同自由度的卡方分布图
plot(x, dchisq(x, df=degrees_of_freedom[1]), type="l", col="red", ylim=c(0, 0.2),
     ylab="Density", main="Chi-Squared Distribution for Different Degrees of Freedom")
lines(x, dchisq(x, df=degrees_of_freedom[2]), type="l", col="blue")
lines(x, dchisq(x, df=degrees_of_freedom[3]), type="l", col="green")
lines(x, dchisq(x, df=degrees_of_freedom[4]), type="l", col="purple")
lines(x, dchisq(x, df=degrees_of_freedom[5]), type="l", col="orange")
legend(15, 0.2, legend=paste("df =", degrees_of_freedom),
       col=c("red", "blue", "green", "purple", "orange"), lty=1)

**逻辑分析及参数说明：**
在上面的代码中，我们使用了`rchisq`函数生成了具有不同自由度的卡方分布数据，并使用`plot`函数绘制了它们的密度函数图像。红色、蓝色、绿色、紫色、橙色分别对应了自由度为1、3、5、10、20的卡方分布。从图像中可以看出，自由度越大，卡方分布越接近正态分布，其形状也越来越平缓。在实际应用中，当自由度较大时，卡方分布可作为正态分布的一个近似。

### 2.1.2 卡方检验的假设基础

卡方检验建立在两个基本假设之上：一是数据的独立性，二是数据的随机性。数据的独立性指的是每个样本的观察结果不受其他样本影响；数据的随机性则意味着样本是从一个大的总体中随机抽取的，样本中的每个个体都有相同的概率被抽中。

- **独立性**：在卡方检验中，我们通常假设观察的两个变量是独立的。例如，在进行两个分类变量的独立性检验时，我们会检查这两个变量是否有相同的频率分布，即它们是否独立。
- **随机性**：随机性假设意味着数据的收集没有系统偏差，样本是从目标总体中随机抽取的，以保证样本的代表性。

## 2.2 卡方检验的主要类型

### 2.2.1 卡方拟合优度检验

卡方拟合优度检验用于检验观察频数与理论频数之间是否存在显著差异。例如，假设我们抛硬币100次，我们期望正面出现的次数接近50次，如果结果与期望有显著差异，卡方拟合优度检验将帮助我们确定这一差异是否只是偶然发生的。

**代码展示：**

# 示例：检验硬币抛掷的公平性
observed <- c(head=50, tails=50) # 观察到的频数
expected <- c(head=50, tails=50) # 理论上的期望频数

# 卡方拟合优度检验
chisq.test(x=observed, p=expected/sum(expected))

**逻辑分析及参数说明：**
在进行卡方拟合优度检验时，我们首先定义了观察频数`observed`和理论频数`expected`。接着，使用`chisq.test`函数对数据进行检验。这里我们假设抛硬币是公平的，即理论上正面和反面出现的次数应该是均等的。输出结果包括卡方值、自由度以及p值，可以告诉我们观察频数与理论频数之间是否存在显著差异。

### 2.2.2 卡方独立性检验

卡方独立性检验用于检验两个分类变量之间是否独立。比如，研究性别和喜欢某种产品的倾向是否存在某种统计意义上的相关性。

**代码展示：**

# 示例：检验性别与喜欢某种产品倾向之间的关系
contingency_table <- matrix(c(20, 30, 40, 10), nrow=2, byrow=TRUE)
dimnames(contingency_table) <- list(Gender=c("Male", "Female"), Product=c("Yes", "No"))

# 卡方独立性检验
chisq.test(contingency_table)

**逻辑分析及参数说明：**
在上述示例中，我们创建了一个2x2的列联表`contingency_table`，表示不同性别对于是否喜欢某种产品的偏好。然后使用`chisq.test`函数进行卡方独立性检验。输出结果将告诉我们两个分类变量之间是否存在统计学上的独立性。

### 2.2.3 卡方同质性检验

卡方同质性检验用于检验多个样本是否来自相同的总体分布。比如，研究不同地区的人们对于某个品牌的偏好是否相同。

**代码展示：**

# 示例：检验三个地区对于某品牌产品的偏好是否相同
three地区的偏好 <- matrix(c(50, 60, 55, 30, 40, 35), nrow=3, byrow=TRUE)
dimnames(three地区的偏好) <- list(Region=c("A", "B", "C"), Preference=c("Like", "Dislike"))

# 卡方同质性检验
chisq.test(three地区的偏好)

**逻辑分析及参数说明：**
在这个例子中，我们设计了一个3x2的列联表`three地区的偏好`，包含了三个地区关于是否喜欢某种产品的情况。通过`chisq.test`函数进行卡方同质性检验，结果将揭示不同地区之间是否存在显著的偏好差异。

## 2.3 卡方检验的统计意义

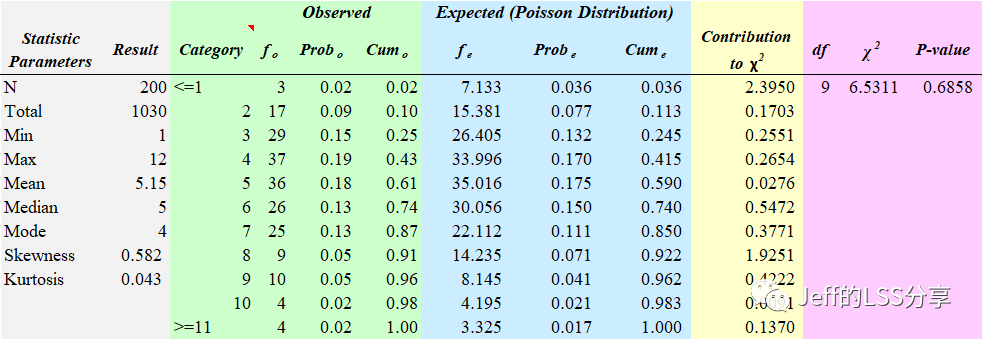
### 2.3.1 理论频率与实际频率的比较

卡方检验的核心在于比较观察到的数据（实际频率）和在零假设成立的情况下预期得到的数据（理论频率）。卡方值是实际频率与理论频率之间差异的度量，反映了观察数据与期望数据之间的偏差程度。

**代码展示：**

# 创建一个观测频数数据框
observed_frequencies <- data.frame(
  Category = c("A", "B", "C"),
  Frequency = c(25, 35, 40)
)

# 假设理论频率（期望频数）
expected_frequencies <- data.frame(
  Category = c("A", "B", "C"),
  Frequency =