【MATLAB图像处理中的均值滤波】：揭秘图像降噪的利器，轻松消除噪声，提升图像质量

# 1. MATLAB图像处理概述

MATLAB是一个强大的技术计算语言，在图像处理领域有着广泛的应用。图像处理涉及对图像进行各种操作，以增强其质量、提取信息或进行分析。MATLAB提供了一系列图像处理函数，使研究人员和工程师能够高效地执行这些操作。

本教程将重点介绍MATLAB图像处理的基础知识，从图像获取和预处理到图像增强和分析。我们将探讨各种图像处理技术，包括滤波、变换和分割，并通过实际示例展示它们的应用。本教程旨在为初学者和有经验的MATLAB用户提供一个全面且实用的指南，帮助他们掌握图像处理的基本原理和技术。

# 2. 均值滤波理论基础

### 2.1 均值滤波的原理和优点

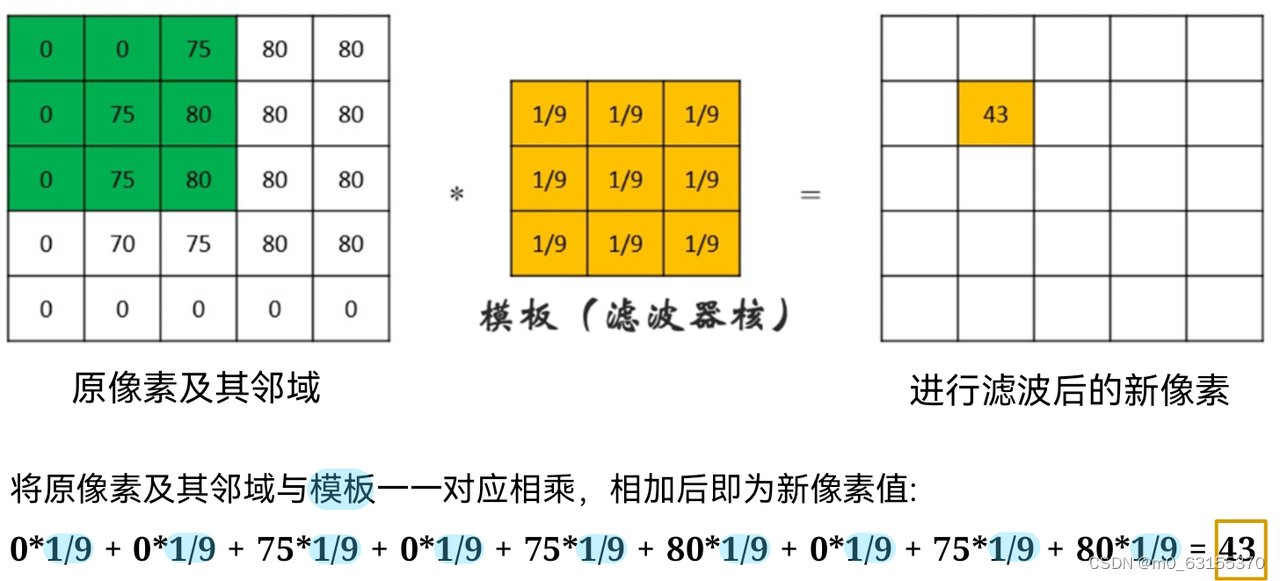
均值滤波是一种图像处理技术，用于通过计算图像中每个像素周围邻域像素的平均值来平滑图像。其基本原理是：

- 对于图像中的每个像素，创建一个以该像素为中心的方形邻域（称为滤波器）。
- 计算邻域内所有像素值的平均值。
- 将平均值替换为邻域中心像素的新值。

均值滤波的主要优点包括：

- **降噪：**均值滤波可以通过平均邻域像素值来抑制噪声，从而平滑图像。
- **图像平滑：**均值滤波还可以通过去除图像中的细小细节来平滑图像，从而使其看起来更加均匀。
- **计算简单：**均值滤波算法简单易于实现，计算成本低。

### 2.2 均值滤波的算法实现

均值滤波算法的伪代码如下：

for each pixel in the image:
    create a square neighborhood centered at the pixel
    calculate the average value of all pixels in the neighborhood
    replace the value of the center pixel with the average value

MATLAB 中实现均值滤波的代码如下：

% 读入图像
image = imread('noisy_image.jpg');

% 创建滤波器大小
filter_size = 3;

% 创建均值滤波器
filter = ones(filter_size, filter_size) / (filter_size^2);

% 应用均值滤波
filtered_image = imfilter(image, filter);

% 显示原图和滤波后的图像
subplot(1,2,1);
imshow(image);
title('Original Image');

subplot(1,2,2);
imshow(filtered_image);
title('Mean Filtered Image');

**代码逻辑分析：**

- `imread` 函数读取图像文件并将其存储在 `image` 变量中。
- `filter_size` 变量指定滤波器的尺寸（以像素为单位）。
- `ones` 函数创建一个填充 1 的矩阵，该矩阵的大小为 `filter_size` x `filter_size`。
- `imfilter` 函数应用均值滤波器 `filter` 到图像 `image`，并将结果存储在 `filtered_image` 变量中。
- `imshow` 函数显示原始图像和滤波后的图像。

# 3. 均值滤波实践应用

### 3.1 图像降噪示例

#### 3.1.1 噪声图像的获取和预处理

图像降噪是均值滤波的一个重要应用场景。为了演示均值滤波的降噪效果，我们首先需要获取一张含有噪声的图像。可以使用以下代码从网上获取一张自然图像：

% 获取图像 URL
image_url = 'https://upload.wikimedia.org/wikipedia/commons/thumb/e/ea/Toucan_from_the_Amazon_Rainforest_in_Tambopata_National_Reserve_Peru.jpg/1200px-Toucan_from_the_Amazon_Rainforest_in_Tambopata_National_Reserve_Peru.jpg';

% 下载并读取图像
image = imread(image_url);

% 添加高斯噪声
noise_level = 0.1;
noise = noise_level * randn(size(image));
noisy_image = image + noise;

执行上述代码后，`noisy_image` 中将包含一张含有高斯噪声的图像。

#### 3.1.2 均值滤波的应用和效果对比

接下来，我们可以使用均值滤波来去除噪声。以下代码演示了均值滤波的应用过程：

% 创建均值滤波器
filter_size = 3;
h = ones(filter_size) / (filter_size^2);

% 应用均值滤波
filtered_image = imfilter(noisy_image, h);

执行代码后，`filtered_image` 中将包含经过均值滤波处理的图像。

为了对比均值滤波前后图像的差异，我们可以使用以下代码进行可视化：

% 显示原始图像、噪声图像和滤波后图像
subplot(1, 3, 1);
imshow(image);
title('原始图像');

subplot(1, 3, 2);
imshow(noisy_image);
title('噪声图像');

subplot(1, 3, 3);
imshow(filtered_image);
title('均值滤波后图像');

执行代码后，将在同一窗口中显示原始图像、噪声图像和均值滤波后的图像，方便进行对比。

### 3.2 图像平滑示例

#### 3.2.1 图像平滑的必要性和目标

图像平滑是均值滤波的另一个重要应用场景。图像平滑可以去除图像中的高频噪声，从而使图像变得更加平滑。

#### 3.2.2 均值滤波在图像平滑中的应用

均值滤波是一种常用的图像平滑方法。通过对图像中的每个像素及其邻域像素进行平均，均值滤波可以有效去除高频噪声，同时保留图像中的重要特征。

以下代码演示了均值滤波在图像平滑中的应用过程：

% 创建图像
image = imread('image.jpg');

% 创建均值滤波器
filter_size = 5;
h = ones(filter_size) / (filter_size^2);

% 应用均值滤波
filtered_image = imfilter(image, h);

执行代码后，`filtered_image` 中将包含经过均值滤波处理的平滑图像。

为了对比均值滤波前后图像的差异，我们可以使用以下代码进行可视化：

% 显示原始图像和滤波后图像
subplot(1, 2, 1);
imshow(image);
title('原始图像');

subplot(1, 2, 2);
imshow(filtered_image);
title('均值滤波后图像');

执行代码后，将在同一窗口中显示原始图像和均值滤波后的平滑图像，方便进行对比。

# 4. 均值滤波参数优化

### 4.1 滤波器尺寸的选择

#### 4.1.1 滤波器尺寸对降噪效果的影响

滤波器尺寸是均值滤波的一个关键参数，它直接影响着滤波效果。滤波器尺寸越大，平滑效果越明显，但同时也会导致图像细节的损失。

考虑以下图像降噪示例：

% 原始噪声图像
original_image = imread('noisy_image.png');

% 不同滤波器尺寸的均值滤波
filtered_image1 = imfilter(original_image, fspecial('average', 3));
filtered_image2 = imfilter(original_image, fspecial('average', 5));
filtered_image3 = imfilter(original_image, fspecial('average', 7));

% 显示不同滤波器尺寸的滤波效果
figure;
subplot(1, 4, 1); imshow(original_image); title('原始图像');
subplot(1, 4, 2); imshow(filtered_image1); title('滤波器尺寸 3');
subplot(1, 4, 3); imshow(filtered_image2); title('滤波器尺寸 5');
subplot(1, 4, 4); imshow(filtered_image3); title('滤波器尺寸 7');

从上图中可以看出，随着滤波器尺寸的增加，图像中的噪声逐渐被平滑，但图像细节也逐渐丢失。

#### 4.1.2 滤波器尺寸的优化策略

选择合适的滤波器尺寸需要根据图像的具体情况进行权衡。一般来说，对于噪声较大的图像，可以使用较大的滤波器尺寸来获得更好的降噪效果。而对于细节丰富的图像，则需要使用较小的滤波器尺寸来保留图像细节。

### 4.2 边界处理方式

#### 4.2.1 边界处理对滤波效果的影响

在进行均值滤波时，需要考虑图像边界的处理方式。不同的边界处理方式会影响滤波效果，特别是图像边缘区域的处理。

考虑以下图像平滑示例：

% 原始图像
original_image = imread('image.png');

% 不同边界处理方式的均值滤波
filtered_image1 = imfilter(original_image, fspecial('average', 3), 'replicate');
filtered_image2 = imfilter(original_image, fspecial('average', 3), 'symmetric');
filtered_image3 = imfilter(original_image, fspecial('average', 3), 'circular');

% 显示不同边界处理方式的滤波效果
figure;
subplot(1, 4, 1); imshow(original_image); title('原始图像');
subplot(1, 4, 2); imshow(filtered_image1); title('复制边界');
subplot(1, 4, 3); imshow(filtered_image2); title('对称边界');
subplot(1, 4, 4); imshow(filtered_image3); title('循环边界');

从上图中可以看出，不同的边界处理方式对图像边缘区域的处理效果不同。复制边界会复制图像边缘的像素值，对称边界会对称地镜像图像边缘的像素值，而循环边界会将图像边缘的像素值循环地连接起来。

#### 4.2.2 常见的边界处理方法

常见的边界处理方法有：

* **复制边界 (replicate)**：复制图像边缘的像素值。
* **对称边界 (symmetric)**：对称地镜像图像边缘的像素值。
* **循环边界 (circular)**：将图像边缘的像素值循环地连接起来。
* **零边界 (zero)**：将图像边缘的像素值设置为 0。
* **反射边界 (reflect)**：将图像边缘的像素值反射到图像内部。

选择合适的边界处理方式需要根据图像的具体情况进行考虑。对于边缘区域比较重要的图像，可以使用对称边界或循环边界来保留边缘信息。而对于边缘区域不重要的图像，可以使用复制边界或零边界来简化计算。

# 5. 均值滤波与其他滤波器的比较

### 5.1 高斯滤波

**5.1.1 高斯滤波的原理和特点**

高斯滤波是一种线性平滑滤波器，它使用高斯函数作为滤波核。高斯函数是一个钟形曲线，其中心点权重最大，随着距离中心的增加，权重逐渐减小。

高斯滤波的公式如下：

G(x, y) = (1 / (2πσ^2)) * e^(-(x^2 + y^2) / (2σ^2))

其中：

* G(x, y) 是高斯滤波器的输出
* σ 是标准差，控制滤波器的平滑程度

高斯滤波具有以下特点：

* **平滑效果好：**高斯滤波器可以有效地去除图像中的噪声和细节，同时保持图像的边缘和轮廓。
* **无振铃效应：**高斯滤波器不会产生振铃效应，即在图像的边缘处出现不自然的明暗条纹。
* **计算复杂度高：**高斯滤波器的计算复杂度比均值滤波器高，因为需要计算高斯函数的卷积。

### 5.1.2 均值滤波与高斯滤波的比较

均值滤波和高斯滤波都是平滑滤波器，但它们在原理和效果上存在一些差异：

| 特征 | 均值滤波 | 高斯滤波 |
|---|---|---|
| 滤波核 | 均匀的矩形 | 高斯函数 |
| 平滑效果 | 较弱 | 较强 |
| 振铃效应 | 可能出现 | 不出现 |
| 计算复杂度 | 低 | 高 |

**应用场景：**

* 均值滤波适用于去除图像中的椒盐噪声和高斯噪声。
* 高斯滤波适用于去除图像中的高频噪声和保持图像的边缘和轮廓。

### 5.2 中值滤波

**5.2.1 中值滤波的原理和特点**

中值滤波是一种非线性平滑滤波器，它使用图像中像素的局部中值作为滤波器的输出。中值滤波的公式如下：

M(x, y) = median(S(x, y))

其中：

* M(x, y) 是中值滤波器的输出
* S(x, y) 是滤波器窗口内的像素集合

中值滤波具有以下特点：

* **抗噪性强：**中值滤波器可以有效地去除图像中的椒盐噪声和脉冲噪声。
* **边缘保持性好：**中值滤波器不会模糊图像的边缘和轮廓。
* **计算复杂度高：**中值滤波器的计算复杂度比均值滤波器和高斯滤波器都高，因为需要对滤波器窗口内的像素进行排序。

### 5.2.2 均值滤波与中值滤波的比较

均值滤波和中值滤波都是平滑滤波器，但它们在原理和效果上存在一些差异：

| 特征 | 均值滤波 | 中值滤波 |
|---|---|---|
| 滤波核 | 均匀的矩形 | 局部像素的中值 |
| 平滑效果 | 较弱 | 较强 |
| 边缘保持性 | 较差 | 较好 |
| 抗噪性 | 较弱 | 较强 |
| 计算复杂度 | 低 | 高 |

**应用场景：**

* 均值滤波适用于去除图像中的高斯噪声和随机噪声。
* 中值滤波适用于去除图像中的椒盐噪声和脉冲噪声，并保持图像的边缘和轮廓。

# 6. 均值滤波在图像处理中的应用拓展

### 6.1 图像增强

#### 6.1.1 均值滤波在图像增强中的应用

均值滤波除了用于图像降噪和平滑外，还可以应用于图像增强。图像增强旨在改善图像的视觉效果，使其更易于理解和分析。均值滤波可以通过调节滤波器尺寸和边界处理方式来实现图像增强。

#### 6.1.2 实际案例：图像对比度增强

以下是一个使用均值滤波增强图像对比度的实际案例：

% 读取图像
image = imread('low_contrast.jpg');

% 创建均值滤波器
h = fspecial('average', [5 5]);

% 应用均值滤波
filtered_image = imfilter(image, h);

% 显示原始图像和增强后的图像
subplot(1,2,1);
imshow(image);
title('原始图像');

subplot(1,2,2);
imshow(filtered_image);
title('增强对比度的图像');

在这个示例中，我们使用了一个 5x5 的均值滤波器对低对比度的图像进行滤波。滤波后的图像对比度明显增强，细节更加清晰。

### 6.2 图像分割

#### 6.2.1 均值滤波在图像分割中的作用

均值滤波在图像分割中也发挥着重要作用。图像分割旨在将图像划分为不同的区域或对象。均值滤波可以帮助平滑图像，消除噪声，从而 облегчить последующую сегментацию.

#### 6.2.2 实际案例：图像分割中的区域生长

以下是一个使用均值滤波辅助图像分割的实际案例：

% 读取图像
image = imread('segmented_image.jpg');

% 应用均值滤波
filtered_image = imfilter(image, fspecial('average', [3 3]));

% 进行区域生长分割
segmented_image = imsegment(filtered_image);

% 显示原始图像和分割后的图像
subplot(1,2,1);
imshow(image);
title('原始图像');

subplot(1,2,2);
imshow(segmented_image);
title('分割后的图像');

在这个示例中，我们使用了一个 3x3 的均值滤波器对图像进行预处理。预处理后的图像噪声减少，区域边界更加清晰。随后，我们使用区域生长算法对图像进行分割，得到了较好的分割结果。