MATLAB图像平均值处理：图像增强与降噪的利器

# 1. 图像平均值处理概述**

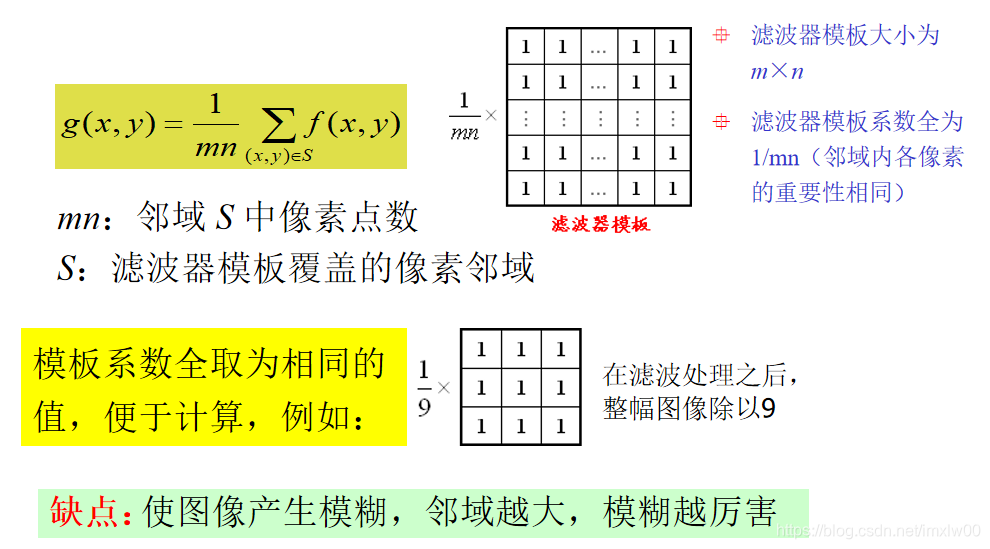
图像平均值处理是一种图像处理技术，它通过计算图像中每个像素周围邻域像素的平均值来平滑图像。这种技术广泛用于图像增强和降噪，因为它可以有效去除噪声和模糊图像细节。

平均值滤波的原理很简单：对于图像中的每个像素，计算其周围邻域内所有像素的平均值，并用该平均值替换原始像素值。邻域的大小和形状可以根据所需的平滑程度进行调整。

# 2. 图像平均值处理的理论基础

### 2.1 图像平均值滤波的原理

图像平均值滤波是一种图像处理技术，通过计算图像中每个像素周围邻域内像素值的平均值，来平滑图像并减少噪声。其基本原理如下：

对于图像中的每个像素 `p`，其周围邻域内 `n` 个像素的平均值滤波结果 `p'` 定义为：

p' = (1/n) * ∑(q ∈ N(p)) q

其中：

* `N(p)` 表示像素 `p` 的邻域，通常为一个正方形或圆形区域。
* `q` 表示 `N(p)` 中的像素。

### 2.2 平均值滤波器的设计与实现

平均值滤波器的设计主要涉及邻域大小和形状的选择。常用的邻域形状包括正方形、圆形和高斯核。

**正方形邻域：**

正方形邻域是最简单的邻域类型，其形状为正方形，邻域大小由正方形边长决定。

**圆形邻域：**

圆形邻域的形状为圆形，其大小由圆的半径决定。圆形邻域的优点是其对图像边缘的处理效果较好。

**高斯核：**

高斯核是一种权重函数，其形状为钟形曲线。高斯核的中心权重最大，随着距离中心的增加，权重逐渐减小。高斯核可以有效地抑制噪声，同时保持图像的边缘信息。

平均值滤波器的实现可以使用卷积操作。卷积操作将滤波器内核与图像进行逐像素的乘法和累加，得到滤波后的结果。

**代码块：**

% 定义正方形邻域
square_kernel = ones(3, 3) / 9;

% 定义圆形邻域
radius = 2;
[x, y] = meshgrid(-radius:radius, -radius:radius);
circle_kernel = exp(-(x.^2 + y.^2) / (2 * radius^2)) / (2 * pi * radius^2);

% 定义高斯核
sigma = 1;
[x, y] = meshgrid(-3 * sigma:3 * sigma, -3 * sigma:3 * sigma);
gaussian_kernel = exp(-(x.^2 + y.^2) / (2 * sigma^2)) / (2 * pi * sigma^2);

% 应用滤波器
filtered_image = conv2(image, square_kernel, 'same');
filtered_image = conv2(image, circle_kernel, 'same');
filtered_image = conv2(image, gaussian_kernel, 'same');

**代码逻辑分析：**

* `ones(3, 3) / 9` 创建一个 3x3 的正方形内核，每个元素的值为 1/9。
* `meshgrid(-radius:radius, -radius:radius)` 创建一个以原点为中心的半径为 `radius` 的网格。
* `exp(-(x.^2 + y.^2) / (2 * radius^2)) / (2 * pi * radius^2)` 计算圆形内核的权重函数。
* `conv2(image, kernel, 'same')` 使用卷积操作将滤波器内核应用于图像。`'same'` 参数指定输出图像的大小与输入图像相同。

# 3. 图像平均值处理的实践应用

### 3.1 图像去噪

图像去噪是图像处理中的一项重要任务，其目的是去除图像中的噪声，提高图像质量。图像平均值处理是图像去噪的常用方法之一，它通过计算图像中每个像素点的邻域平均值来平滑图像，从而去除噪声。

#### 3.1.1 均值滤波

均值滤波是最简单的图像平均值滤波方法，它通过计算图像中每个像素点周围邻域的平均值来平滑图像。均值滤波的优点是计算简单，实现容易。但是，均值滤波也会导致图像细节的丢失，尤其是边缘和纹理细节。

% 均值滤波
I = imread('noisy_image.jpg');
filtered_image = imfilter(I, ones(3, 3) / 9);
% 显示原始图像和去噪后的图像
figure;
subplot(1, 2, 1);
imshow(I);
title('原始图像');
subplot(1, 2, 2);
imshow(filtered_image);
title('均值滤波后的图像');

**代码逻辑分析：**

* `imread('noisy_image.jpg')`：读取噪声图像。
* `imfilter(I, ones(3, 3) / 9)`：使用 3x3 的均值滤波器对图像进行滤波。
* `figure`：创建新的图形窗口。
* `subplot(1, 2, 1)`：将图形窗口分成两列，并选择第一列。
* `imshow(I)`：显示原始图像。
* `title('原始图像')`：设置原始图像的标题。
* `subplot(1, 2, 2)`：选择第二列。
* `imshow(filtered_image)`：显示去噪后的图像。
* `title('均值滤波后的图像')`：设置去噪后图像的标题。

#### 3.1.2 高斯滤波

高斯滤波是一种改进的均值滤波方法，它使用高斯核来计算图像中每个像素点的邻域平均值。高斯核是一种钟形函数，其中心权重最大，边缘权重逐渐减小。因此，高斯滤波可以更好地保留图像的边缘和纹理细节，同时去除噪声。

% 高斯滤波
I = imread('noisy_image.jpg');
filtered_image = imgaussfilt(I, 2);
% 显示原始图像和去噪后的图像
figure;
subplot(1, 2, 1);
imshow(I);
title('原始图像');
subplot(1, 2, 2);
imshow(filtered_image);
title('高斯滤波后的图像');

**代码逻辑分析：**

* `imread('noisy_image.jpg')`：读取噪声图像。
* `imgaussfilt(I, 2)`：使用标准差为 2 的高斯核对图像进行滤波。
* `figure`：创建新的图形窗口。
* `subplot(1, 2, 1)`：将图形窗口分成两列，并选择第一列。
* `imshow(I)`：显示原始图像。
* `title('原始图像')`：设置原始图像的标题。
* `subplot(1, 2, 2)`：选择第二列。
* `imshow(filtered_image)`：显示去噪后的图像。
* `title('高斯滤波后的图像')`：设置去噪后图像的标题。

### 3.2 图像增强

图像增强是图像处理中另一项重要任务，其目的是改善图像的视觉效果，使其更易于理解和分析。图像平均值处理也可以用于图像增强，通过调整图像的对比度和锐度来改善其视觉效果。

#### 3.2.1 对比度增强

对比度增强可以改善图像中不同区域之间的亮度差异，使其更易于区分。图像平均值处理可以通过计算图像中每个像素点周围邻域的平均值和方差来增强对比度。

% 对比度增强
I = imread('low_contrast_image.jpg');
filtered_image = imadjust(I, [0.2 0.8], []);
% 显示原始图像和增强后的图像
figure;
subplot(1, 2, 1);
imshow(I);
title('原始图像');
subplot(1, 2, 2);
imshow(filtered_image);
title('对比度增强后的图像');

**代码逻辑分析：**

* `imread('low_contrast_image.jpg')`：读取低对比度图像。
* `imadjust(I, [0.2 0.8], [])`：调整图像的对比度，将最低值映射到 0.2，最高值映射到 0.8。
* `figure`：创建新的图形窗口。
* `subplot(1, 2, 1)`：将图形窗口分成两列，并选择第一列。
* `imshow(I)`：显示原始图像。
* `title('原始图像')`：设置原始图像的标题。
* `subplot(1, 2, 2)`：选择第二列。
* `imshow(filtered_image)`：显示增强后的图像。
* `title('对比度增强后的图像')`：设置增强后图像的标题。

#### 3.2.2 锐化

锐化可以增强图像中边缘和纹理的清晰度，使其更易于识别。图像平均值处理可以通过计算图像中每个像素点周围邻域的梯度来锐化图像。

% 锐化
I = imread('blurred_image.jpg');
filtered_image = imsharpen(I, 'Amount', 1);
% 显示原始图像和锐化后的图像
figure;
subplot(1, 2, 1);
imshow(I);
title('原始图像');
subplot(1, 2, 2);
imshow(filtered_image);
title('锐化后的图像');

**代码逻辑分析：**

* `imread('blurred_image.jpg')`：读取模糊图像。
* `imsharpen(I, 'Amount', 1)`：锐化图像，将锐化量设置为 1。
* `figure`：创建新的图形窗口。
* `subplot(1, 2, 1)`：将图形窗口分成两列，并选择第一列。
* `imshow(I)`：显示原始图像。
* `title('原始图像')`：设置原始图像的标题。
* `subplot(1, 2, 2)`：选择第二列。
* `imshow(filtered_image)`：显示锐化后的图像。
* `title('锐化后的图像')`：设置锐化后图像的标题。

# 4. 图像平均值处理的进阶应用**

**4.1 多尺度平均值滤波**

多尺度平均值滤波是一种将图像分解为不同尺度的子带，并对每个子带应用平均值滤波的方法。它可以有效地处理不同尺度的噪声和纹理。

**4.1.1 金字塔分解**

金字塔分解是一种将图像分解为不同尺度的子带的方法。它使用一系列低通滤波器和抽样操作来创建金字塔结构。

% 图像金字塔分解
[pyr, pind] = buildpyr(image, 'auto', 5);

**4.1.2 图像融合**

图像融合是将不同尺度的子带融合成一幅图像的过程。它可以用来去除噪声或增强纹理。

% 图像融合
fusedImage = pyrrecon(pyr, pind);

**4.2 非线性平均值滤波**

非线性平均值滤波是一种对图像中的每个像素应用非线性函数的平均值滤波方法。它可以有效地去除噪声和保留边缘。

**4.2.1 中值滤波**

中值滤波是一种非线性平均值滤波方法，它将每个像素替换为其邻域中像素的中值。

% 中值滤波
filteredImage = medfilt2(image, [3 3]);

**4.2.2 双边滤波**

双边滤波是一种非线性平均值滤波方法，它考虑了像素之间的空间距离和像素值的相似性。

% 双边滤波
filteredImage = imguidedfilter(image, 'NeighborhoodSize', [5 5], 'DegreeOfSmoothing', 0.1);

**代码逻辑分析：**

* `buildpyr`函数使用低通滤波器和抽样操作将图像分解为金字塔结构。
* `pyrrecon`函数将不同尺度的子带融合成一幅图像。
* `medfilt2`函数将每个像素替换为其邻域中像素的中值。
* `imguidedfilter`函数考虑了像素之间的空间距离和像素值的相似性来进行滤波。

**参数说明：**

* `buildpyr`函数的参数：
* `image`：输入图像。
* `'auto'`: 自动选择滤波器和分解层数。
* `5`: 分解层数。
* `pyrrecon`函数的参数：
* `pyr`: 金字塔结构。
* `pind`: 金字塔索引。
* `medfilt2`函数的参数：
* `image`: 输入图像。
* `[3 3]`: 滤波器大小。
* `imguidedfilter`函数的参数：
* `image`: 输入图像。
* `'NeighborhoodSize'`: 邻域大小。
* `'DegreeOfSmoothing'`: 平滑程度。

# 5. MATLAB中图像平均值处理的实现

### 5.1 基本函数与操作

MATLAB提供了丰富的图像处理函数，其中与平均值处理相关的函数包括：

- `imfilter`: 用于对图像应用各种滤波器，包括平均值滤波。
- `fspecial`: 用于创建各种滤波器核，包括平均值滤波器。
- `imnoise`: 用于向图像添加噪声，以便测试去噪算法。
- `imshow`: 用于显示图像，以便可视化处理结果。

### 5.2 滤波器设计与应用

要设计平均值滤波器，可以使用`fspecial`函数。例如，创建一个3x3的平均值滤波器：

h = fspecial('average', 3);

要将滤波器应用于图像，可以使用`imfilter`函数。例如，对图像`I`应用平均值滤波：

I_filtered = imfilter(I, h);

### 5.3 图像增强与降噪实例

**图像去噪**

平均值滤波可用于去除图像中的噪声。例如，使用平均值滤波器对噪声图像进行去噪：

% 添加噪声到图像
I_noisy = imnoise(I, 'gaussian', 0.1);

% 应用平均值滤波去噪
I_denoised = imfilter(I_noisy, h);

% 显示去噪后的图像
imshow(I_denoised);

**图像增强**

平均值滤波还可用于增强图像。例如，使用平均值滤波器增强图像的对比度：

% 创建一个对比度增强滤波器
h_contrast = fspecial('unsharp', 0.5);

% 应用滤波器增强对比度
I_enhanced = imfilter(I, h_contrast);

% 显示增强后的图像
imshow(I_enhanced);