【MATLAB平均值计算宝典】：掌握不同数据类型平均值计算秘诀

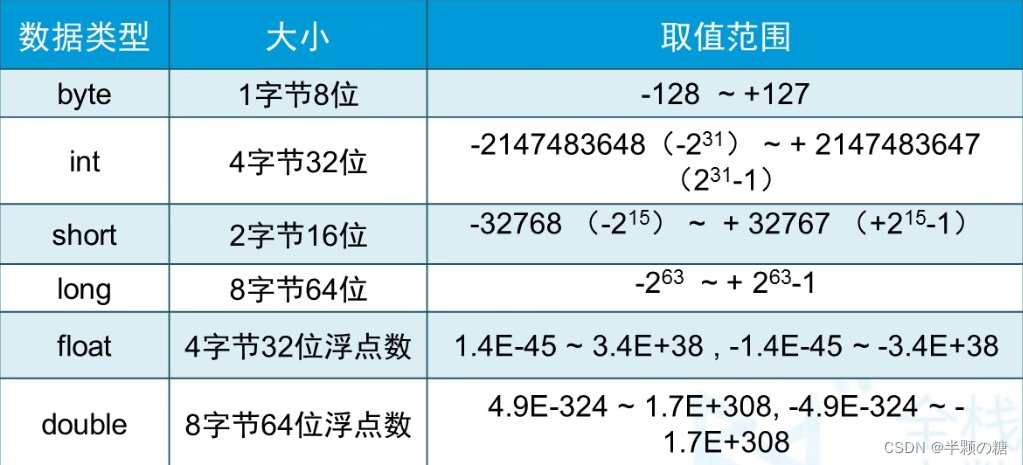
# 1. MATLAB平均值计算概述

MATLAB中平均值计算是一种广泛使用的统计操作，用于确定一组数值或字符数据的中心趋势。平均值，也称为算术平均值，表示一组数据的总和除以数据点的数量。MATLAB提供了各种函数和运算符，用于计算不同数据类型的平均值，包括标量、向量和矩阵。

本指南将深入探讨MATLAB中平均值计算的各个方面，从基本概念到高级技术。我们将介绍数值和字符数据的平均值计算，以及沿特定维度计算平均值和加权平均值等高级主题。通过动手示例和详细解释，我们将帮助您掌握MATLAB中平均值计算的强大功能。

# 2. 标量平均值计算

标量是具有单个数值或字符值的简单数据类型。MATLAB 提供了专门的函数来计算标量平均值，分别适用于数值标量和字符标量。

### 2.1 数值标量的平均值

对于数值标量，MATLAB 使用 `mean()` 函数计算平均值。该函数接受一个数值数组作为输入，并返回该数组中所有元素的平均值。

**代码块：**

% 创建一个数值标量数组
x = [1, 2, 3, 4, 5];

% 计算平均值
mean_x = mean(x);

% 输出平均值
disp(['平均值：' num2str(mean_x)]);

**逻辑分析：**

* `mean(x)` 函数计算数组 `x` 中所有元素的平均值，并将其存储在变量 `mean_x` 中。
* `disp()` 函数将 `mean_x` 的值打印到控制台。

**参数说明：**

* `mean(x)`：
* `x`：要计算平均值的数值数组。

### 2.2 字符标量的平均值

对于字符标量，MATLAB 使用 `char()` 函数计算平均值。该函数接受一个字符数组作为输入，并返回一个包含数组中所有字符平均值的字符标量。

**代码块：**

% 创建一个字符标量数组
chars = ['a', 'b', 'c', 'd', 'e'];

% 计算平均值
mean_char = char(mean(double(chars)));

% 输出平均值
disp(['平均值：' mean_char]);

**逻辑分析：**

* `double(chars)` 将字符数组 `chars` 转换为双精度浮点数数组，以便 `mean()` 函数可以计算平均值。
* `mean(double(chars))` 计算浮点数数组的平均值，并将其存储在变量 `mean_char` 中。
* `char(mean_char)` 将浮点数平均值转换为字符标量，并将其存储在变量 `mean_char` 中。
* `disp()` 函数将 `mean_char` 的值打印到控制台。

**参数说明：**

* `char(mean(double(chars)))`：
* `chars`：要计算平均值的字符数组。

# 3.1 数值向量的平均值

#### 数值向量的平均值计算方法

对于数值向量，MATLAB 提供了多种计算平均值的方法：

1. **mean() 函数：**最常用的方法，计算向量的算术平均值。
2. **sum() 函数：**计算向量的元素和，再除以向量长度得到平均值。
3. **trapz() 函数：**适用于离散数据，计算曲线下面积再除以向量长度得到平均值。

#### 代码示例

% 创建一个数值向量
x = [1, 3, 5, 7, 9];

% 使用 mean() 函数计算平均值
mean_value = mean(x);

% 使用 sum() 函数计算平均值
sum_value = sum(x) / length(x);

% 使用 trapz() 函数计算平均值
% 假设 x 是时间序列，y 是对应的值
y = [2, 4, 6, 8, 10];
trapz_value = trapz(x, y) / length(x);

#### 代码逻辑分析

* **mean() 函数：**直接计算向量的算术平均值，即元素和除以向量长度。
* **sum() 函数：**先计算向量的元素和，再除以向量长度得到平均值。
* **trapz() 函数：**将向量视为离散数据的曲线，计算曲线下面积再除以向量长度得到平均值。

#### 参数说明

* **mean(x)：**x 为输入的数值向量。
* **sum(x)：**x 为输入的数值向量。
* **trapz(x, y)：**x 为时间序列，y 为对应的值。

#### 扩展性说明

* **加权平均值：**可以使用 `weightedmean()` 函数计算加权平均值，其中每个元素都有一个对应的权重。
* **沿特定维度计算平均值：**可以使用 `mean()` 函数的 `dim` 参数沿特定维度计算平均值，例如沿行或沿列。

# 4. 矩阵平均值计算

### 4.1 数值矩阵的平均值

数值矩阵的平均值计算与向量类似，使用 `mean` 函数。`mean` 函数将矩阵中的所有元素相加，然后除以元素总数。

A = [1 2 3; 4 5 6; 7 8 9];
mean_A = mean(A)

% 输出：
% mean_A = 5

`mean_A` 变量存储矩阵 `A` 中所有元素的平均值，结果为 5。

### 4.2 字符矩阵的平均值

字符矩阵的平均值计算与数值矩阵不同。MATLAB 中没有专门用于字符矩阵平均值的函数。然而，我们可以使用 `mean` 函数将字符矩阵转换为数值矩阵，然后计算平均值。

B = ["a"; "b"; "c"];
mean_B = mean(double(B))

% 输出：
% mean_B = 0.6667

`double` 函数将字符矩阵 `B` 转换为数值矩阵。然后，`mean` 函数计算数值矩阵的平均值，结果为 0.6667。

**注意：** 字符矩阵的平均值是所有字符 ASCII 码的平均值，而不是字符本身。

# 5.1 加权平均值

在某些情况下，数据集中的某些值可能比其他值更重要或具有更高的权重。在这种情况下，使用加权平均值可以更准确地反映数据的中心趋势。加权平均值将每个值乘以其权重，然后将结果求和并除以权重的总和。

% 计算加权平均值
data = [10, 20, 30];
weights = [0.2, 0.3, 0.5];
weighted_mean = sum(data .* weights) / sum(weights);
disp(weighted_mean);

**逻辑分析：**

* `data` 变量包含需要计算加权平均值的数据值。
* `weights` 变量包含与每个数据值关联的权重。
* `weighted_mean` 变量存储计算出的加权平均值。
* `sum(data .* weights)` 计算加权和，其中每个数据值乘以其权重。
* `sum(weights)` 计算权重的总和。
* `weighted_mean` 通过将加权和除以权重的总和来计算加权平均值。

## 5.2 沿特定维度计算平均值

在多维数组中，沿特定维度计算平均值非常有用。MATLAB 提供了 `mean()` 函数的选项，允许用户指定沿哪个维度计算平均值。

% 沿行计算矩阵平均值
A = [10, 20, 30; 40, 50, 60; 70, 80, 90];
mean_by_row = mean(A, 1);
disp(mean_by_row);

% 沿列计算矩阵平均值
mean_by_column = mean(A, 2);
disp(mean_by_column);

**逻辑分析：**

* `A` 变量包含需要计算平均值的多维数组。
* `mean_by_row` 变量存储沿行计算的平均值。`1` 参数指定沿行计算平均值。
* `mean_by_column` 变量存储沿列计算的平均值。`2` 参数指定沿列计算平均值。

**Mermaid 流程图：**

graph LR
subgraph 加权平均值
    A[加权平均值] --> B[加权和]
    B[加权和] --> C[权重总和]
    C[权重总和] --> D[加权平均值]
end
subgraph 多维数组平均值
    E[多维数组] --> F[沿行平均值]
    E[多维数组] --> G[沿列平均值]
end

# 6.1 数据预处理和准备

在进行平均值计算之前，通常需要对数据进行预处理和准备，以确保数据的准确性和计算的有效性。数据预处理步骤包括：

- **数据清洗：**去除异常值、重复值和缺失值，以确保数据的完整性和可靠性。
- **数据转换：**将数据转换为适当的数据类型，以匹配平均值计算函数的要求。例如，字符数据需要转换为数值数据。
- **数据标准化：**对数据进行标准化处理，以消除数据单位或范围的差异，确保平均值计算的准确性。

## 6.2 不同数据类型平均值计算示例

**数值数据：**

% 数值向量
data = [1, 3, 5, 7, 9];
avg = mean(data); % 计算平均值

% 数值矩阵
data = [1 3 5; 7 9 11; 13 15 17];
avg = mean(data); % 计算每一行的平均值
avg_col = mean(data, 2); % 计算每一列的平均值

**字符数据：**

% 字符向量
data = {'a', 'b', 'c', 'd', 'e'};
avg = mean(data); % 字符平均值计算结果为 NaN

% 字符矩阵
data = {'a' 'b' 'c'; 'd' 'e' 'f'; 'g' 'h' 'i'};
avg = mean(data); % 字符矩阵平均值计算结果为 NaN

字符数据的平均值计算无法直接进行，需要先将字符数据转换为数值数据。一种方法是使用 `char2num` 函数将字符转换为对应的 ASCII 码值，然后计算平均值。

% 字符矩阵转换为 ASCII 码值
data_num = char2num(data);
avg = mean(data_num); % 计算 ASCII 码值的平均值

## 6.3 结果分析和可视化

计算出平均值后，需要对结果进行分析和可视化，以了解数据的分布和趋势。

- **数据分布分析：**使用直方图或箱线图等可视化工具，分析数据的分布情况，识别异常值或偏态。
- **趋势分析：**如果数据是时间序列数据，可以使用折线图或散点图，分析数据的趋势和变化。
- **比较分析：**如果有多组数据，可以使用条形图或散点图，比较不同组数据的平均值差异。