MATLAB平均值聚类：揭示数据中的相似性和差异性

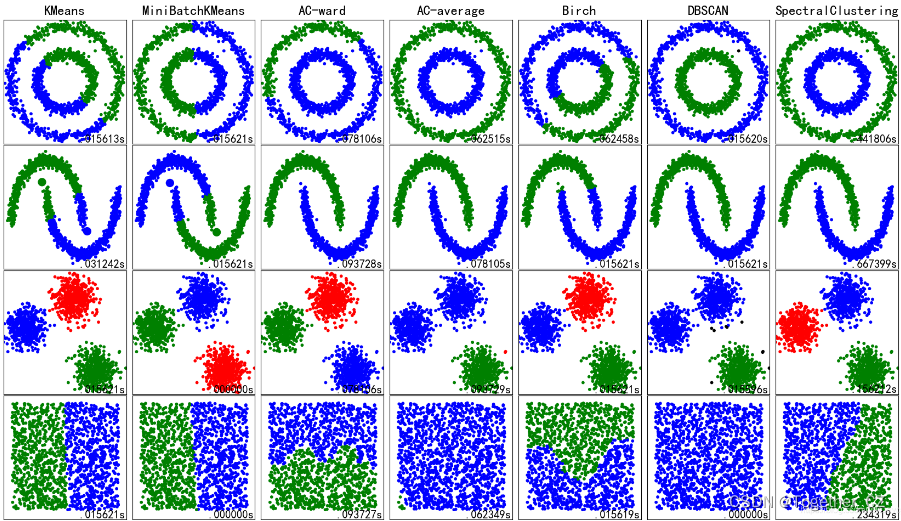
# 1. 聚类分析概述

聚类分析是一种无监督机器学习技术，用于识别数据中的相似性和差异性，将具有相似特征的数据点分组到不同的簇中。聚类分析广泛应用于各种领域，如客户细分、文本挖掘和图像处理。

聚类分析算法有多种，平均值聚类是最常用的算法之一。平均值聚类算法通过迭代地将数据点分配到最近的簇中心来工作，并不断更新簇中心，直到达到收敛。平均值聚类算法简单易懂，并且在处理大数据集时效率很高。

# 2. MATLAB中平均值聚类算法**

## 2.1 平均值聚类的原理和过程

平均值聚类是一种基于距离的聚类算法，它将数据点分配到簇中，使得每个簇中数据点的平均值与簇中心之间的距离最小。平均值聚类算法的步骤如下：

1. **初始化：**将每个数据点作为单独的簇。
2. **计算距离：**计算每个簇中所有数据点之间的距离。
3. **合并：**找到距离最小的两个簇，并将它们合并为一个新的簇。
4. **更新：**计算新簇的中心。
5. **重复：**重复步骤 2-4，直到达到预定的簇数或满足停止条件。

## 2.2 MATLAB中实现平均值聚类的方法

MATLAB中提供了 `kmeans` 函数来实现平均值聚类算法。`kmeans` 函数的语法如下：

[idx, C, sumd, D] = kmeans(X, k)

其中：

* `X`：输入数据，每一行表示一个数据点。
* `k`：簇的数目。
* `idx`：每个数据点所属的簇索引。
* `C`：每个簇的中心。
* `sumd`：每个数据点到其所属簇中心的距离平方和。
* `D`：每个数据点到所有簇中心的距离矩阵。

**代码示例：**

% 生成一些数据
data = rand(100, 2);

% 使用平均值聚类算法将数据聚类为 3 个簇
[idx, C] = kmeans(data, 3);

% 绘制聚类结果
figure;
scatter(data(:, 1), data(:, 2), 100, idx, 'filled');
title('平均值聚类结果');

**代码逻辑分析：**

* `rand(100, 2)` 生成一个 100 行 2 列的随机数据矩阵。
* `kmeans(data, 3)` 使用 `kmeans` 函数将数据聚类为 3 个簇，并返回每个数据点所属的簇索引和每个簇的中心。
* `scatter(data(:, 1), data(:, 2), 100, idx, 'filled')` 根据数据点的位置和所属的簇索引绘制散点图，并使用不同的颜色填充不同的簇。

## 2.3 平均值聚类参数的设置

平均值聚类算法的参数设置对聚类结果有很大的影响。最重要的参数是：

* **簇数 (k)：**这是聚类算法需要确定的主要参数。选择合适的簇数取决于数据的性质和聚类的目的。
* **距离度量：**平均值聚类算法使用距离度量来计算数据点之间的距离。常用的距离度量包括欧几里得距离、曼哈顿距离和余弦相似度。
* **最大迭代次数：**这是算法在终止之前可以执行的迭代次数的最大值。
* **终止条件：**算法可以在满足某些条件时终止，例如当聚类结果不再发生显著变化时。

**参数优化：**

为了优化平均值聚类算法的参数，可以采用以下方法：

* **肘部法则：**绘制簇数与聚类误差（例