Scipy新手速成：安装、配置和操作全攻略

# 1. Scipy简介与安装流程

## 1.1 Scipy简介

Scipy是一个开源的Python算法库和数学工具包，它在NumPy基础上提供了许多用于科学计算的工具。Scipy包含多个子模块，如优化、插值、线性代数、傅里叶变换等，适用于各种科学领域，包括物理、工程、生物学、金融和更多。它的功能强大，能够执行复杂的数据分析和处理，是数据科学家和工程师的得力工具。

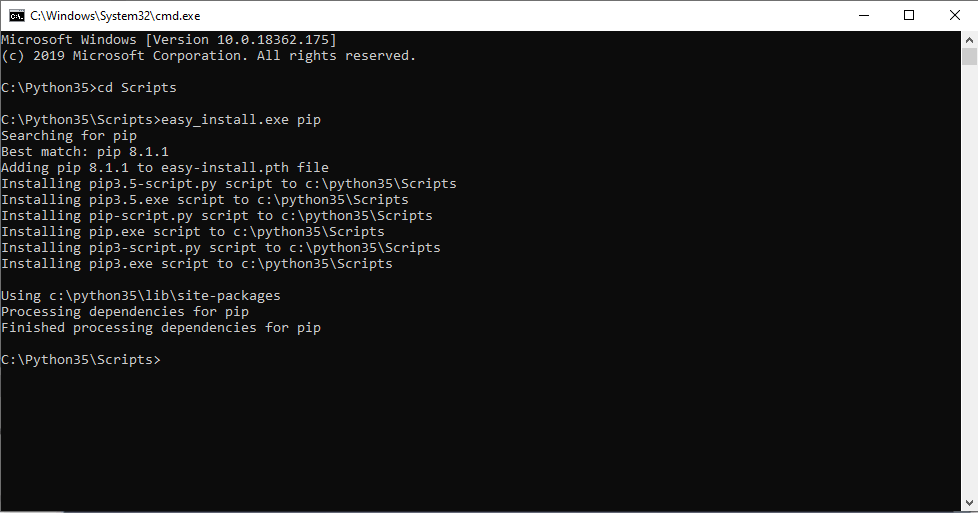
## 1.2 Scipy的安装流程

安装Scipy非常简单，如果你已经安装了Python和pip，只需打开命令行工具，执行以下指令：

pip install scipy

对于某些特定需求，可能需要预先安装其他依赖库，如BLAS或LAPACK，但一般来说，pip安装过程会自动处理这些依赖关系。如果在安装过程中遇到任何问题，可以查看官方文档或者搜索相关错误信息来解决。安装完成后，你可以通过以下Python代码来检查Scipy是否成功安装：

import scipy
print(scipy.__version__)

如果看到版本号输出，则表示Scipy已安装成功，可以开始你的科学计算之旅。

# 2. Scipy基础操作指南

## 2.1 Scipy核心库的导入和使用
### 2.1.1 导入库的基本方法

在使用Scipy进行科学计算之前，首先需要导入Scipy库。Scipy是一个开源的Python算法库和数学工具包，它基于Numpy构建，提供了许多用于科学和工程计算的模块。导入Scipy库的常用方法是在Python脚本或交互式会话的开始处使用`import`语句。

下面是一个导入Scipy库的基本示例：

import scipy

然而，这种导入方式只能访问Scipy的顶级命名空间。为了便于使用，更常见的做法是使用别名`sp`来导入Scipy，这样可以减少键入的工作量，提高代码的可读性。

import scipy as sp

或者，我们还可以选择性地导入Scipy中的特定模块或函数，例如：

from scipy import linalg, optimize

这样，我们就可以直接使用`linalg`和`optimize`模块中的函数，而无需通过Scipy的前缀。

### 2.1.2 常用函数和模块的概述

Scipy包含多个子模块，每个模块都针对特定的科学计算领域。以下是一些最常用的Scipy模块及其功能概述：

- `scipy.integrate`: 用于数值积分和常微分方程求解。
- `scipy.optimize`: 提供了函数最小化、非线性方程求解等优化算法。
- `scipy.linalg`: 扩展了Numpy的线性代数功能，包括矩阵分解等。
- `scipy.signal`: 用于信号处理和滤波器设计。
- `scipy.stats`: 包含了统计学函数和概率分布。

在使用特定函数之前，了解其功能和参数是必要的。例如，如果你想进行数值积分，`scipy.integrate.quad`函数是一个不错的选择：

result, error = sp.integrate.quad(lambda x: sp.sin(x)/x, 0, sp.inf)

在上述代码中，`quad`函数计算了一个无穷区间上正弦函数除以其变量的积分，并返回积分的结果`result`和估计误差`error`。

通过上述例子，我们可以看出，Scipy使得复杂的数学计算变得简单和直观。在下面的章节中，我们将深入探讨如何使用Scipy进行矩阵和数组操作，以及统计学功能的运用。

## 2.2 矩阵和数组操作
### 2.2.1 创建和修改数组

在Scipy中，数组的操作通常依赖于Numpy库，因为Scipy主要是在Numpy的基础上提供了更高级的数学函数。创建数组是进行科学计算的第一步，Numpy提供了一系列函数来创建数组，例如`np.zeros`、`np.ones`、`np.arange`和`np.linspace`等。

这里我们举例展示如何创建一个数组：

import numpy as np

# 创建一个长度为10的数组，其元素全部是0
array_zero = np.zeros(10)

# 创建一个长度为10的数组，其元素全部是1
array_one = np.ones(10)

# 创建一个从0到9的数组
array_range = np.arange(10)

# 创建一个在0到1之间等间隔的10个数的数组
array_linspace = np.linspace(0, 1, 10)

修改数组时，可以直接对数组进行索引或切片，以便进行赋值或进行元素级的运算。

# 修改数组中的元素
array_zero[0] = 1
array_zero[1:] = 2

# 用另一个数组替换数组的一部分
array_zero[2:5] = array_linspace[:3]

### 2.2.2 矩阵运算基础

在Scipy中，`scipy.linalg`模块提供了丰富的线性代数运算功能。创建矩阵的一种常见方法是使用`np.array`或`np.matrix`，后者的用法更适合进行矩阵运算。

以下是如何创建矩阵并进行基本运算的示例：

# 创建两个矩阵
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

# 矩阵乘法
C = np.dot(A, B)

# 矩阵求逆
inv_A = sp.linalg.inv(A)

在Scipy中，`linalg`模块还提供了计算特征值和特征向量、矩阵分解等功能。

### 2.2.3 线性代数的高级操作

高级操作包括但不限于矩阵的特征值问题、奇异值分解、矩阵函数等。这些操作往往在解决实际问题中扮演着重要角色。

以下是一个特征值问题的示例：

# 计算矩阵A的特征值和特征向量
eigenvalues, eigenvectors = sp.linalg.eig(A)

在这个例子中，`eig`函数计算矩阵A的特征值和特征向量，它们在物理系统、动态系统分析以及许多其他应用领域中非常重要。

下表总结了Scipy在矩阵和数组操作中常用的函数和方法：

| 函数/方法 | 用途 |
| ------------------ | ------------------------------------------------------------ |
| `np.zeros` | 创建一个指定大小的全零数组 |
| `np.ones` | 创建一个指定大小的全一数组 |
| `np.arange` | 创建一个等间隔的数值数组 |
| `np.linspace` | 创建一个在指定范围内等间隔的数值数组 |
| `np.dot` | 计算两个数组或矩阵的点积（对矩阵而言为矩阵乘法） |
| `sp.linalg.inv` | 计算矩阵的逆 |
| `sp.linalg.eig` | 计算矩阵的特征值和特征向量 |

在本章后续部分，我们将详细讨论统计学功能的运用，这是Scipy在数据分析中非常重要的一个方面。

## 2.3 统计学功能的运用
### 2.3.1 数据的分布和抽样

统计学是研究数据收集、分析、解释和呈现的科学。Scipy提供了广泛的统计学功能，这些功能可以帮助我们更好地理解和分析数据。从数据分布到抽样，Scipy的`scipy.stats`模块可以处理各种统计问题。

数据分布是统计学的基础概念之一。在Scipy中，我们可以使用`scipy.stats`中的分布对象来生成随机变量，并评估概率密度、累积分布函数等。

from scipy.stats import norm

# 创建一个正态分布的随机变量实例
rv = norm(loc=0, scale=1)  # loc为均值，scale为标准差

# 生成一组服从该分布的随机数
data = rv.rvs(size=1000)

在上面的代码中，我们首先创建了一个均值为0，标准差为1的正态分布实例。然后，使用`rvs`方法生成了1000个服从该分布的随机数样本。

### 2.3.2 假设检验和置信区间

假设检验是统计学中的一个重要概念，用来检验对总体参数的某种假设是否成立。Scipy的`stats`模块包含多种检验函数，如t检验、卡方检验等。

假设我们要检验两个样本的均值是否存在显著差异。我们可以使用t检验来完成这个任务：

from scipy.stats import ttest_ind

# 假设有两组样本数据
group1 = [2.9, 3.0, 2.5, 2.6]
group2 = [3.2, 3.3, 3.4, 3.0]

# 进行独立样本t检验
t_stat, p_value = ttest_ind(group1, group2)

print('t统计量:', t_stat)
print('p值:', p_value)

此外，我们还可以计算数据的置信区间。置信区间是总体参数的一个区间估计，它表示我们对参数值落在该区间的信心程度。

# 计算均值的95%置信区间
ci = norm.interval(0.95, loc=np.mean(data), scale=norm.std(data) / np.sqrt(len(data)))
print('均值的95%置信区间:', ci)

在上述代码中，我们使用了正态分布的`interval`方法来计算数据均值的95%置信区间。

通过Scipy进行假设检验和置信区间计算，可以有效地帮助我们对数据进行推断统计分析。在接下来的章节中，我们将探讨如何将这些基础操作应用于实际的数据处理实践中。

# 3. Scipy数据处理实践

在上一章中，我们对Scipy库的基本结构和基础操作有了初步的了解。现在，让我们深入Scipy在数据处理中的实际应用，掌握如何使用Scipy进行数据的输入输出处理、数据清洗和预处理，以及数据的可视化。

## 3.1 数据输入输出处理

### 3.1.1 读写不同格式的数据文件

Scipy提供了多种函数来处理数据输入输出，可以轻松地读写常见的数据文件格式。包括但不限于CSV、文本文件、MATLAB文件、HDF5文件等。

import scipy.io as sio

# 保存数据为Matlab文件
sio.savemat('data.mat', {'arr': np.array([[1, 2], [3, 4]])})

# 读取Matlab文件
mat = sio.loadmat('data.mat')
print(mat['arr'])

该代码块展示了如何保存一个NumPy数组到一个Matlab格式的文件中，以及如何再次加载这个文件并提取数据。需要注意的是，`loadmat`函数返回的是一个字典对象，键是变量名，值是对应的变量内容。

### 3.1.2 数据的导入导出技巧

在实际工作中，经常会涉及到从外部数据源导入数据，或是将处理好的数据导出到外部文件中。以下是将Pandas DataFrame导出到CSV文件，然后从CSV文件读取回DataFrame的过程：

import pandas as pd
import scipy.io

# 创建一个简单的DataFrame
df = pd.DataFrame({
    'A': [1, 2, 3],
    'B': [4, 5, 6]
})

# 导出DataFrame到CSV文件
df.to_csv('data.csv', index=False)

# 从CSV文件读取数据到DataFrame
new_df = pd.read_csv('data.csv')
print(new_df)

在这个例子中，`to_csv`方法将DataFrame导出到CSV文件，`index=False`参数确保在文件中不包含行索引。随后，`read_csv`方法被用来读取数据并创建一个新的DataFrame对象。

## 3.2 数据清洗和预处理

数据的清洗和预处理是数据分析中非常关键的步骤。它决定了后续分析的准确性和效率。

### 3.2.1 缺失值处理

在现实世界的数据集中，缺失值是很常见的问题。我们可以使用Scipy中的函数来识别和处理这些缺失值。

import numpy as np

# 创建一个包含缺失值的数组
data = np.array([[1, 2, np.nan], [np.nan, 3, 4]])

# 填充缺失值
data_filled = np.nan_to_num(data, copy=True, nan=0.0)

print(data_filled)

在上面的代码中，我们使用`np.nan_to_num`函数将数组中的`np.nan`值替换为0.0。`copy=True`参数确保我们不会修改原始数据。

### 3.2.2 数据标准化和归一化

数据标准化和归一化是常见的数据预处理技术，它们可以帮助改善算法的性能和收敛速度。

from sklearn.preprocessing import StandardScaler, MinMaxScaler

# 创建一个数据集
data = np.array([[1, 2], [3, 4], [5, 6]])

# 标准化数据
scaler_standard = StandardScaler().fit(data)
data_standard = scaler_standard.transform(data)

# 归一化数据
scaler_minmax = MinMaxScaler().fit(data)
data_minmax = scaler_minmax.transform(data)

# 打印处理后的数据
print("标准化后的数据:")
print(data_standard)
print("\n归一化后的数据:")
print(data_minmax)

在这段代码中，我们使用了`sklearn.preprocessing`模块中的`StandardScaler`和`MinMaxScaler`类对数据进行标准化和归一化。这些方法非常适合在机器学习中处理特征数据。

### 3.2.3 数据的转换和编码

在处理分类数据时，我们经常需要将非数值型数据转换成数值型，以便于算法处理。

from sklearn.preprocessing import LabelEncoder

# 示例数据
labels = ['red', 'green', 'blue', 'green', 'red']

# 创建编码器，并拟合数据
encoder = LabelEncoder()
encoded_labels = encoder.fit_transform(labels)

print("编码后的标签:")
print(encoded_labels)

上述代码使用了`LabelEncoder`来对颜色标签进行编码，将其转换为数值。在实际应用中，这样的技术非常适用于处理标签数据。

## 3.3 数据可视化

数据可视化是传达数据含义的直观方式，Scipy支持基本的绘图功能，但更复杂的可视化任务可以借助Matplotlib或Seaborn库来完成。

### 3.3.1 基本的绘图功能介绍

Scipy使用`scipy.stats`模块提供了一些基本的绘图函数，例如绘制直方图、箱型图等。

import scipy.stats as stats

# 生成一些正态分布的随机数据
data = stats.norm.rvs(size=1000)

# 绘制直方图
stats.probplot(data, dist="norm", plot=plt)
plt.show()

上述代码使用`stats.probplot`函数绘制了数据的正态概率图，这有助于验证数据是否符合正态分布。

### 3.3.2 高级图表的定制与展示

要创建高级图表，我们常常需要使用其他库。在此，提供一个使用Matplotlib创建散点图和线图的例子：

import matplotlib.pyplot as plt

# 创建一些散点数据
x = np.random.normal(0, 1, 100)
y = np.random.normal(0, 1, 100)

# 绘制散点图
plt.scatter(x, y)

# 绘制线图
plt.plot(x, y, color='red')

plt.title('散点图和线图')
plt.xlabel('X轴')
plt.ylabel('Y轴')
plt.show()

在这个例子中，`scatter`函数用来绘制散点图，而`plot`函数用来在同一个图中添加线图。通过`plt.title`, `plt.xlabel`, 和`plt.ylabel`可以自定义图表的标题和坐标轴标签。

在本章节中，我们介绍了如何使用Scipy以及相关库进行数据的输入输出处理、数据清洗和预处理以及数据的可视化。掌握这些技能对于进行高效的数据分析至关重要。接下来，在第四章中，我们将探索Scipy在科学计算中的应用，包括微积分运算、优化、插值和拟合技术，以及特殊函数和常数的应用。

# 4. Scipy在科学计算中的应用

在本章节中，我们将深入探讨Scipy库在科学计算领域的应用，这些应用广泛且多样，是科研和工程计算中不可或缺的工具。Scipy不仅提供了大量的算法和函数，还与NumPy等其他库紧密集成，为处理科学计算问题提供了强大的支持。

## 4.1 微积分运算和优化

微积分运算和优化是科学计算中常见的需求，特别是在物理学、工程学、经济学等领域。Scipy库通过其`integrate`和`optimize`模块，提供了丰富的函数来解决积分、微分、优化等问题。

### 4.1.1 积分和微分运算基础

积分和微分是微积分中的基本运算，它们在求解物理问题、优化问题和模拟动态系统时有着广泛的应用。Scipy的`integrate`模块包含了用于执行这些操作的函数。

积分运算可以分为定积分和不定积分。Scipy提供了`quad`函数用于数值计算定积分，而`odeint`函数则用于求解常微分方程初值问题。例如：

from scipy import integrate

# 定积分计算示例
def integrand(x):
    return x**2

result, error = integrate.quad(integrand, 0, 1)
print(f"定积分的结果是：{result}，误差估计为：{error}")

在上述代码中，`quad`函数接受两个参数：一个是要积分的函数，另一个是积分的上下限。执行后，`result`变量中存储了积分的计算结果，而`error`变量中存储了估计误差。

对于微分运算，Scipy同样提供了多种求解方法。使用`diff`函数可以进行数值微分计算。

### 4.1.2 优化问题的求解方法

在科学研究和工程设计中，优化问题无处不在，例如设计最优的材料结构、寻找成本最低的生产方案等。Scipy的`optimize`模块集成了多种优化算法，可以用来求解线性和非线性优化问题。

以最小化函数为例，可以使用`minimize`函数，它支持多种优化算法：

from scipy.optimize import minimize

# 定义待最小化的目标函数
def objective_function(x):
    return x[0]**2 + x[1]**2

# 初始猜测值
x0 = [1.3, 0.7]

# 调用minimize函数进行最小化
result = minimize(objective_function, x0)

print(f"最小化结果：\n{result}")

在这个例子中，我们定义了一个简单的二次函数作为目标函数，并给出了初始猜测值。执行`minimize`函数后，返回一个包含最优解、目标函数值等信息的结果对象。

## 4.2 插值和拟合技术

在科学和工程领域，经常需要从一组离散的数据点中推断出函数关系或趋势，插值和拟合技术便是解决这一问题的关键。

### 4.2.1 插值算法的原理与应用

插值是根据一组离散的数据点，构造一个新的函数来逼近这些数据点的过程。这在数据重建、信号处理等领域十分常见。Scipy的`interpolate`模块提供了多种插值算法，如`interp1d`用于一维插值，`griddata`用于多维插值。

下面给出一个一维插值的例子：

import numpy as np
from scipy import interpolate

# 已知数据点
x_known = np.array([0, 1, 2, 3, 4, 5])
y_known = np.array([0, 0.8, 0.9, 0.1, -0.8, -1])

# 创建插值函数
linear_interpolation = interpolate.interp1d(x_known, y_known)

# 新的查询点
x_new = np.linspace(0, 5, 50)
y_new = linear_interpolation(x_new)

# 绘制插值结果
import matplotlib.pyplot as plt

plt.plot(x_known, y_known, 'o', label='已知数据点')
plt.plot(x_new, y_new, '-', label='插值结果')
plt.legend()
plt.show()

在上面的代码中，我们使用`interp1d`函数创建了一个插值函数`linear_interpolation`，该函数根据已知数据点`x_known`和`y_known`进行线性插值。然后，我们使用`linspace`函数生成了一组新的查询点，并用插值函数计算了这些点的插值结果。最后，我们使用matplotlib库绘制了已知数据点和插值结果。

### 4.2.2 数据拟合与曲线拟合技巧

与插值不同，拟合主要关注的是在给定数据点上找到最符合数据的函数模型。拟合过程中，模型参数是未知的，需要通过优化方法得到。Scipy的`curve_fit`函数可以实现曲线拟合，它基于非线性最小二乘法。

以下是一个简单的曲线拟合示例：

from scipy.optimize import curve_fit

# 定义拟合函数模型，y = a * exp(b * x)
def model(x, a, b):
    return a * np.exp(b * x)

# 已知的数据点
x_data = np.linspace(0, 4, 50)
y_data = model(x_data, 2.5, 1.3) + 0.2 * np.random.normal(size=x_data.size)

# 使用curve_fit进行参数拟合
params, covariance = curve_fit(model, x_data, y_data)

print(f"拟合得到的参数：a = {params[0]}, b = {params[1]}")

在这个例子中，`model`函数定义了我们想要拟合的模型，其中`a`和`b`是未知参数。使用`curve_fit`函数可以估计出这些参数，并通过最小化残差的平方和来得到最优解。

## 4.3 特殊函数和常数

在物理学和工程学中，经常使用到一些特殊的函数和常数。Scipy的`special`模块和`constants`模块提供了这些功能的实现，方便在科学计算中使用。

### 4.3.1 物理和工程学中的特殊函数

特殊函数在量子物理、电磁学、热力学等领域中有着广泛的应用。Scipy的`special`模块提供了包括贝塞尔函数、伽马函数、误差函数等在内的多种特殊函数。

例如，贝塞尔函数在圆形波导、热传导等物理问题中非常重要，Scipy的实现如下：

from scipy.special import jn  # jn代表第一类贝塞尔函数

# 计算不同阶数和不同自变量的贝塞尔函数值
x = np.linspace(0, 10, 50)
for n in range(4):
    y = jn(n, x)
    plt.plot(x, y, label=f'n={n}')

plt.legend()
plt.show()

在该代码中，我们计算了第一类贝塞尔函数的前四个阶数在一系列自变量下的值，并将它们绘制在一张图上。

### 4.3.2 常用数学常数的介绍与应用

在科学研究中，常用到如π、自然对数的底数e等数学常数。Scipy的`constants`模块中提供了一个丰富的常数集合，可以直接在计算中使用。

例如，获取圆周率π的值：

from scipy import constants

pi_value = constants.pi
print(f"圆周率π的值为：{pi_value}")

这些常数的使用简化了代码编写过程，并且避免了硬编码，使得科学计算更加准确和方便。

通过本章节的介绍，我们看到了Scipy库在微积分、插值和拟合、特殊函数等科学计算领域的强大功能。无论是处理复杂的数学问题，还是进行高效的算法实现，Scipy都是一个不可多得的工具。在接下来的章节中，我们将进一步探讨Scipy在机器学习中的应用，以及如何通过性能优化和扩展包来增强Scipy的计算能力。

# 5. Scipy与机器学习的结合

## 5.1 Scipy在机器学习中的角色

### 5.1.1 机器学习基础与Scipy的联系

机器学习领域与数据处理和数学运算密切相关，而Scipy作为一个强大的科学计算库，在机器学习的多个方面都扮演着关键角色。Scipy提供了大量数值计算工具，适用于数据预处理、特征提取、统计分析等多个环节。例如，在数据预处理环节，Scipy可以帮助我们进行数据的标准化、归一化以及缺失值处理等。在统计分析中，Scipy提供了描述统计功能，可以帮助我们理解数据的分布情况，为后续的机器学习模型建立提供数据洞察。

Scipy中的一些高级功能，如稀疏矩阵的支持和优化算法，也使得它成为构建和测试复杂机器学习算法的理想选择。Scipy中的`optimize`模块为优化问题提供了强大的工具，这些工具在特征选择、模型参数优化等机器学习任务中非常有用。

### 5.1.2 Scipy中的数据预处理工具

数据预处理是机器学习中不可或缺的一个环节，它直接影响到后续模型的性能。Scipy提供了一系列的工具，用于帮助我们进行有效的数据预处理。在数据标准化和归一化方面，Scipy的`stats`模块中的`zscore`函数可以用来计算标准分数，帮助数据进行标准化。数据的归一化可以使用`minmax_scale`函数进行。

对于缺失值的处理，虽然Scipy没有直接提供处理缺失值的函数，但是通过其基础数组操作，我们可以灵活地处理或替换掉这些缺失值。例如，可以使用数组切片、索引、条件表达式等方法来识别和替换缺失值。此外，Scipy还支持各种矩阵操作，比如稀疏矩阵的创建和操作，这对于处理大规模数据集和稀疏特征矩阵尤其有用。

## 5.2 特征提取与转换

### 5.2.1 特征提取的基本方法

特征提取是机器学习流程中的重要环节，它涉及到从原始数据中提取有用信息，形成模型训练所需的特征向量。在Scipy中，虽然没有直接的机器学习模型，但可以利用其强大的数值计算能力来实现一些基础的特征提取方法。

例如，利用Scipy的傅里叶变换（`scipy.fft`）可以提取时间序列数据的频率特征。另一个例子是使用主成分分析（PCA）方法来降维。虽然Scipy没有直接提供PCA函数，但可以通过其矩阵操作和线性代数函数来实现PCA的核心算法。

### 5.2.2 降维技术的应用

降维是一种常用的特征提取技术，旨在减少数据集的特征数量，同时尽量保留原始数据的重要信息。Scipy提供了两种主要的降维技术实现：特征选择和特征提取。

在特征选择方面，可以使用Scipy中的统计方法，比如相关系数计算，来评估特征与目标变量之间的关联性，从而选择与目标变量关系最强的特征。特征提取方法中，Scipy可以辅助实现一些线性降维方法，如线性判别分析（LDA）。

## 5.3 算法实现与评估

### 5.3.1 常见算法的Scipy实现

虽然Scipy主要是用于数值计算和科学运算，但它提供的工具也可以用于实现一些基础的机器学习算法。例如，k-means聚类算法可以通过Scipy中的`scipy.spatial.distance`来计算距离矩阵，然后利用迭代方法来更新聚类中心。对于线性回归等回归模型，可以使用Scipy中的优化模块来求解最小二乘问题。

### 5.3.2 模型评估与验证技巧

模型评估和验证是确保机器学习模型泛化能力的关键环节。Scipy中并没有直接的模型评估工具，但我们可以结合其优化方法和统计函数来评估模型性能。例如，使用交叉验证方法时，可以通过Scipy的`stats`模块来计算不同模型在不同折数上的评估指标（如R²、MAE、RMSE等），然后计算这些指标的均值和标准差来评估模型的稳定性和性能。

在这一过程中，可以使用Scipy提供的随机数生成器（`scipy.stats`）来生成训练集和测试集，从而对模型进行反复验证。此外，Scipy中的`permutation_test`函数可以用来进行统计检验，判断不同模型的差异是否显著。

# 6. Scipy高级话题与优化

在机器学习和数据分析领域，高效利用计算资源至关重要。Scipy库不仅提供了丰富的科学计算功能，还支持高性能计算的集成，同时也有着丰富的社区资源和扩展包供用户选择。在本章中，我们将深入探讨Scipy的高级话题与性能优化，并了解如何利用社区资源和扩展包来增强我们的项目。

## 6.1 高性能计算的集成

在处理大规模数据集和复杂算法时，传统的单线程计算模式往往难以满足性能需求。此时，高性能计算技术如并行计算与多线程、GPU加速成为了我们的解决方案。

### 6.1.1 并行计算与多线程

Scipy库通过其子库如`scipy.weave`、`scipy.spatial`和`scipy.integrate`提供了并行计算的支持。Python本身不是为并行计算设计的，因此在Scipy中，这通常是通过调用底层的多线程或多进程库来实现的。

from scipy import integrate
from scipy.weave import converters

def f(x):
    return x

# 使用Scipy的并行库进行积分计算
result = integrate.quad(f, 0, 1, threads=2) # 并行线程数设置为2

在上面的代码中，`integrate.quad`函数的`threads`参数允许我们指定并行线程的数量，从而加速计算过程。

### 6.1.2 GPU加速的应用

对于数值密集型的计算，如矩阵运算，利用GPU进行加速可以显著提高性能。虽然Scipy本身不直接支持GPU加速，但可以配合其他库如CuPy或者直接使用Numba、PyCUDA等进行GPU编程。

from numba import vectorize, float64

@vectorize([float64(float64)])
def add(a, b):
    return a + b

# 假设x和y是大型的浮点数数组
x = np.arange(1e7)
y = np.arange(1e7)

result = add(x, y)

在上面的示例中，我们使用Numba的`vectorize`装饰器将Python函数转换为向量化的GPU函数。

## 6.2 Scipy性能优化

当应用变得复杂时，性能瓶颈可能成为限制因素。识别和优化这些瓶颈是确保应用性能的关键。

### 6.2.1 性能分析与瓶颈识别

性能分析是识别程序性能瓶颈的过程。通常使用诸如`cProfile`这样的工具进行性能分析，然后使用`pstats`模块对结果进行分析。

import cProfile
from scipy import linalg

def compute_eigenvalues(matrix):
    return linalg.eigvals(matrix)

# 对特定函数进行性能分析
cProfile.run('compute_eigenvalues(np.random.rand(1000, 1000))')

在这个例子中，我们使用`cProfile`对求解矩阵特征值的函数`compute_eigenvalues`进行了性能分析。

### 6.2.2 优化策略和最佳实践

一旦识别出性能瓶颈，可以采取多种策略进行优化，包括但不限于选择更高效的算法、使用更高效的数据结构、减少不必要的计算和内存使用等。Scipy本身在设计时考虑到了性能因素，但用户也可以通过调整参数和合理选择函数来进一步优化性能。

## 6.3 社区资源与扩展包

Scipy背后有一个活跃的社区，不断推动其发展和完善。同时，也有许多第三方扩展包可以与Scipy无缝集成。

### 6.3.1 获取社区支持和贡献代码

Scipy的官方论坛和邮件列表是获取帮助和贡献代码的好地方。在社区里，用户可以提出问题、报告错误、提供代码优化建议，甚至参与Scipy的开发。

### 6.3.2 探索和使用扩展包

Scipy社区内有很多独立开发的扩展包，例如`statsmodels`和`pandas`。这些扩展包丰富了Scipy的功能，并针对特定领域进行了优化。

import pandas as pd

# 使用Pandas处理复杂的数据结构
df = pd.read_csv('data.csv')
df.groupby('category').mean()

在这个例子中，我们使用了Pandas库来读取CSV文件并进行数据分析。Pandas与Scipy完美结合，扩展了数据处理的能力。

随着技术的发展，Scipy不断地进化，它不仅提供了强大的科学计算工具，还通过集成高性能计算、提供社区支持和扩展包，帮助开发者解决实际问题。通过深入理解和应用Scipy的高级特性，我们可以显著提升开发和研究的效率。