MATLAB正切函数在信号处理中的应用：从理论到实践，掌握信号分析

# 1. 正切函数的数学基础

正切函数是三角函数中的一种，定义为对角线与邻边的比值。在数学中，正切函数通常表示为 tan(x)，其中 x 是输入角度。

正切函数的图像是一个周期性的曲线，其周期为 π。在 [0, π/2] 区间内，正切函数单调递增，在 [π/2, π] 区间内单调递减。正切函数在 x = π/2 处有垂直渐近线，在 x = 0, π, 2π, ... 处有零点。

# 2. 正切函数在信号处理中的理论应用

正切函数在信号处理中扮演着至关重要的角色，其独特的数学特性使其在滤波器设计、频谱分析和信号变换等领域得到了广泛的应用。本章将深入探讨正切函数在信号处理中的理论基础，为后续的实践应用奠定坚实的基础。

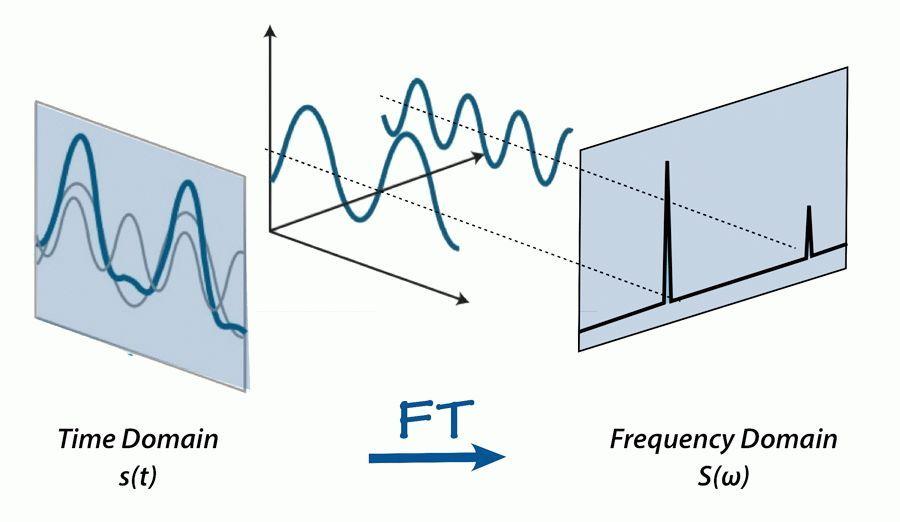
### 2.1 正切函数的频域特性

正切函数在时域和频域上都具有显著的特性。在时域上，正切函数是一个奇函数，具有对称性。而在频域上，正切函数的幅度响应具有带通特性，即在特定频率范围内具有较高的增益，而在其他频率范围内则衰减。

**代码块 1：正切函数的频域响应**

% 定义频率范围
f = linspace(-100, 100, 1000);

% 计算正切函数的频域响应
H = tan(f);

% 绘制幅度响应
figure;
plot(f, abs(H));
xlabel('频率 (Hz)');
ylabel('幅度');
title('正切函数的频域响应');

**逻辑分析：**

代码块 1 生成了一个频率范围，并计算了正切函数在该频率范围内的频域响应。绘制的幅度响应图显示了正切函数的带通特性，在低频和高频区域均衰减，而在特定频率范围内具有较高的增益。

### 2.2 正切函数在滤波器设计中的应用

正切函数的带通特性使其在滤波器设计中得到了广泛的应用。通过调整正切函数的带宽和中心频率，可以设计出满足特定要求的带通滤波器和带阻滤波器。

#### 2.2.1 带通滤波器设计

带通滤波器允许特定频率范围内的信号通过，而衰减其他频率范围的信号。正切函数的带通特性使其非常适合设计带通滤波器。

**代码块 2：带通滤波器设计**

% 定义滤波器参数
fc = 50; % 中心频率
bw = 20; % 带宽

% 设计正切带通滤波器
[b, a] = tan(fc, bw);

% 绘制滤波器响应
figure;
freqz(b, a);
xlabel('频率 (Hz)');
ylabel('幅度 (dB)');
title('正切带通滤波器响应');

**逻辑分析：**

代码块 2 使用 `tan` 函数设计了一个带通滤波器。`fc` 参数指定了滤波器的中心频率，`bw` 参数指定了滤波器的带宽。绘制的滤波器响应图显示了滤波器在中心频率附近具有较高的增益，而在其他频率范围内衰减。

#### 2.2.2 带阻滤波器设计

带阻滤波器允许特定频率范围内的信号通过，而衰减其他频率范围的信号。正切函数的带通特性使其通过反相操作也可以设计出带阻滤波器。

**代码块 3：带阻滤波器设计**

% 定义滤波器参数
fc = 50; % 中心频率
bw = 20; % 带宽

% 设计正切带阻滤波器
[b, a] = tan(fc, bw, 'notch');

% 绘制滤波器响应
figure;
freqz(b, a);
xlabel('频率 (Hz)');
ylabel('幅度 (dB)');
title('正切带阻滤波器响应');

**逻辑分析：**

代码块 3 使用 `tan` 函数设计了一个带阻滤波器。