Z-N法整定PID参数：故障诊断与快速解决控制问题的秘诀


# 摘要
PID控制器作为一种广泛使用的反馈控制器，其参数的正确整定对于确保控制系统的稳定性和响应速度至关重要。Z-N法作为一种经典而有效的方法，提供了基于经验公式的PID参数整定步骤和技巧。本文首先介绍PID控制理论基础，包括P、I、D的作用和PID控制方程的构成，然后详述Z-N法整定PID参数的步骤，包括确定临界增益和临界周期，以及如何使用Z-N公式进行参数计算。此外，本文还探讨了故障诊断和问题解决的策略，以及Z-N法与其他整定技术的比较，例如响应曲线法和现代智能算法的应用。本文的目标是为工程师提供一种系统的PID参数整定方法，提高他们处理控制问题的效率和效果。

# 关键字
Z-N法；PID控制器；系统性能；故障诊断；参数整定；控制策略

参考资源链接：[Z-N法整定PID参数经验分享](https://wenku.csdn.net/doc/6412b793be7fbd1778d4acb6?spm=1055.2635.3001.10343)
# 1. Z-N法整定PID参数简介

在自动化控制领域中，PID控制器是广泛使用的反馈回路控制器，它通过调节系统的输出以达到期望的性能。Z-N法（Ziegler-Nichols方法）是一种经典且实用的PID参数整定方法，以其简便性和有效性而闻名。本章将简要介绍Z-N法的起源、它在自动化领域中的应用以及为何它在工业控制中依然扮演着重要角色。

## 1.1 Z-N法的起源和背景

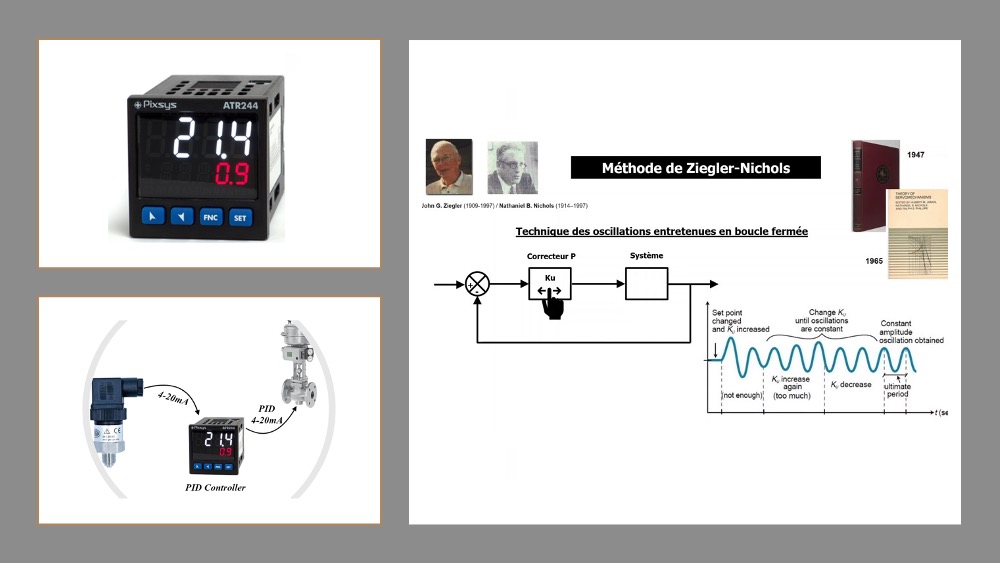
Z-N法由Ziegler和Nichols在20世纪40年代提出，其初衷是为了简化PID控制器参数的设置过程。在当时，控制器参数的调整主要依赖于工程师的经验，过程既复杂又耗时。Z-N法的提出为自动化控制的参数调整带来了革命性的简化，使得更多非专业人员也能快速有效地配置PID参数。

## 1.2 Z-N法在工业中的应用

随着工业自动化的发展，Z-N法已经成为一种标准的控制器参数整定方法。无论是在温度控制、速度调节，还是在位置跟踪系统中，Z-N法都能够提供一套快速得到性能良好控制器参数的准则。它的普及，极大地推动了自动化控制系统在工业中的广泛应用和效率提升。

## 1.3 Z-N法的现代意义

尽管现代控制系统引入了更多先进的整定技术，但Z-N法依然在许多场合保持着其重要地位。它的简便性和实用性使其在一些非关键场合或是用作初设参数时仍然非常受欢迎。同时，Z-N法也启发了后来许多更复杂控制算法的研究与发展。

随着本文的深入，我们将详细讨论PID控制理论基础，逐步解析Z-N法整定PID参数的步骤与技巧，并对比其他整定方法，从而帮助读者全面理解Z-N法及其在现代自动化控制中的重要性。

# 2. PID控制理论基础

在这一章节中，我们将深入探讨PID控制器的工作原理，以及如何通过调整PID参数来优化控制系统的性能。PID控制理论是自动控制系统领域的基石，几乎在每一个控制环路中都可以见到它的身影。我们将逐步解构PID，分析其比例（P）、积分（I）、微分（D）三个部分的作用，以及它们是如何构成PID控制方程的。

## 2.1 PID控制器的工作原理

PID控制器是一种广泛使用的反馈控制器，它通过计算偏差或误差值（即期望输出与实际输出之间的差值）并对其进行比例、积分和微分处理，以此来调整控制输入，使得系统的输出尽可能接近期望值。

### 2.1.1 比例（P）、积分（I）、微分（D）的作用

- **比例（P）**：比例作用是PID控制器中最直接的控制方式，它的作用是根据当前的误差大小提供一个与之成比例的控制量。比例项可以立即反应误差大小，并试图纠正它。但是，比例控制并不能消除稳态误差。

- **积分（I）**：积分项是对误差进行积分，它能够随着时间的推移累积误差，并基于累积误差调整控制量。积分作用有助于消除系统的稳态误差，但可能会增加系统超调和振荡的风险。

- **微分（D）**：微分项对误差的变化率进行计算，它能够预测误差的未来趋势，从而提前进行控制。微分控制能够减小系统的超调和振荡，但对噪声非常敏感。

### 2.1.2 PID控制方程的构成

PID控制方程将P、I和D三个部分整合起来，以提供一个综合的控制量：

u(t) = K_p e(t) + K_i \int_{0}^{t} e(\tau) d\tau + K_d \frac{de(t)}{dt}

其中，`u(t)` 是控制输入，`e(t)` 是误差，`K_p` 是比例增益，`K_i` 是积分增益，`K_d` 是微分增益。通过调节这三个参数，可以实现对系统动态响应的精确控制。

## 2.2 PID参数对系统性能的影响

要实现良好的控制效果，正确地调整PID参数至关重要。PID参数的选择将直接影响系统的稳定性、响应速度和准确度。

### 2.2.1 增益对系统稳定性的影响

增益在PID控制器中分别对应于比例、积分和微分参数。这些参数不仅影响系统的稳定性，还影响其对扰动的反应能力和系统的动态性能。

- **比例增益**：增加比例增益可以提升系统对误差的响应速度，但过高会导致系统过度振荡甚至不稳定。
- **积分增益**：积分增益的增加有助于消除稳态误差，但同时会减慢系统的响应速度，并可能引起系统振荡。
- **微分增益**：微分增益主要用来改善系统的阻尼特性，减少超调，但过高的微分增益会使系统对噪声过于敏感。

### 2.2.2 参数调整与系统响应速度的关系

参数调整是控制系统设计中的一个关键过程。理想情况下，我们希望系统的响应既快又平稳，这通常需要通过试验和调试来实现。

- **快速响应**：如果系统需要快速达到设定点，可能需要提高比例增益，同时需要确保积分和微分增益不会导致系统不稳定。
- **平稳过渡**：为了减少或消除振荡，可以适当增加微分增益以提高系统的阻尼比。同时，调整积分增益可以帮助系统快速消除稳态误