Z-N法整定PID参数的模拟与仿真：软件工具的专家使用指南


# 摘要
本文全面探讨了Ziegler-Nichols（Z-N）法在PID参数整定中的应用，包括理论基础、整定原理、仿真软件操作，以及模拟与仿真的高级技巧。通过阐述控制系统稳定性、PID控制器的组成及Z-N法的基本原则，本文详细介绍了Z-N法整定的步骤和在实践中可能遇到的问题及解决对策。文章还深入分析了仿真软件工具的选用、环境搭建和仿真结果分析。此外，本文提供了针对特定条件下的PID参数调整技巧，并通过工业控制案例分析，展示了这些技术在实际应用中的价值。最后，探讨了高级控制策略、仿真工具的高级功能和专家系统在PID整定中的应用，为提高控制系统的性能和可靠性提供了新的视角。

# 关键字
Z-N法；PID参数；控制系统；仿真软件；稳定性分析；工业控制

参考资源链接：[Z-N法整定PID参数经验分享](https://wenku.csdn.net/doc/6412b793be7fbd1778d4acb6?spm=1055.2635.3001.10343)
# 1. Z-N法整定PID参数的理论基础

在深入探讨Ziegler-Nichols（Z-N）法整定PID参数的实际应用之前，本章将首先介绍PID控制系统的理论基础，为读者提供一个清晰的背景知识框架。我们将从控制系统稳定性的基本概念开始，然后介绍PID控制器的作用和组成部分，最后阐述Z-N法整定的基本原则。这些理论基础将为后续章节中更复杂的应用和优化技巧提供坚实的支撑。

## 1.1 控制系统稳定性的基本概念

控制系统稳定性是评价系统性能的关键因素之一。一个稳定的系统能在受到扰动后最终回到平衡状态，而不会产生无限增长的振荡或偏差。为了确保系统稳定，工程师通常使用数学模型来分析和预测系统的响应特性，这包括系统的阶跃响应、频率响应等。

## 1.2 PID控制器的作用和组成

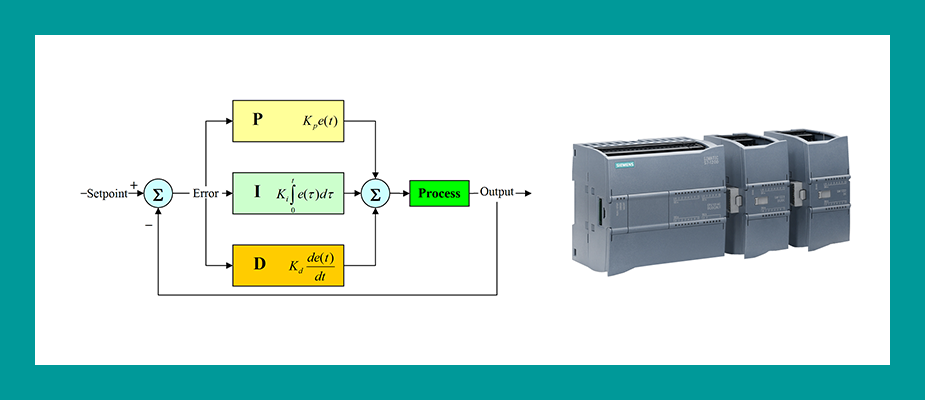
PID控制器是一种广泛使用的反馈控制器，它的名称来自于比例（P）、积分（I）和微分（D）三个控制动作。这三个控制动作共同工作以减小系统的误差。比例项负责当前误差的响应，积分项处理误差的累积影响，而微分项则预测误差的趋势。每个组成部分在控制器中扮演着不同的角色，共同维持系统的稳定性。

## 1.3 Z-N法整定的基本原则

Z-N法是一种经验性的PID参数整定方法，其核心在于依据系统的临界振荡条件来快速确定PID参数。该方法通过两步简单的实验操作来获取临界增益和临界振荡周期，然后使用这些数据和预先定义的经验公式直接计算出比例、积分、微分三个参数的值。Z-N法因其简单性和实用性在工业应用中非常受欢迎。

# 2. Z-N法整定PID参数的原理与步骤

## 2.1 Z-N法整定PID控制器参数的理论框架
### 2.1.1 控制系统稳定性的基本概念

控制系统稳定性是控制理论中的核心概念，它指的是系统在受到扰动或初始条件变化后能否回到平衡状态的能力。稳定性分析通常涉及到系统内部的动态行为，以及其对控制输入的响应。在数学上，一个线性时不变系统（LTI系统）是稳定的，如果其所有特征根都位于复平面的左半平面。

在应用Ziegler-Nichols (Z-N) 方法时，我们假设系统可以近似为一阶加延时（First Order Plus Dead Time，FOPDT）模型。这意味着系统响应可以用时间常数（τ）、增益（K）和延迟时间（θ）三个参数来描述。Z-N方法利用这一模型，通过观测系统的开环响应来整定PID参数，使控制器能够在保证系统稳定的同时，达到期望的性能。

### 2.1.2 PID控制器的作用和组成

PID控制器由比例（Proportional）、积分（Integral）、微分（Derivative）三个基本控制动作构成。每个动作都有其特定的功能：

- **比例（P）**：响应当前的偏差。较大的比例增益可以使系统响应更快，但也可能引入振荡。
- **积分（I）**：消除稳态误差。积分作用能累计过去的偏差，适用于消除长期偏差。
- **微分（D）**：预测未来偏差的趋势。微分控制能够对系统即将发生的偏差做出反应。

### 2.1.3 Z-N法整定的基本原则

Z-N法是一种基于实验的方法，它提供了两套不同整定规则，分别对应于纯比例控制（P控制）和比例-积分控制（PI控制）。Z-N法的基本原则是首先让闭环系统在纯比例控制下稳定运行，然后逐渐增加比例增益直到系统达到临界稳定状态。这个临界状态可以通过观察系统响应的振荡来识别，此时记录下临界增益（Kc）和临界周期（Tc）。

在Z-N的P控制规则中，推荐的PID参数计算公式如下：

- 比例增益（Kp）= 0.6 * Kc
- 积分时间（Ti）= Tc / 2
- 微分时间（Td）= Tc / 8

而在PI控制规则下，参数为：

- 比例增益（Kp）= 0.45 * Kc
- 积分时间（Ti）= Tc / 1.2
- 微分时间保持为零，因此这是一个PI控制器。

## 2.2 Z-N法整定的具体步骤

### 2.2.1 手动整定过程的初步参数获取

在使用Z-N法进行PID参数整定之前，首先需要进行手动测试来获取初步参数。以下是获取初步参数的步骤：

1. **设置控制器为P控制模式**，并从一个较小的比例增益开始。
2. **逐渐增加增益**直到系统开始振荡。
3. **记录此时的增益值**，这是临界增益（Ku）。
4. **测量振荡周期**，得到临界周期（Tu）。
5. 使用这些数据来根据Z-N公式计算出初始的PID参数。

### 2.2.2 根据系统响应曲线确定PID参数

在初步参数获取之后，接下来会根据系统的响应曲线调整PID参数。响应曲线通常是由阶跃响应得出的，其中包含了系统对阶跃输入的反应信息。通过分析响应曲线可以确定系统类型和动态特性，进而微调PID参数。需要关注的关键点包括：

- 系统达到稳态的时间
- 系统振荡的幅度和频率
- 系统是否存在延迟
- 稳态误差的大小

根据这些特性调整PID参数，可以使系统更快地达到稳态，减少振荡，消除稳态误差。

### 2.2.3 参数调整和验证

参数调整之后，必须进行实际的验证来确保系统性能满足要求。这通常通过以下步骤进行：

1. **实施新的PID参数**，并让系统运行一段时间。
2. **观察系统对扰动和负载变化的反应**，确保系统稳定且响应时间合理。
3. **收集系统运行数据**，包括误差、振荡频率等关键性能指标。
4. **根据实际运行情况**对PID参数进行微调，以达到最佳性能。

验证过程可能需要多次迭代，直到找到最佳的PID参数设置。

## 2.3 Z-N法整定中的问题与对策

### 2.3.1 过度调谐和振荡问题

过度调谐是指系统对输入变化或扰动反应过于激烈，导致振荡加剧。解决这一问题的一种方法是降低比例增益或增加积分时间。在Z-N方法中，可以通过减少按照Z-N公式计算出的Kp值来减小比例控制的作用，或者增加积分控制的时间常数（Ti）。

### 2.3.2 控制系统的延迟和非线性问题

当控制系统存在延迟或非线性特性时，Z-N方法可能无法提供满意的整定结果。例如，系统的响应可能不是典型的指数衰减形式，或者存在死区、饱和等非线性因素。在这种情况下，可以使用更加复杂的模型或调整方法，如模型预测控制（MPC）或基于规则的方法。

### 2.3.3 应用实例分析

应用实例分析是验证Z-N方法有效性的重要手段。通过选择具有代表性的应用案例，将Z-N方法应用于实际系统，并观察系统的性能变化。案例分析可以帮助工程师了解Z-N方法在特定条件下的适用性，并针对具体问题进行参数调整。这样的分析不仅可以提供解决方案，还能够帮助工程师建立对Z-N方法的直觉理解。

# 3. 仿真软件工具的介绍和操作

在自动化控制系统的设计与优化过程中，使用仿真软件工具进行模拟是不可或缺的环节。仿真可以帮助设计人员在不进行实际物理系统搭建的情况下，测试和验证控制策略的有效性。本章将详细介绍选择、安装、构建仿真环境、分析仿真结果以及调整仿真参数的方法。

## 3.1 仿真软件工具的选择与安装

### 3.1.1 常用仿真软件的对比和选择

在选择仿真软件时，应考虑其功能的完整性、用户界面的友好性、模型的准确性以及支持的算法范围。常见的一些仿真软件包括MATLAB/Simulink、LabVIEW、Modelica等。MATLAB/Simulink以其强大的数学计算和灵活的模型设计功能，在学术和工程领域拥有广泛的应用。LabVIEW提供了丰富的硬件接口，便于控制系统和测量设备的集成。Modelica作为面向对象的物理建模语言，非常适合于复杂的多领域仿真。

### 3.1.2 软件的安装与环境配置

以MATLAB/Simulink为例，安装过程通常包括下载安